A legnagyobb lejtő vonala
A legnagyobb meredekség vonala egy vízszintes síkra merőleges egyenes. L.N.S. a sík dőlésszögének meghatározására szolgál a π1 - α nyúlványok síkjára (58. és 59. ábra). Az AB-vonal a legnagyobb meredekség. A'B'ψhoαα az AB π1 dőlésszögének szöge. Ez a vízszintes vetület és az AB szegmens természetes értéke közötti szög.
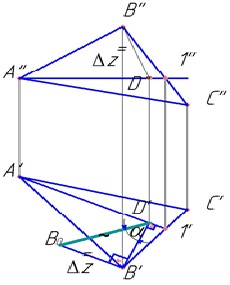
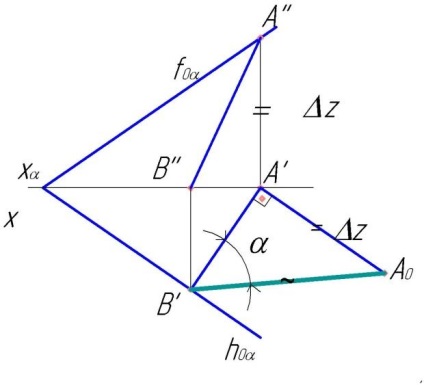
Határozza meg az AB szegmens valós értékét. A vízszintes vetületen egy jobb háromszöget építünk fel az A'B 'és a Δz lábakkal. Az a szegmens a valós érték és az AB szegmens vízszintes vetülete között a sík dőlésszögének a vetületek vízszintes síkjához viszonyított szöge.
Az 58. ábra mutatja az LNS konstrukcióját. BD.
A Δ ABC tartott vízszintes A1 és bármely pontjáról a sík (a példában (∙) tartott L.N.S. BD (B'D „┴A'1”) szög α -. Az ABC háromszög szög a vízszintes síkkal vetítési .
Két sík metszésvonalának megépítése
Két sík mindig egyenes vonalban metszik egymást. A keresztezési vonal megépítéséhez elegendő megtalálni a vonal két pontját, vagy egy pontot és ennek a vonalnak a irányát. Tekintsünk több esetben a síkok metszéspontjaira.
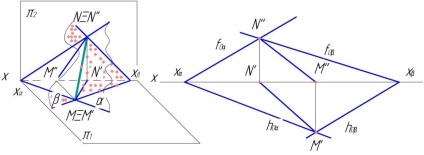
1. példa Az α és γ két sík egyenes vonalú MN vonalban (60. Ábra) metszi a rajz határán belül.
2. példa Két sík metszéspontja vízszintesen (vagy frontálisan) történik.
A 61. és 62. ábrákon a metszetvonal elülső vetülete egybeesik az f0γ nyomával. és a vízszintes a vízszintes vízszintes vetületeként jelenik meg ebben a síkban.
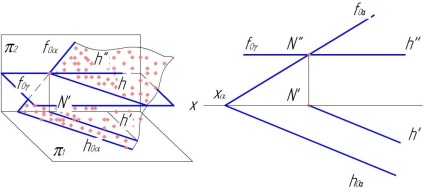
3. példa A rajzon belül az α és β síkok két vízszintes sávja metszi egymást (63.
Megtaláljuk az M pontot a vízszintes nyomok metszéspontjában. Az N pont megtalálásához további kiegészítő vízszintes síkot γ kell venni. Ez a szekvencia sík az a és β síkokat metszi a horizontális síkon. Ezeknek a kontúroknak a metszéspontjában lévő vízszintes vetülete adja az α és β síkok metszéspontjának második pontját - az N pontot (64.
4. példa Egy síkot általános pozíció nyomvonalak adnak meg, a második síkot két, általános helyzetű metszésvonal adta (65. ábra).
1. Az adott pozíció kiegészítő síkját rajzoljuk, például a vízszintes sík síkját β || π1 (fòβ || x) (66.
2. A sík β metszi a síkot a vízszintesen h.h "

3. A sík β metszi az (a∩b) síkot az egyenes vonal mentén (2-3).
4. A h és a 2-3 vonalak metszi az M pontot (M 'és M' '). ahol M '= h'∩ (2'-3') és M "

5. A második közös pont megalkotásához egy másik γ || π1 (fòγ || x) kiegészítő síkot rajzolunk (67.
6. A sík γ metszi a síkot a vízszintesen h1: h1 "

7. A sík γ metszi az (a∩b) síkot egy egyenes vonal mentén (5-6).
8. A h1 és az 5-6 vonalak metszenek az M (M "és M ') ponton. ahol M '= (5'-6') ∩h1 ', M "

9. Az azonos nevű vetületeket M és N kapcsoljuk össze, és a metszésvonal (M'N ') és (M'N') vetületét kapjuk.
5. példa Egy adott pozíció ΔABC síkja (ΔABC
ΔABC óta
1. Az ABC és az MNK háromszögek vízszintes vetületeinek metszéspontján a Q 'és T' általános vízszintes vetületeket jegyezzük meg (69.
2. Keressük a frontális Q '' és T '' nyúlványokat a metszésvonal vonalán a ΔM''N''K'''-ben.
3. A QT keresztezési vonalat QT (Q''T '' és Q'T ') határozza meg.
4. Határozza meg a síkszámok láthatóságát, t. a repülőgépek átlátszatlanok. A számok vízszintes vetületének láthatóságát nem kell meghatározni, mert A ΔABC egyenes vonalban van vetítve, az M'N'K 'vetítés látható. Meghatározzuk a síkképek láthatóságát a π2 vetületek síkjához viszonyítva. Ehhez vegye figyelembe a BC és az MK egymást keresztező vonalakon fekvő 1. és 2. pontokat. Az 1 "és 2" homlokfelületek egybe esnek, és a vízszintes 2 'vetület az 1' vízszintes vetület előtt van. Az 1 "pont láthatatlan a π2 vetületek síkjához képest. Továbbá az alábbiak szerint vitatjuk: a 2. pont a ΔABC-ra oszlik. következésképpen a ΔA''B''C "elülső kivetítés látható a π2-en az oldalról, ahol az 1" és 2 "pontok találhatók. A Q "és T" keresztezési vonal frontális vetülete után a ΔA''B''C "láthatósága az ellenkező irányba változik, azaz a láthatatlanná válik (69.