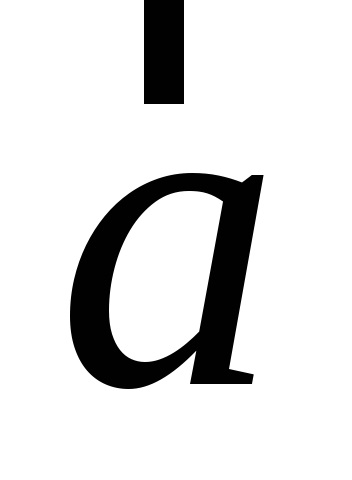A vetítés a vektor a tengelyen

Tengely az úgynevezett irányított vonal.

Meghatározás. Orth tengely

Ez az úgynevezett egység vektor, amelynek iránya egybeesik a tengely irányában.

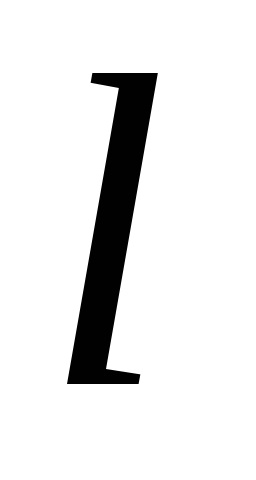
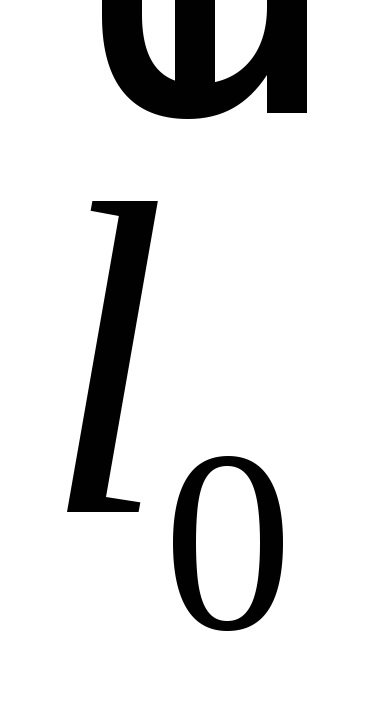
Meghatározás. A merőleges vetülete M a tengellyel

nevezett adatbázis M1 merőleges a M .

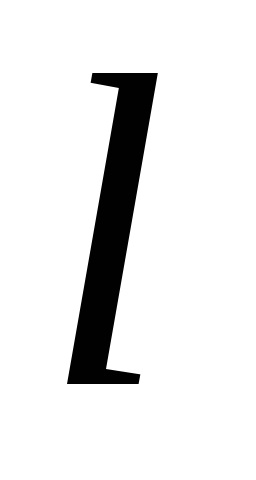
Meghatározás. Ortogonalnoyproektsiey vektor

tengelynazyvaetsyadlina szegmens A1 B1 e tengely, között kötött ortogonális vetülete annak elején és végén, venni a „+” jel, ha az irányvektor Ez egybeesik a tengely irányában, és a „-” jel, ha az irányok ellentétes (8. ábra).

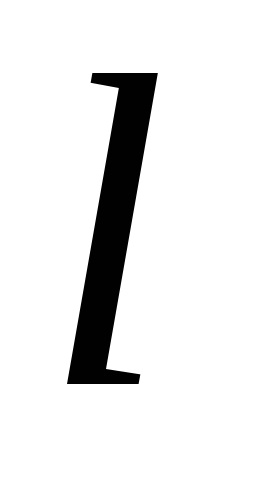
Meghatározás. A szög a vektor és a tengely a szög, ahol el szeretné forgatni a pozitív irányú a tengelye fedésbe az irányt a vektor irányát (pozitív tekinthető óramutató járásával ellentétes irányban).

Nyilvánvaló, hogy a nyúlvány a vektor a tengelyen található, amelyet a képlet

Belátható, hogy a nyúlvány egy lineáris kombinációja vektorok az azonos lineáris kombinációja az előrejelzések:

.

Különösen, a nyúlvány a vektor összege egyenlő az összegével előrejelzések:

.

Vegyünk egy Descartes-féle derékszögű koordináta-rendszer HOY. jelent

- az egység vektor az x tengely,- ort osiOY. Válasszon egy pontot , és hagyja- előrejelzések azt OX örömeit, azaz a koordinátái e pont (9. ábra).

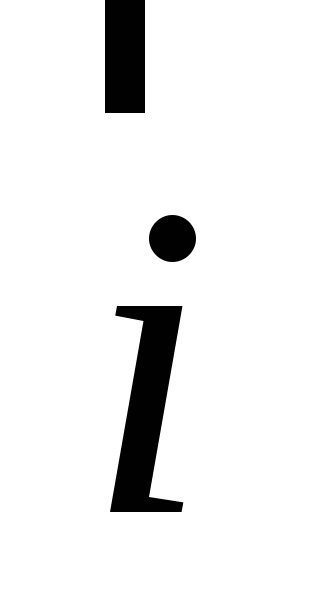
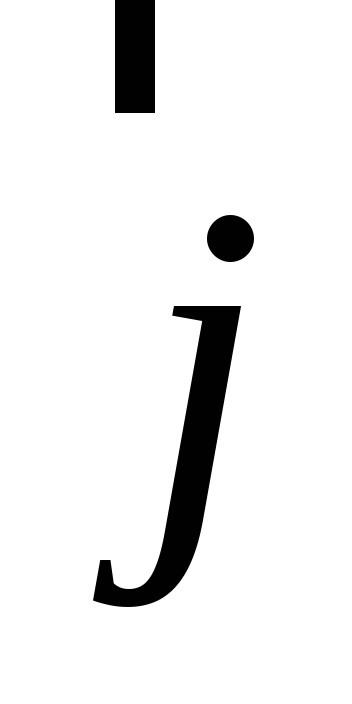
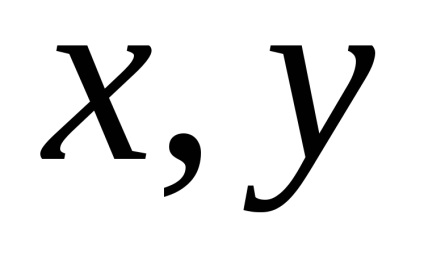
Így, ha egy adott Descartes-féle derékszögű koordináta-rendszer (pdsk), az összes térbeli vektor

összekapcsolhatja a három szám(Vagy két szám, Ha a vektor lapos), amelyek a hőtágulási együtthatók a vektor alapján vektorok a koordinátatengelyek, valamint a nyúlványok a vektor a koordinátatengelyeken.

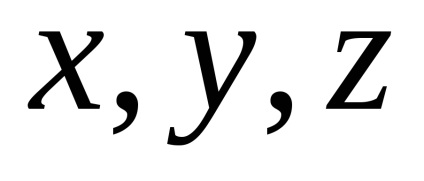
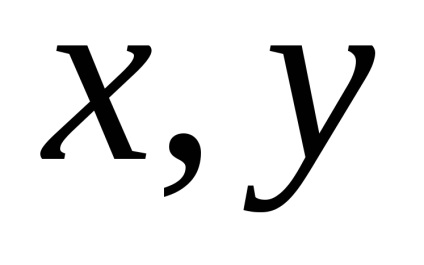
Meghatározás. koordináták vektor

a lyuboypdsk úgynevezett koefficiensek bővítése a vektor az egység vektorok a koordinátatengelyek.

Így tudjuk adni egy másik definíciót a vektor.

Meghatározás. Egy vektor egy rendezett hármas számok (egy rendezett pár, ha a vektor lapos).

Példa. Ha, akkor

= (2,3,4), és fordítva, ha, az

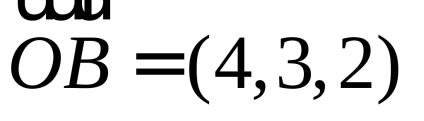
Mivel, egyrészt, a vektor - a tárgy, amelynek hossza és iránya, és a másik, - egy rendezett hármas számok, ismerve a hossza és iránya, az egyik tudja határozni saját helyzetét, és fordítva. Az irányvektor egy előre meghatározott koordináta-rendszerben, azzal jellemezve, hogy annak iránykoszinuszokat (11. ábra):

.

Kapcsolódó cikkek

• A dot termék két vektor, skaláris szorzata két merőleges vektor

• Az állam, vektor - fizikai enciklopédia

• A vektor a jelenlegi állapot