Know-how, előadás, adatfolyamkódok és pszeudo-véletlenszám-generátorok
Pszeudo-véletlenszám-generátor a BBS algoritmus alapján
Minden egyes n-edik lépésben a generátor számítjuk xn + 1 = xn 2 mod M. Az eredmény n-edik lépésben az egyik (általában kisebb) bitjeit xn + 1. Néha a paritásbitet használják az eredménynek, vagyis az elem bináris ábrázolásában lévő egységek számát. Ha a számbevitelben lévő egységek száma egyenletes, a paritásbitet 0-ra állítjuk. Páratlan - a paritás bit értéke 1.
Például. legyen p = 11, q = 19 (meggyőződésünk, hogy 11 mod 4 = 3, 19 mod 4 = 3). M = p * q = 11 * 19 = 209. Válassza az x értéket. viszonylag elsődleges az M. számára. Legyen x = 3. Számítsuk ki az x0 generátor kezdőszámát:
Az első tíz xi számot a BBS algoritmussal számoljuk ki. Véletlen bitekként az xi szám bináris ábrázolásában a legkevésbé jelentős bitet veszünk:
Ennek a módszernek az a legérdekesebb gyakorlati célja, hogy a szekvencia n-edik számának megszerzéséhez nem szükséges minden előző x számot kiszámítani. Kiderül, hogy az xn azonnal kapható a képletből
Például az x10-et x0-ből egyszerre kiszámíthatja:
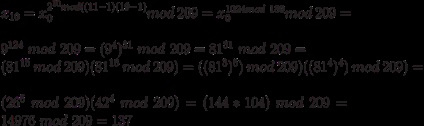
Ennek eredményeképpen tényleg ugyanaz az érték. mint a szekvenciális számításnál, 137. A számítások meglehetősen bonyolultnak tűnnek, de valójában könnyű formalizálni őket egy kis eljárás vagy program formájában, és szükség esetén felhasználják.
Lehetőség „közvetlen” vétel xn lehetővé teszi a használatát egy algoritmus BBS stream titkosítás, például véletlen hozzáférésű fájlokat vagy töredékek adatbázis bejegyzéseivel.
A BBS algoritmusának biztonsága azon a bonyolultságon alapszik, hogy nagyszámú M-t bontanak többszörösre. Azt állítják, hogy ha M elég nagy, akkor sem lehet titokban tartani; addig, amíg az M nem faktorizálódik, senki sem képes előre megjósolni a PSC generátor kimenetét. Ez annak a ténynek köszönhető, hogy a probléma a bomlás számok formájában n = pq (p és q - prímszám) faktorizációs számításigényes nagyon nehéz, ha csak annyit tudunk, n. és p és q nagyszámú, több tíz vagy száz bitből áll (ez az úgynevezett faktorizációs probléma).
Ezenkívül bizonyítani tudja, hogy a támadó. ismerte a BBS generátor által generált sorozatokat. Nem tudja meghatározni sem az előző biteket, sem a következőket. A BBS generátor bal és jobb irányba megjósolhatatlan. Ez a tulajdonság nagyon hasznos kriptográfiai célokra, és összefüggésben van az M. szám faktorizálásának szingularitásával.
A legjelentősebb hátránya az algoritmus, hogy ez nem elég gyors, hogy nem teszi lehetővé, hogy használni számos területen, például a számítások valós időben, valamint, sajnos, és streaming titkosítást.
De valóban ez az algoritmus ad jó pszeudo-véletlenszám-szekvencia hosszú ideig (a megfelelő választás a kezdő paraméterek), amely felhasználható kriptográfiai célra a generációs titkosítási kulcsokat.
Kulcsfogalmak
A stream kódolás egy stream kód.
A pszeudo-véletlenszám-generátor (GPRS) egy olyan algoritmus vagy eszköz, amely olyan bitek sorozatát hozza létre, amelyek véletlenszerűnek tűnnek.
Lineáris kongruencia véletlenszám-generátor - egy egyszerű PRNG amely kiszámításához a következő szám Ki használja a Ki = (a * Ki-1 + b) mod c. ahol a, b, c állandók. a ki-1 az előző pszeudo-véletlenszám.
A Fibonacci-retardált módszer a pszeudo-véletlen számok előállításának egyik módja. Fel lehet használni kriptográfiában.
A stream kódoló egy kód. amely műveletenként egy bit (vagy byte) bemeneti üzenet titkosítását végzi. A streaming titkosítási algoritmus kiküszöböli annak szükségességét, hogy az üzenetet egész számú blokkra osztja. Az adatfolyam titkosításait valós időben titkosítják.
Összefoglaló eredmények
A stream kódoló egy kód. amely műveletenként egy bit (vagy byte) bemeneti üzenet titkosítását végzi. A streaming titkosítási algoritmus kiküszöböli annak szükségességét, hogy az üzenetet egész számú blokkra osztja. Így, ha egy karakterfolyamot továbbítanak, akkor minden karakter titkosítva és azonnal továbbítható. Az adatfolyam titkosításait valós időben titkosítják.
Az áramforgalmazók kulcsainak generátoraként pszeudo-véletlenszám-generátorok (GPRS) használhatók. A GPRS használatának célja, hogy "végtelen" kulcsszót kapjon, viszonylag kis hossza a kulcsnak. Céljára használható kriptográfiai álvéletlen szám-generátor kell rendelkezniük bizonyos tulajdonságai, például szekvencia időszak által generált oszcillátor legyen nagyon magas.
A pszeudo-véletlen számok legegyszerűbb generátorai: egy lineáris kongruenciális generátor. generátor a késleltetett Fibonacci-módszerrel, generátor a Blum-Blum-Shuba algoritmus (BBS) alapján.
Állítsa be a gyakorlatot
Kérdések önvizsgálatra
- Hogyan változik az adatfolyam-kód a blokk-titkosítástól?
- Hogyan szerveződik a változó hosszúságú adatfolyam titkosítása?
- Milyen számokat neveznek "pszeudorandomnak"?
- Milyen tulajdonságokkal rendelkezik a pszeudo-véletlenszám-generátor titkosítási célokra?
- Milyen pszeudo-véletlenszám-generátorokat tudsz megnevezni?
- Sorolja fel az előadásban szereplő összes pszeudo-véletlenszám-generátor fő jellemzőit, előnyeit és hátrányait.
Gyakorlatok önvizsgálatra
- Határozzuk meg az első tíz szám sorrendjét és a lineáris egybefüggő generátor PSC időtartamát különböző a, b és c paraméterekhez (k0 0-nak vesszük):
- a = 5, b = 7 és c = 17;
- a = 6, b = 3 és c = 23.
- a = 3, b = 1, k0 = 0,6; k1 = 0,3; k2 = 0,5;
- a = 4, b = 2, k0 = 0,9; k1 = 0,3; k2 = 0,5; k3 = 0,9.