Megfelelőségi koncepció
Kezdetben az algebra az egyenletek megoldásának elmélete volt. A fejlődés sok évszázadán át az algebra olyan tudománysá vált, amely tanulmányozza a műveletek és kapcsolatok különböző készleteiben. Ezért nem véletlen, hogy az általános iskolában a gyerekek megtanulják algebrai fogalmak, mint a véleménynyilvánítás (numerikus és változó), a numerikus egyenlőség, numerikus egyenlőtlenség egyenlet. Tanulmányozzák a számtani műveletek különböző tulajdonságait olyan számokon, amelyek lehetővé teszik a számítások racionális végrehajtását. És persze, egy kezdeti során matematika ezek ismerete különféle függőségek, a kapcsolatok, de használni őket a fejlesztési szellemi tevékenység a gyermekek, a tanár rendelkeznie kell néhány általános fogalmak a modern algebra - megfelelő koncepció, magatartása, algebrai műveletek, stb Ezen kívül ,. tanulás a matematika nyelvén, használt algebra, a tanár képes lesz, hogy jobban megértsék a természet matematikai modellezése valós jelenségek és folyamatok.
A körülöttünk levő világ tanulmányozása során a matematika nemcsak a tárgyakat vizsgálja, hanem elsősorban a köztük levő kapcsolatokat. Ezeket a kapcsolatokat függőségeknek, összefüggéseknek, kapcsolatoknak, függvényeknek nevezik. Például az objektumok hosszának kiszámításánál vannak objektumok és számok közötti megfeleltetések, amelyek hosszúságuk értékei; amikor a mozgás problémáinak megoldása esetén a megtett távolság és az idő közötti kapcsolat létrejön, ha a mozgás sebessége állandó.
A matematika tárgyaitól függõ függõségek, megfelelések, összefüggések tanulmányozása kezdete óta. De a kérdés, hogy milyen közösek a különböző levelezések, mi a lényege bármilyen levelezés volt a posztot a 19. század végén - a 20. század elején, és a választ találtak a keret elmélete keretében.
A matematika kezdeti szakaszában különböző, egy, két vagy több elem elemei közötti kapcsolatokat vizsgálnak. Ezért a tanárnak meg kell értenie a lényegét, ami segít neki abban, hogy biztosítsa az egységet az ilyen kapcsolatok tanulmányozásának módszertanában.
Tekintsünk három példát a matematika kezdeti tanulásakor vizsgált megfelelésekre.
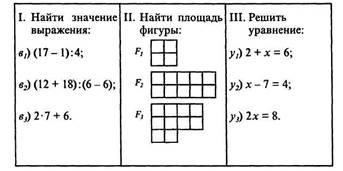
Az első esetben az adott kifejezések és azok számértékek közötti megfelelést hozunk létre. A másodikban meghatároztuk, hogy melyik szám megfelel ezeknek a számoknak, amelyek jellemzik a területét. A harmadikban olyan számot keresünk, amely az egyenlet megoldása.
Milyen közösségek vannak ezeken a levelezéseken?
Látjuk, hogy minden esetben van két: az első - egy három numerikus kifejezéseket és a beállított N a természetes számok (ő tulajdonában kifejezést adat értékek), a második - egy három geometriai alakzatok és a beállított N a természetes számok; a harmadik pedig három egyenlet és a természetes számok N csoportja.
A javasolt feladatok végrehajtása során létrehozunk egy kapcsolatot (levelezést) ezen készletek elemei között. Grafikailag látható (1.
Megadhatja ezeket a megfeleltetéseket, ha felsorolja a megadott mérkőzésen található összes elempárt:
A kapott készletek azt mutatják, hogy az X és Y csoportok közötti bármilyen megfelelés rendezett párok sorának tekinthető. elemekből. És mivel a rendezett párok a Descartes-termék elemei, a következő általános definíciót érjük el.
Definíció. Az elemek közötti megfelelésnél az X és Y halmaz az e készletek Descartes termékének bármelyik részhalmaza.
A levelezést általában P, S, T, R stb. Betűkkel jelöljük. Ha S az X és Y készlet elemeinek megfeleltetése, akkor definíció szerint S x x Y.
Most magyarázzuk meg, hogyan határozzák meg a két csoport közötti kapcsolatokat. Mivel a levelezés egy részhalmaz, bármely csoportot definiálhatjuk, vagyis bármely csoportot. vagy a megadott levelezésben lévő összes elempár számozásával, vagy a részhalmaz elemeinek jellemző tulajdonságának megadásával. Így meghatározható az X = és Y = halmazok közötti megfelelés:
1) kétváltozós mondattal: a
2) a Descartes-termék XxY részhalmazához tartozó számpárok felsorolása: A hozzárendeléshez ezt a módszert is hozzárendeljük egy összefüggéshez (2. ábra) és egy grafikon segítségével (3. ábra)
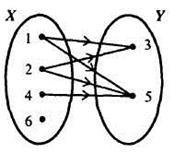
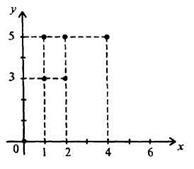
Gyakran az X és Y készlet elemei közötti megfelelés tanulmányozása, a másolás ellenére is figyelembe kell venni. Tegyük fel például,
S - levelezés "több mint 2" a készletelemek között
X = és Y =. Ezután S = és a grafikonja megegyezik a 4a.
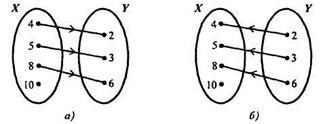
A levelezés, ennek ellentéte a "kevesebb 2-nél". Az Y és X készlet elemei között figyelembe vesszük, és grafikusan ábrázoljuk, elegendő az S arány grafikonján lévő nyilak irányát megváltoztatni (4b. Ábra). Ha a "kevesebb, mint 2" levelezés S-1-nek nevezik. akkor S -1 =.
Egyetértünk azzal, hogy az "x elem az S elemnek az y elemével" kifejezését röviden, mint xSy írja. Az xSy jelölés a konkrét megfeleltetések feljegyzéseinek generalizálásaként tekinthető: x = 2y; x> 3y + 1 és mások.
A beírt rekordot használjuk, hogy meghatározzuk a levelezés inverz fogalmát.
Definíció. Legyen S az X és Y halmaz elemei közötti megfelelés. Az Y és X készletek elemei között az S -1 megfeleltetést fordítottnak nevezzük, ha yS -x, ha és csak akkor, ha xSy.
Az S és S -1 illesztéseket egymásnak inverznek nevezzük. Lássuk a grafikonok jellemzőit.
Legyen az S = (5a. Ábra) összefüggési grafikon. Az S -1 illesztési grafikon létrehozásakor meg kell választanunk az első komponenst az Y =, és a második az X = halmazból. Ennek eredményeképpen az S-1 illesztési grafikon egybeesik a S levelezés grafikonjával. Az S és S-1 illesztések grafikonainak megkülönböztetése érdekében,
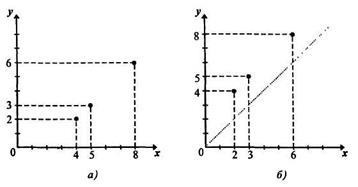
Az S -1 levelezőpár első komponense az abszcissza, a második pedig az ordinát. Például, ha (5, 3) S, akkor (3, 5) S -1. A pontok koordinátái (5, 3) és a (3, 5), és általában (x, y) és (y, x) szimmetrikus a felezővonal a 1. és 3. negyedre. Ezért, grafikák kölcsönösen inverz megfelelések S és S -1 szimmetrikus a felezővonal a 1. és 3. negyedre.
Az S -1 levelezés grafikájának megrajzolása. elegendõ olyan pontokat ábrázolni a koordináta síkon, amelyek szimmetrikusak az S gráf pontjaihoz képest az 1. és 3. koordináta szögek felsõ részére.