A holonomiai rendszerek
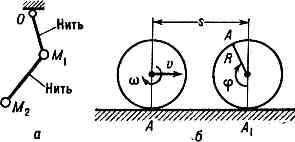
mechanikusan. rendszerek, ahol minden link (lásd COMMUNICATIONS MECHANICAL) yavl. geometrikus (holonomikus), amely csak a rendszer pontjai és testeinek pozícióira (vagy mozdulatok mozgása során) korlátozza, de nem a sebességük nagyságára. Például. kettős inga (a ábra) yavl. G. sz. ben, a csatlakozások (húrok) csak az M1 és M2 rakományok helyzetét vagy mozgását korlátozzák, de nem a sebességükön, ami mozgáskor bármilyen értékkel bírhat. Az a kényszer, amely korlátozza a rendszer pontjai és szervei sebességét, vagyis meghatározza ezeket a sebességeket, kapcsolat, n. kinematikai. Ha azonban ezek a kapcsolatok geometriai, azaz a rendszer pontjai és testeinek elmozdulása (vagy koordinátái) közötti kapcsolatra korlátozódnak, akkor ez a kapcsolat is. holonomic. Például. amikor egy R sugarú kerék görgője egyenes vonalú sín mentén (b. ábra), csúszás nélkül, a kerék középpontjának v sebességét és a szöget. A kerék sebességének sebességét a v = Rw reláció határozza meg, de lecsökkenthető egy geomra. a középpont s = AA1 elmozdulása és a kerék forgási szöge j közötti relatív s = Rj. Ezért ez G. a.
Kinematikai. Azok a kapcsolatok, amelyek nem csökkentik a geometriaiakat, nevezik. nem holonomikus és mechanikus. ilyen összeköttetésekkel rendelkező rendszerek - nem holonomikus rendszerek. Mechanikai elválasztás. rendszerek holonomic és nonholonomic nagyon fontos, hogy van. Hogy. száma ur-CIÓ teszi, hogy viszonylag könnyű megoldani a problémákat, a mechanika (vö. Lagrange-egyenletek a mechanika), csak a gs.
Nézd meg, mi a "GOLON" más szótárakban:
Holonomic rendszerek - a mechanikai rendszert, amelyben minden kommunikáció (. Cm mechanikus kapcsolat) geometriai (holonomic), vagyis, hogy korlátozásokat csak a helyzet (vagy elmozdulás mozgás közben) pontok és szervek a rendszer, de nem az értéke a ... ... Nagy Szovjet enciklopédia
Nonholonomic rendszerek - a mechanikai rendszert, amely azon túlmenően, hogy a geometriai, kinematikai megszorításoknak több, nem lehet csökkenteni geometriai és nevezett holonomic (lásd Holonomic rendszerek.). Példa a N. s. Ez egy labda gördülés nélkül csúszik ... A nagy szovjet enciklopédia
NON-HYBRID RENDSZEREK - mechanikus. Olyan rendszerek, amelyek a geometriaiak mellett még mindig kinematikussá válnak. Olyan kapcsolatok, amelyek nem csökkentik a geometriai és nem holonomikus (lásd a GLONOM SYSTEMS-t). N. példa a. Egy labda gördül, anélkül, hogy csúszna egy durva síkon. Ugyanakkor ... ... Fizikai enciklopédia
MECHANIKAI CSATLAKOZÁSOK - a mechanikus helyzethez vagy mozgásokhoz kapcsolódó korlátozások. rendszer. Általában az SM-t a c.n. tel. Az ilyen SM felületekre példaként említhető, hogy a test csúszik vagy tekercsel; menet, amelyen a terhelés felfüggesztett; Csuklópántok, összekötő kapcsolatok ... ... Fizikai enciklopédia
Lagrange egyenlet - 1) egyenletek a mozgás fluid Yid Coy közegben rögzítik a Lagrange változók, amelyek a koordinátákat a részecskék a közegben. L.U. Határozza meg a részecskék mozgásának törvényét a közegben az idő koordinátái függvényében, és szerintük ... ... Nagy szovjet enciklopédia
A mechanikai összeköttetések a mechanikai rendszer helyzetére vagy mozgására vonatkozó korlátozások. Általában az SM-t bizonyos testek segítségével végzik. Példák erre az SM-re olyan felület, amely fölött a test csúszik vagy tekercsel; a szálat, amelyen a rakomány felfüggesztésre került; ... ... nagy szovjet enciklopédia
A szabadság fokozatai számozottak a mechanikában, a mechanikus rendszer független lehetséges elmozdulásainak számát (lásd a lehetséges mozgásokat). C. a. h) a rendszert alkotó anyagi részecskék számától és a rendszer által okozott kapcsolatok számától és jellegétől függ ... ... Nagy Szovjet Encyclopedia
Poincaré egyenletek - általános egyenletei mechanika holonomic rendszerek leírható segítségével egy bizonyos Roy Lee csoport infinitezimális transzformációk. Legyen x i, i = 1. n, olyan változók, amelyek meghatározzák a holonomikus szerelő pozícióját. rendszer, melyet az ideális kapcsolatok kényszerítenek, ... ... Matematikai Encyclopedia
Holonomic megszorítások - holonomic mechanikus kapcsoló tag, amely korlátozásokat csak a helyzet (vagy elmozdulás) pontok és szervek a rendszer. Matematikailag egyenlőség formájában kifejezve [1]: ahol qj a mechanikai rendszereket leíró általánosított koordináták, i = 1 ... k ... Wikipedia