Kirchhoff első törvénye
Az elektromos áramkör egyedi vezetékei egymással párhuzamosan és vegyesen sorolhatók egymáshoz. Ebben az esetben a vezetékek soros és párhuzamos kapcsolata a vegyületek fő típusai, és a vegyes vegyület az összesített.
A vezetékek sorozatos bekötése
Egy sor vezetékeinek összekapcsolása olyan vegyületet értünk, amikor a végén az első vezeték van csatlakoztatva az elején a második vége a második vezeték van csatlakoztatva az elején a harmadik, és így tovább (1. ábra).
A több soros csatlakozóból álló áramkör teljes ellenállása megegyezik az egyes vezetékek ellenállásának összegével:
A soros áramkör egyes részeiben lévő áram mindenütt azonos:
Example1. A 2. ábra három soros csatlakozású r1 = 2 Ω, r2 = 3 Ω, r3 = 5 Ω ellenállást tartalmazó áramkör. Meg kell határozni a V1 feszültségmérő értékeket. V2. V3 és V4. ha az áramkör az áramkörben 4 A.
Az egész lánc ellenállása
Az Ohm törvénye szerint az áramkör termináljain a feszültség megegyezik az áramkör áramával, megszorozva az ellenállással:
Ennek következtében a V. feszültségmérő a feszültségforrás csatlakozóihoz kapcsolódik 40 V feszültséget jelez.
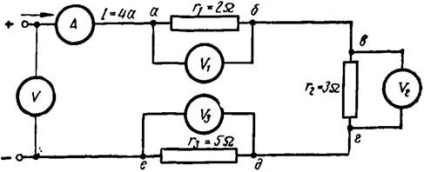
2. ábra. Az elektromos áramkör egyes szakaszaira vonatkozó feszültségmérési séma
Voltmérő V1. az a és b pont között. 8 V.
Az ellenállás r2-ben van egy feszültségcsökkenés:
Voltmérő V2. a c és d pontok közé sorolva 12 V jelenik meg.
Feszültségcsökkenés az ellenállásban r3:
Voltméter V3. amely a d és e pont között szerepel, 20 V értéket mutat.
Ha a voltmérő az egyik végén az a pontig csatlakozik. a másik végét pedig a pont is megmutatja a potenciális különbség ezen pontok között az összegével egyenlő a feszültség esik az R1 és R2 ellenállások (8 + 12 = 20).
Így V. voltmérő feszültség mérésével a kapcsai és a kapcsolódó pontok közötti egy és e. Itt a potenciális különbség ezek között a pontok, vagy az összeget a feszültség az ellenállások r1. r2 és r3.
Ezért látható, hogy az elektromos áramkör egyes részeiben fellépő feszültség összege megegyezik az áramkör terminálján lévõ feszültséggel.
Mivel egy soros kapcsolatban az áramkör áramlása minden szakaszban megegyezik, a feszültségcsökkenés arányos a szakasz ellenállásával.
2. példa. A 10, 15 és 20 Ohm három ellenállását sorba kapcsoljuk, amint az a 3. ábrán látható. Az 5A-áramerősség meghatározza a feszültségcsökkenést minden egyes ellenálláson.
3. ábra. Például 2
Az áramkör teljes feszültsége megegyezik az áramkör egyes szakaszainak feszültségcsökkenéseinek összegével:
Párhuzamos vezetékek csatlakoztatása
Párhuzamos kapcsolat a vezetékek olyan vegyületet értünk, amikor az elején az összes vezeték csatlakozik egy ponton, és a végén a vezetékek -, hogy egy másik pont (4. ábra). Az áramkör kezdete a feszültségforrás egy pólusához csatlakozik, és az áramkör vége a másik oszlophoz.
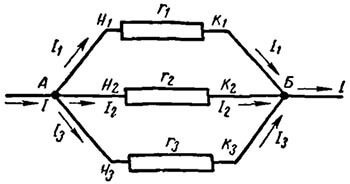
4. ábra: A vezetékek párhuzamos csatlakoztatására szolgáló áramkör
Az ábrán látható, hogy a vezetékek párhuzamos bekötése az áram áthaladásához több úton van. Az A. elágazási pontra áramló áram tovább terjed a három ellenállás mentén, és egyenlő az e pontból folyó áramok összegével:
Ha az ágpontba érkező áramok pozitívnak tekinthetők, és a kimenő negatívok, akkor az ágpontra írhatunk:
vagyis a lánc minden csomópontjára mutató áramok algebrai összege mindig nulla. Ez a kapcsolat, amely összeköti az áramlatokat a lánc elágazása bármely pontján, Kirchhoff első törvényének nevezzük. Meghatározunk egy első Kirchhoff-törvény, és megszólal egy másik készítményt, azaz az összeg a folyó áramok az áramkörben szerelvény az összege folyó áramok a csomópontot.
Általában az áramkörök kiszámításakor az áramlások iránya az ágakhoz kapcsolódó ágakban ismeretlen. Ezért ahhoz, hogy képes legyen a legelső törvénye Kirchhoff egyenlet bejegyzések szüksége megkezdése előtt áramkör tervezése önkényesen dönt, az úgynevezett pozitív irányba az áramok minden ágában és megjelöli az nyilak az ábrán.
Az Ohm törvényének alkalmazása. a fogyasztók párhuzamos kapcsolatának teljes ellenállásának kiszámítására szolgáló képletet lehet kiszámítani.
Az A. pontra érkező teljes áram egyenlő:
Az egyes ágak áramai a következő értékekkel rendelkeznek:
Kirchhoff első törvényének képletével
A zárójel egyenletének jobb oldalán a következőket kapjuk:
Az egyenlet mindkét oldalát U-rel csökkentve kapjuk meg a teljes vezetőképesség kiszámításának képletét:
Így párhuzamos kapcsolattal a rezisztencia helyett az ellenállás nő, de a vezetőképesség.
3. példa Határozza meg a három párhuzamosan kapcsolt ellenállások teljes ellenállását, ha r1 = 2 Ω, r2 = 3 Ω, r3 = 4 Ω.
4. példa A hálózatra párhuzamosan öt, 20, 30, 15, 40 és 60 ohm ellenállást csatlakoztatunk. Határozza meg a teljes ellenállást:
Meg kell jegyezni, hogy az összes elágazó ellenállás kiszámításánál mindig kevesebb, mint a legalsó ellenállás az ágon belül.
Ha a párhuzamos ellenállások egyenlőek egymással, akkor az áramkör teljes ellenállása r egyenlő az egyik r1 ág ellenállásával. osztva az ágak számával n:
5. példa. Határozzuk meg a négy egymással párhuzamosan kötött 20 Ohm-os ellenállások teljes ellenállását:
A vizsgálathoz próbáljuk megkeresni az elágazó ellenállást a képlet szerint:
Mint látható, a válasz ugyanaz.
6. példa. Meg kell határozni az egyes ágak áramát az 5. ábrán bemutatott párhuzamos kapcsolattal, a.
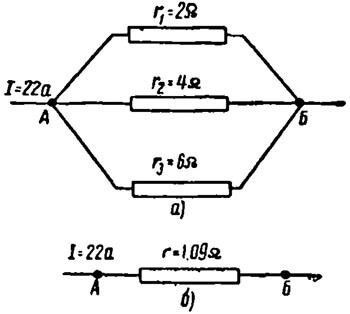
5. ábra. Például 6
Lássuk a lánc teljes ellenállását:
Most egyszerűen ábrázoljuk az összes ágat, mint egy ellenállást (5. ábra, b).
Az A és B pont közötti feszültségcsökkenés a következő lesz:
Visszatérve az 5. ábrára, látjuk, hogy mindhárom ellenállás 24 V lesz, mivel az A és B pontok között van.
Figyelembe véve, hogy az első ág elágazik az ellenállás r1-gyel. látjuk, hogy ebben a szakaszban a feszültség 24 V, a szakasz ellenállása 2 Ohm. Az Ohm-törvénynek az áramkörszakaszra vonatkozó szakasza szerint a jelenlegi szakasz ebben a szakaszban lesz:
A második ág áramlása
A harmadik ág jelenlegi
Ellenőrizzük Kirchhoff első törvényének megfelelően
Ennek következtében a probléma helyesen megoldódott.
Figyeljünk arra, hogy az áramok hogyan oszlanak el a párhuzamos kapcsolatunk ágai között.
Amint láthatjuk, az első ág ellenállása a második ág ellenállásának fele, és az első ág áramlása kétszerese a második ág áramának. A harmadik ág ellenállása az első ág ellenállásának háromszorosa, és a harmadik ág áramlása háromszor kisebb az első ág áramerősségénél. Így azt a következtetést lehet levonni, hogy a párhuzamos kapcsolású ágakban az áramok fordítottan arányosak ezeknek az ágaknak az ellenállásával. Így a nagyobb ellenállású ág kisebb áramerősségű áramot fog áramolni, mint egy ágat.
Két párhuzamos ágra természetesen használhatjuk a fenti képletet is.
Azonban a vezető párhuzamosan történő teljes ellenállását ebben az esetben könnyebb kiszámítani a következő képlet segítségével:
Vegyes vezeték csatlakozás
A vezetékek vegyes összekötése egy olyan kapcsolat, ahol az egyes vezetékek sorozata és párhuzamos kapcsolata is van. Egy példa a 6. ábrán látható kapcsolat.
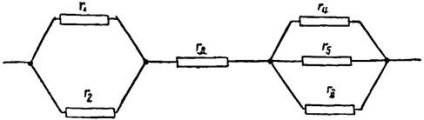
6. ábra A vezetékek vegyes csatlakozásának ábrája
7. példa Határozzuk meg a 6. ábrán látható kevert vegyület teljes ellenállását, ha
Keresse meg az első ág teljes ellenállását:
A második ág teljes ellenállása:
Az áramkör teljes ellenállása:
Forrás: Kuznetsov MI "Villamosmérnöki alapismeretek" - 9. kiadás, felülvizsgált - Moszkva: Felsőoktatás, 1964 - 560p.