Polyhedra alapfogalmak
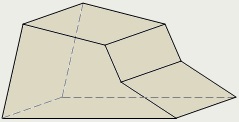
Néhány háromdimenziós forma, vizsgálták szilárd geometriát, az úgynevezett szervek vagy geometriai testek. Vizuálisan szervezetet kell elképzelni, mint része a tér által elfoglalt fizikai testet, és korlátozott felületet.
Polyhedron úgynevezett geometriai test, amelynek a felületi áll véges számú sík sokszög.
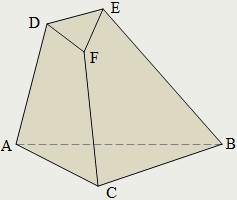
Konvex poliéder nevezzük, ha található egyik oldalán egy síkot bármilyen sokszög felületet alkotó a poliéder.
A sokszögek alkotó poliéder felületi, úgynevezett annak arcok; oldalán sokszögek - bordák; felsők - poliéder:
ABC. DEF. Abed. BCFE. ACFD - határán;
AB. BC. AC. DE. EF. DF. AD. BE. CF - bordák;
A. B. C. D. E. F - ABCDEF csúcsai a poliéder.
Euler-tétel poliéder.
Ha V - a csúcsok száma a konvex poliéder, R - a szám a bordáját, és G - arcok száma, a valódi egyenlőség:
V - R + G = 2.
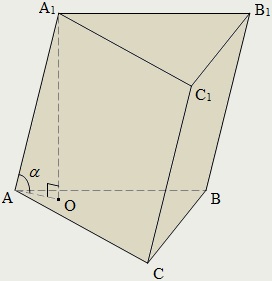
Prism nevezzük poliéder, amely két sík sokszög amelyek fekszenek különböző síkokban és párhuzamosan állnak fordítást, és az összes összekötő szakaszok megfelelő pontjai ezen sokszögek. Sokszögek, amelyek vitatták, úgynevezett bázisok a prizma, és a szegmensek, amelyek összekötik a megfelelő csúcsok - az oldalsó szélei a prizma.
A bázisok a prizma egyenlő és feküdjön párhuzamos síkokban.
Az oldalsó prizma élei egyenlő és párhuzamos.
A felület a prizma két bázisok és oldalsó felületek.
Az oldalsó felület egyes prizma áll paralelogramma, amelyek mindegyike a két oldalán a megfelelő bázis oldalán és a másik két - a szomszédos oldalsó széleit.
A magassága a prizma bármelyike merőlegeseket lefolytatott egyik helyről a másik bázis prizma alapsík.
Prism nevezzük n -ugolnoy, ha az alap - n-gon.
Mintegy A1 - a magassága a prizma;
α - hajlásszöge az oldalsó széleken, hogy a bázis a prizma.
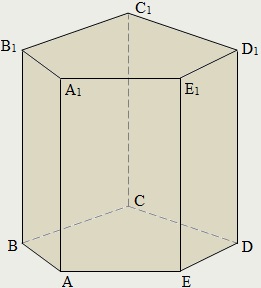
Prism hívják közvetlen, ha a bordák merőlegesek a síkok a bázisok. Egyébként ez az úgynevezett ferde hasáb.
Az oldalsó felületei egyenes hasáb - téglalapok.
Az oldalsó szélén egy egyenes hasáb van a magassága.
Az oldalsó felülete egyenes hasáb egyenlő a termék a az alap kerületét a magassága a prizma:
Prism nevezzük szabályos, ha bázisok szabályos sokszög.
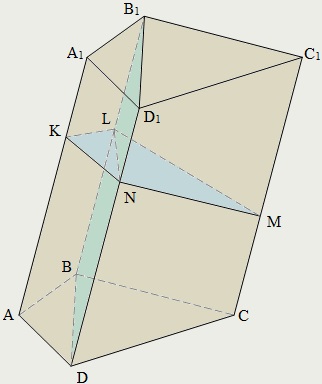
Prism keresztmetszeti párhuzamos síkokban a oldalélek paralelogramma. Különösen a paralelogramma egy átlós keresztmetszete. Ez a szakasz a síkok segítségével a két oldala, nem tartoznak ugyanaz az arc:
BB1 D1 D - átlós részének.
Ha egy tetszőleges ferde prizma tartásba szakasz merőleges az oldalsó széleit áthaladó összes oldalélei és ez a rész kijelölt terület S⊥. és a kerület - R⊥. akkor:
- A jobb oldali felületét prizma:
- A kötet a prizma igaz:
A prizma:
Mindenesetre prizma teljes felület tekinthető a négyzetösszege oldalsó felülete és a duplájára alapterülete:
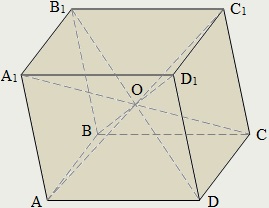
A prizma, amelynek alapja egy paralelogramma nevezzük téglatest.
Minden részletét a doboz - paralelogramma.
Face a doboz, nincs közös csúcsok nevezzük szemben.
A szemközti felületek párhuzamosak és egyenlő.
Átlós a doboz, mint a poliéder általában az úgynevezett összekötő szakasz a tetején a doboz, nem hazudnak, annak egyik arca.
téglatest átlói metszik egy ponton, és a metszéspont kettéváló.
Metszéspontja az átlók a doboz közepén szimmetria.
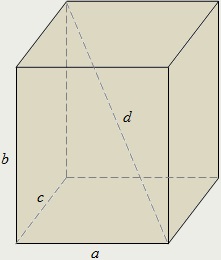
Derékszögű paralelepipedon úgynevezett egyenes parallelepipedon, a bázis, amely abban rejlik egy téglalap.
Minden arc egy téglatest téglalapok.
Élek hossza a derékszögű paralelepipedon, amelyik egy vertex, úgynevezett annak mérések vagy lineáris méretei.
A téglatest három dimenzióban.
A derékszögű paralelepipedon négyzet bármely átlós egyenlő a négyzetének összege a három méretei:
A hasáb alakú igaz:
- A teljes felület:
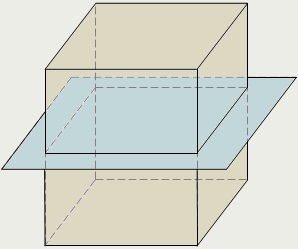
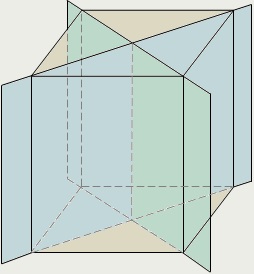
A hasáb alakú, mint minden téglalap, központjában szimmetria - a metszéspontja az átlók. Ő is három szimmetriasíkjaiban középpontján áthaladó szimmetria párhuzamos, egymással szemben lévő arcokat. Az első ábra a fent megadott, azt mutatja, az egyik ilyen síkok. Ez végigfut a közepén a négy párhuzamos széle a doboz.
Ha a doboz minden lineáris méretei különbözőek, ő nem más szimmetriasíkjaiban, de ezek közül három.
Ha a box két lineáris méret egyenlő, vagyis ez is igaz négyszögletes hasáb, akkor is két szimmetriasíkjaiban. Ez átlós síkban keresztmetszet látható a második szám.
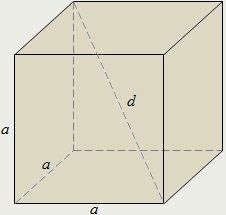
Téglatest amelyben mind a három dimenziója egyenlő hívják kocka.
kocka átlós négyzetgyök háromszor oldalán:
- A teljes felület:
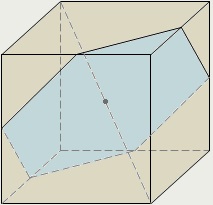
Négy kocka szakaszok szabályos hatszög (egyikük látható) - ezeket a szakaszokat át a központ a kocka merőleges négy átló.
Egy kocka kilenc szimmetriasíkjaiban:
- három közülük áthaladó közepén a négy párhuzamos élei a kocka, mivel a szakaszok a négyzetek;
- A többi hat - valamennyi szakasz a sík átlója a kocka.
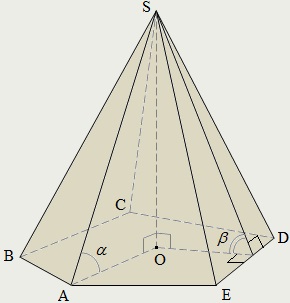
A piramis (például SABCDE) nevezzük poliéder, amely egy sík sokszög (ötszög ABCDE) - alapja a piramis pont (S), nem fekvő bázis síkban, - a piramis vertex és minden szegmens összekötő csúcsa a piramis a bázis pont.
Szegmensek (SA. SB. SC. SD. SE), amely összeköti a tetején a piramis a bázis csúcsok nevezzük oldalsó élei.
A felület a piramis áll egy bázis (ötszög ABCDE) és az oldalsó arcok. Minden oldalon arc - egy háromszög. Egyik csúcsok a csúcs a piramis, és a másik oldala - oldalán az alap a piramis:
δSAB. δSBC. δSCD. δSDE. δSEA - élek.
Side felülete a piramis a négyzetösszege oldalsó felületein.
A magassága a piramis (SO) merőleges által végzett csúcsa a piramis alapsíkkal.
Piramis úgynevezett n -ugolnoy ha annak bázis N-gon. A háromszög alakú piramis is nevezik a tetraéder.
α - szög SA oldalsó szélei a piramis, hogy az alap síkjában;
β - a dőlésszög az oldalsó felület (SED) a piramis, hogy az alap síkjára.
Az alap magassága a piramis közepén a köré rajzolt kör a alapja a piramis, akkor és csak akkor, ha az egyik feltétel:
- minden oldalsó szélei egyenlő;
- oldalirányú bordák a alapsíkon egyenlő szögek;
- oldalirányú bordák azonos szöget zárnak be a magassága a piramis.
Az alap magassága a piramis közepén beírható kör az alapja a piramis, akkor és csak akkor, ha az egyik feltétel:
- az oldalfelületek vannak döntve, hogy a bázis síkot ugyanolyan szögben;
- a magassága a oldalfelületek egyenlő;
- oldalfelületek azonos szöget zárnak be a magassága a piramis.
A kötet a piramis harmadik munkaterület, a bázis a magassága a piramis:
V = 1/3 · Sosn h.
A teljes felülete semmilyen piramis összegével egyenlő az oldalirányú felszíne és a okok:
Piramis síkokban áthaladó csúcsa, háromszögek. Különösen, a háromszög átlós keresztmetszete. Ez a metszeti sík áthaladó két nem szomszédos szélei oldalán a piramis.
Hosszú I tervezett és végre! Olyasmi, mint ez a történet a mi csoport VKontakte. Kétségei vannak a szükségességét annak létezését dobni, és az első anyag közösség lefektetett.
Ez kiterjeszti a funkcionalitást a főmenübe.