A skaláris szorzata két vektor
Belső szorzata vektorok és egy szám egyenlő a termék a oldalainak hossza a koszinusza a köztük lévő szög.
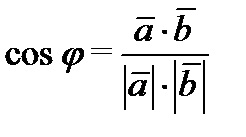
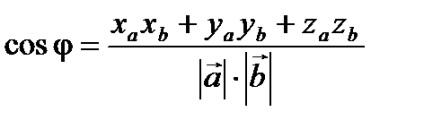
Ha a vektorok meghatározott koordináta formájában. .
akkor a skalár terméket a következőképpen számítjuk ki:
A tulajdonságok a skalár termék:
Vector termék. Tulajdonságok. Alkalmazás.
A vektor terméket vektorok nevezzük vektor. kielégíti az alábbi feltételeket:
1). ahol j - és az a szög között vektorok.
2) egy vektor merőleges a vektorok és a
3). és a forma egy jobbkezes vektorok.
Tulajdonságok a vektor termék a vektorok
5) Ha a megadott vektorokat a derékszögű koordinátarendszerben az egység vektorok. az
-vektorok koordinátatengelyeken Ox, Oy, Oz, illetve:
6) A geometriai jelentése a vektor termék a vektorok az a terület a paralelogramma által alkotott vektorok és. .
Megjegyzés: ha a kivonni kívánt terület egy paralelogramma, akkor meg kell vizsgálni az első,
A vegyes termék vektorok. Tulajdonságok. Alkalmazás.
Vegyes termék három vektor
A kevert termék a következő tulajdonságokkal rendelkezik:
1). ha mind a három vektorok párhuzamosak ugyanezen síkkal (legyen egy síkban);
2) egy ciklikus permutáció
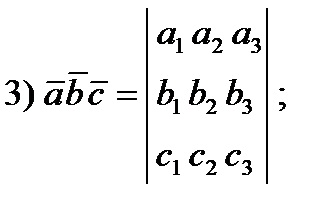
4) a kötet egy paralelepipedon, és kialakult a vektorok. jelentése
ha a * b * c> 0, akkor a hármas a, b, c - jobb, ha a * b * c<0, то тройка a,b,c - левая
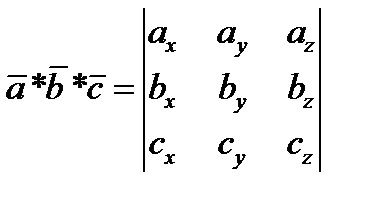
Az a feltétel, coplanarity 3 vektorok.
Vector alapon. vektor koordinátái. Bővítése a vektor alapján.
Bázis - egy csoport-a c / o, amely kifejezi az összes ling helyet. A 3hmernom vehető ve alapján áll egy 3-nekomplan nyhv-in. A pl látnia 2-ra.
Ortogonális bázisa álló vzaimnoperpendik-nyhv-ben. ()
Normalizált alapon áll egy kor-árok ().
Alapértelmezett hogy ortogonális bázisa.
Expansion alapján:
-előrejelzések vagy Coord in-ra.
13.Usloviya kollinearitást, ortogonalitás, coplanarity vektorok.
A feltétel ortogonalitását vektorok
Két ortogonális vektorok feltéve eltűnő a skalár szorzat:
Állapota kollinearitása vektorok
Ha a vektorok egy egyenesen vannak (hazugság egyenes vagy közvetlen naparallelnyh), azaz a köztük lévő szög értéke 0 vagy 0 180, a kereszt termék nulla:
A feltétel coplanarity vektorok
A vektorok egy síkban (ugyanabban a síkban), ha a bekevert termék nulla:
Lineáris operátorok. A sajátértékek és sajátvektorok lineáris operátor. Lineáris csere modell.
P a mező fölé, van egy lineáris operátor, ha
1) minden vektorok
2) bármely vektor és bármely.
Sajátvektorok és sajátértékek a lineáris operátor.
1) A mátrix egy lineáris operátor:
enged # 966; -L.O. vektor terek a mező fölé V P, és az egyik a bázisok V:
enged
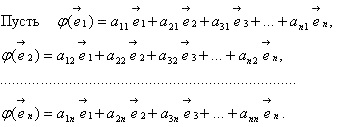
Ezután a mátrixot LO # 966;:
2) közötti kapcsolat a mátrix egy lineáris szereplő különböző bázisok:
M (# 966) - mátrix LO # 966; a régi alapon.
M1 (# 966) - mátrix LO # 966; Az új alapokra helyezése.
T - mátrixa az átmenet az idősebb, hogy az új bázis alapján.
2) Műveletek lineáris operátorok:
enged # 966; és f - a különböző LO vektortér V.
majd # 966; + F - az összeg a lineáris operátorok # 966; például F.
k · # 966; - szorzás LO skalár k.
# 966; · f - a termék lineáris operátorok # 966; például F.
Yavlyayuisya is LO vektoronogo tér V.
4) A kernel a lineáris operátor:
d (# 966) - mag dimenziója LO # 966; (Defect).
5) A kép egy lineáris operátor:
futott # 966; - Rank LO # 966; (Dimension Jm # 966;).
6) sobsvenno vektorok és sajátértékei a lineáris vektor:
# 61623; enged # 966; - LO vektor terek a mező fölé V és a P, és
Ha az # 955; - sajátérték
- sajátvektor LO # 966;, töltés # 955;.
# 61623; A karakterisztikus egyenlet LO # 966;:
# 61623; A sajátvektorai megfelelő sajátértékek # 955;:
# 61623; LO vektoronogo tér nevű LO egyszerű spektrum, ha # 966; ha # 966; Ez pontosan n sajátértékek.
# 61623; ha # 966; - LO egyszerű spektrum, van egy alapja sajátvektorok, amelyek tekintetében a mátrix LO # 966; átlós.