transzverzalitási
A gyakorlatban problémák vannak a meghatározó funkcionális extrémuma amikor a végén a változatos görbék vannak rögzítve, ingyen, vagy tartoznak bizonyos fajta. Ezek határpontokhoz kell végezni az úgynevezett transzverzalitási körülmények között.
transzverzalitási feltételei rögzített intervallum T:
ki kell vizsgálni együtt a határ értékeket x (t), amely lehet rögzített vagy szabad (ábra. 1).
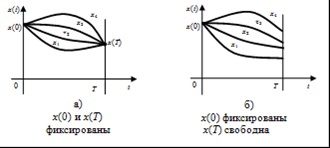
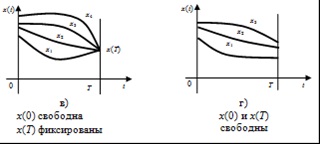
Ábra. 1.2.1 Lehetséges funkciók X (t) függően peremfeltételek
Ha egy határ érték x (TGR) be van állítva (ahol TGR = 0 vagy T), akkor variációs nullának kell lennie, és az értékét a derivált nincs korlátozás.
Ha egy határ érték x (TGR) mentes, akkor a variáció lehet véletlenszerű, ezért kell nulla [2].
Tekintsük a különböző feladatokat, hogy optimalizálja a rögzített intervallum T.
1. Kezdeti X (0), és a végén az X (t) értékek a kimeneti változó megadott (probléma fix határpontokhoz, ábra. 1.2.1 a).
Ebben a feladatban az összes lehetséges görbe x (t), amely kérik között az extremális x * (t), meg kell kezdeni, és a végén a fix pont. Variációk (0) és (T) nullával egyenlő, és az értéke a származtatott hiba intézkedések határain intervallum nincs korlátozás. Az integrációs állandók C1, C2 nyert peremfeltételek x (0), X (t), és a transzverzalitási feltétel nem használják.
2. Kiindulási x (0) a kimeneti változó értéke rögzített és véges x (T) - álló (a probléma, hogy a jobb határ, ábra .12.1, b).
Mivel x (T) lehet feltételezni, tetszőleges értéket, a variációs (T) lehet bármely így transzverzalitási feltétel teljesül csak nulla-származék
Így a két peremfeltételek x (0), és lehetővé teszi, hogy megtalálják az értékek a integrációs állandók C1, C2.
a peremfeltételek a problémát mozgatható kiindulási pont x (0), és a rögzített vég x (T) (a probléma hogy a bal oldali határ ábra. 1.2.1 a) hasonlóan definiáljuk.
A bal szélén variáció (0) lehet bármikor. Ez a feltétel, és határérték x (T) konstansok az integráció.
4. Kiindulási x (0), és a végén az X (t) kimeneti értéke rendelkezésre álló mennyiség (a probléma a laza határpontokhoz, ábra. 12,1 g).
Mivel a variáció (0) és (T) bármelyike lehet a transzverzalitás feltételek, ebből következik, hogy a határokat kell tűnnie származékot hiba intézkedések
Ezért a folyamatos integráció által meghatározott C1 és C2.
Tegyük fel, hogy adottak a következő funkcionális
ahol: funkció jellemzi a rendszer állapotát időpontban t = T.