Oia transzverzalitási
Az általános esetben adható egy sor kezdeti állapotok, és több end rendszerek
Meg kell találni az ellenőrzés. átalakítja a rendszert a mező területén bányákban. időben.
Ebben az esetben, az optimalizálási folyamat akkor szükséges, hogy legyen egy folytonos vektor függvény kielégíti nem csak a maximális állapotban, de iusloviyam transzverzalitási mindkét végén a pálya (t).
transzverzalitási feltétel, hogy a vektor merőleges érintő sík terület és az elején és a végén az út. Feltételezzük, hogy a funkciók ogranicheniyinepreryvny és folytonosan differenciálható himlő. Tegyük fel továbbá, hogy a régió és a korlátozott, zárt és konvex.
Nézzük meg, mi feltételeket kell kielégíteni a funkció (t), ha a kiindulási pont tartozik a régió kezdeti állapotok és végpontja az eredete.
mert - zárt halmaz, a lényeg a határpont a készlet: ha ő nem volt egyedül, hogy ez időbe telik el, hogy lépjen túl a határt a készlet, és nem lenne optimális.
Hagyja, - a kiindulási pont az optimális eljárás. mozgás ideje ettől a ponttól a végéig. Készítünk egy domain elérhető államok megfelelő vremeniT.
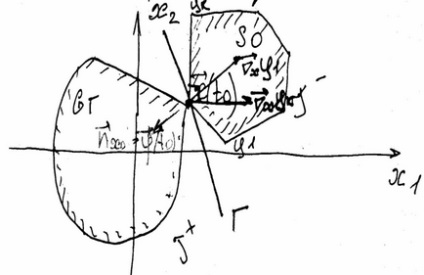
így kiderül, hogy a kiindulási pont egy határ pont a két: több eredeti és több elérhető állapotok vremyaT.
A Hahn-Banach, két diszjunkt konvex és lehetnek elválasztva egy hipersík. Ha ezek a régiók van egy közös pont, ez hipers'ıkot utalás területeken ezen a ponton.
Döntetlen hipersíkot H. Ha a hipers'ık G tekinthető utalás területén hozzáférhető államok, az normális, hogy a hipers'ık egy vektor.
Találunk közötti kapcsolat normális, hogy a korlátozások: A merőlegesek irányul vnutrS0. mert
Azok számára, korlátok, amelyek nem hatékonyak a Kuhn-Tucker tétel ,. Aztán kapunk
Ha a mozgás alól indul és ér véget a területen, a feltétel lesz, mint ez:
A kombináció a két feltétel az úgynevezett transzverzalitási feltételekkel.
Megjegyzés: ha a régió az utolsó pont tovybiraetsya önkényesen. Amennyiben a célterület - minden fázisban térben, akkor = 0, mivel minden koeffitsientybudut nulla (és minden korlátozás, illetve hatástalan).
8.Printsip maximális helyhez rendszerfelügyeleti feladatok az integrált minőségi kritérium.
ellenőrzési problémát beépített minőségi kritériumoknak:
FunktsiyaLnepreryvna annak érvek és folyamatos részleges származékok .. Ha a függvény L = 1, az optimális problémát.
Az az állapot, a maximális elvi álló rendszer:
irányítani probléma beépített minőségi kritérium, ha a funkcionális célja terület és a állapotegyenlet nem függ explicit időben.
Hagyja, hogy az állam egy dinamikus rendszer által leírt nemlineáris differenciál. egyenlet formájában :.
Adott régióban. az eredeti állapot S0 és konechnogoSf. Ez szükséges, hogy meghatározzák a feltételeket, a macska. Kielégítő. Optimális az irányítást a tolerancia és a pálya megfelelő optimális kezelését, kielégíti a peremfeltételeket.
.
Úgy gondoljuk, hogy a végén idő beállítása tne.
Tegyük fel, hogy L nem kifejezetten az időtől függenek, és a pozitív.
Mozog egy valós idejű tc néhány fiktív vremeni .. Ezt szem előtt tartva, az eredeti rendszer dif.ur. Tart a formában:. (). Ezután a funkcionális otnositelnoprinimaet formában: (*) - csökken az optimális teljesítményt.
Transzfer a feltételeket az optimális teljesítményt a feladatok széles osztálya problémákat. Legyen () eljárás optimális smysleminformuly (*), akkor megfelel a maximális elv az optimális problémát.
Van egy funkció tartozás. macska. Vol. feltételek: ;; ahol
A feltétel a legnagyobb:
Valamint az optimális pályája a Hamilton-függvény a következő formában:
Transzverzalitási állapotban.
Tekintsük az szerkezet helyettesítő expr-e az F-II Hamilton (1)
(2) Ezt a funkciót nevezik. Hamilton rendszer szerves minőségi kritérium. Hamilton = 0 csak mentén optimális trajektória. Általában, ha van egy az idő függvényében: (3).
Bevezetés Hamilton lehetővé teszi számunkra, hogy általánossá maximális állapot, azaz a azt mondhatjuk, hogy ha () -opt. folyamat, a következő feltételeknek kell teljesülniük:
Ott kell lennie egy funkciót a macskát. Az alábbiak közül melyik igaz. képarány Ia-a); b)
A feltétel a legnagyobb:
Hamilton mentén az optimális útvonalat = 0.
Transzverzalitási állapotban.
Mi jár a hagyományos idő k valós vremenit:
,- feltétel 1a végezzük.
Nézzük (1b), mozgassa otkt: - feltétel 1b végezzük.
Ellenőrizze vez. 2: ezért ,,
Vez. 3: A Hamilton mentén nagykereskedelem. path = 0, akkor következik annak megkötésére, és alapul usl.2
Vez. 4: Mivel transzverzalitási feltétel bármely f-CIÓ bármely Hamilton Hamilton nem tartalmazza, azok teljesen megmarad. megjelenésük:
Megjegyzés1: Kaptunk egy állapot maxv feltételezés, de ők végzik az általános esetben.
Megjegyzés2: ConstP0 általában úgy gondolták, = -1. P0 = -1