logaritmikus differenciálás

Kiszámításakor az származéka logaritmusát a termék, hányadost vagy gyökér szinten, hogy egyszerűsítse a származékkal végzett előzetes átalakulás (lásd. 10. példa (u)).

Bizonyos esetekben célszerű, hogy megtalálják a származék egy adott funkciót, először a logaritmus (alapértelmezett értünk természetes logaritmusa). Ezután keresse meg a származék a logaritmus e, és megtalálja azt a származékot adott funkció. Ez az úgynevezett logaritmikus differenciálás.

logaritmikus differenciálás módszer megkönnyíti, hogy megtalálja a származék jelentős teljesítmény-típusú függvény

,

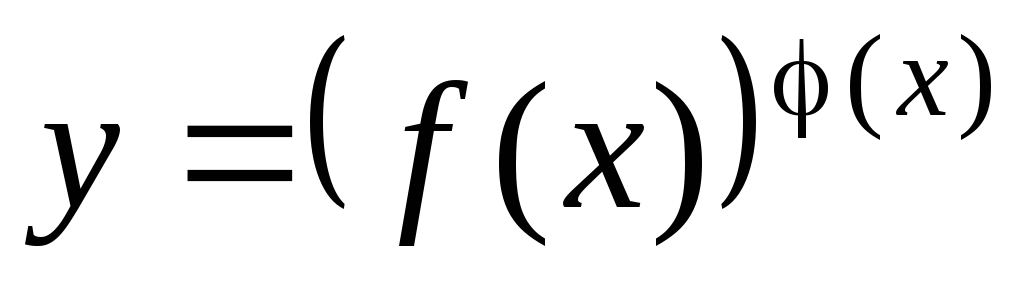
ahol

és - differenciálható függvény argumentum .

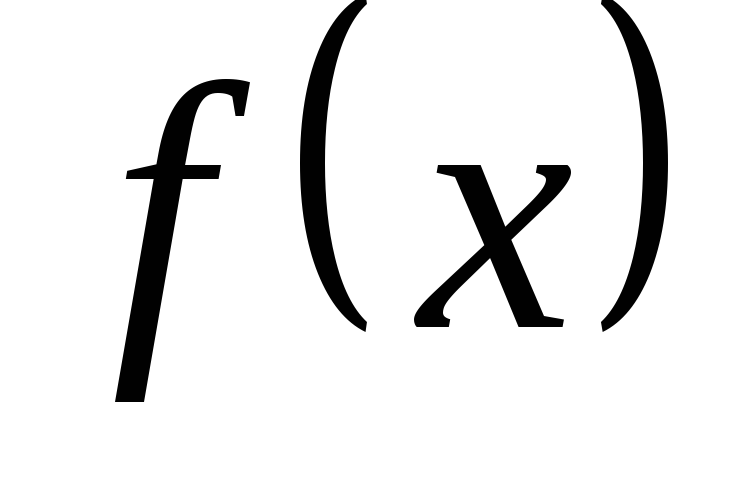
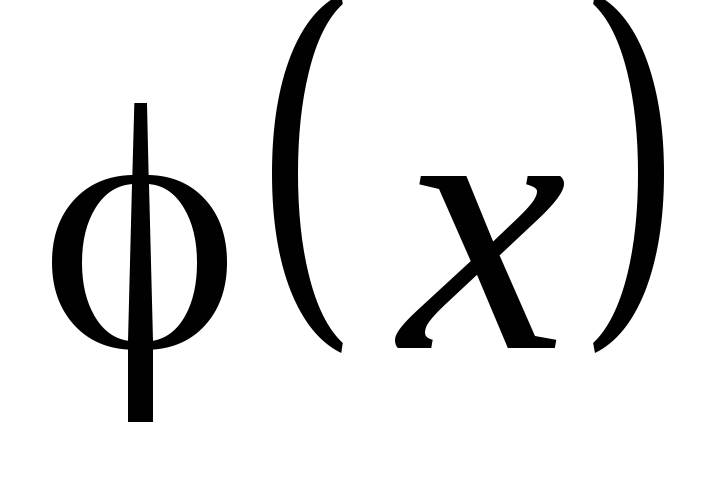
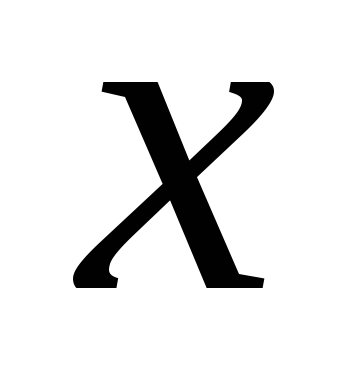
Keresse meg a származék

.

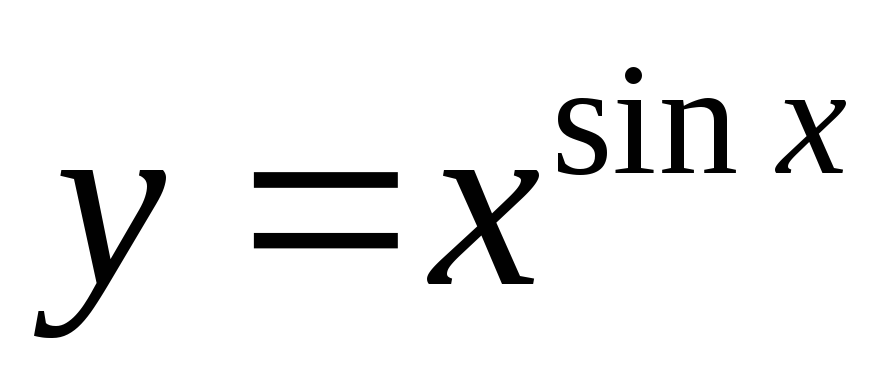
Logaritmusát mindkét oldalán a funkciókat, és átalakítja a kifejezést:

.

Most különbséget egyenlet implicit meghatározott funkció:

;

;

;

;

mert

, végül megkapjuk:

.

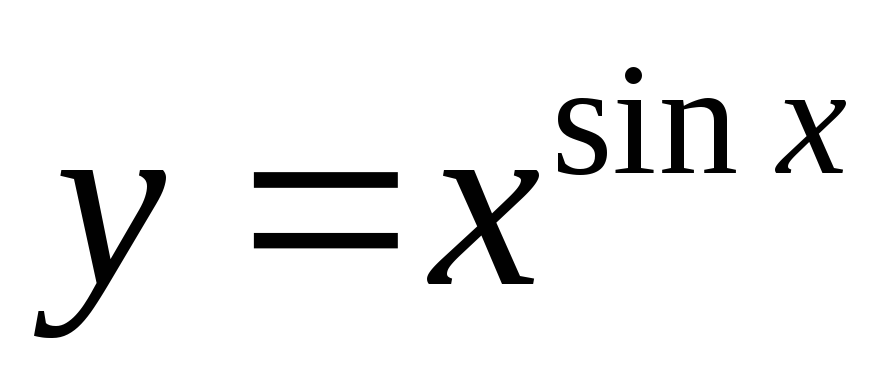
Származékai magasabb rendű

Származék érdekében 2 funkció

a származék az első deriváltját, azaz

.

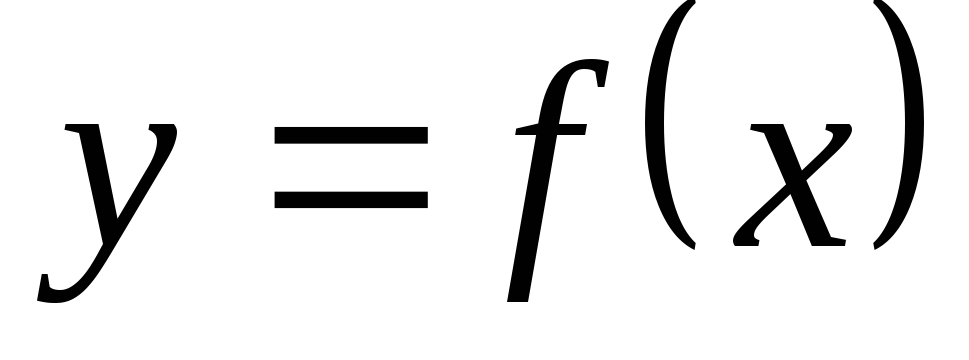
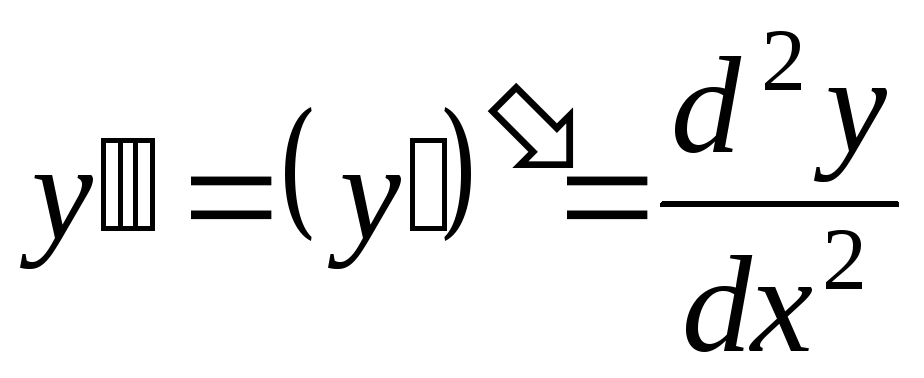
Hasonlóképpen, a származékot a 3. sorrendben a funkció

a származéka második deriváltja, azaz,

.

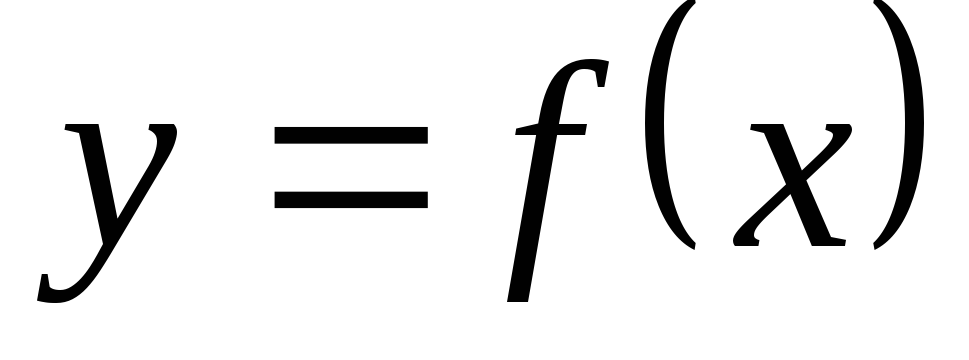
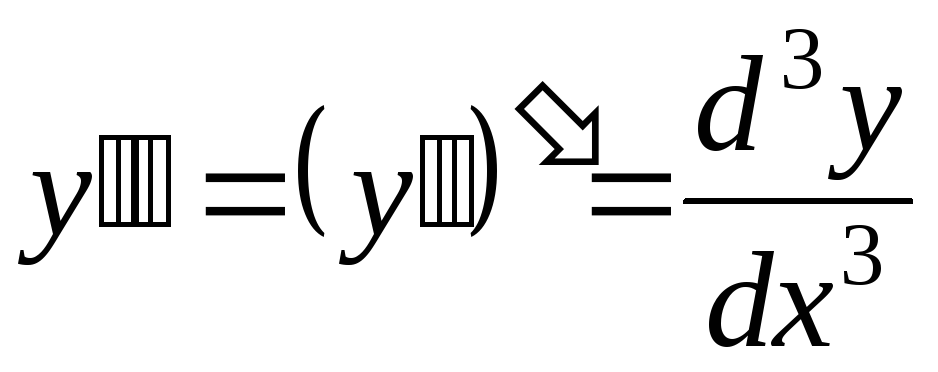
Így, a származék

-Az első, hogy a függvény Ez a származék a-származék -kell lennie, vagyis,

.

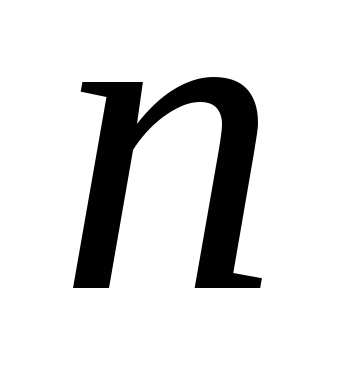
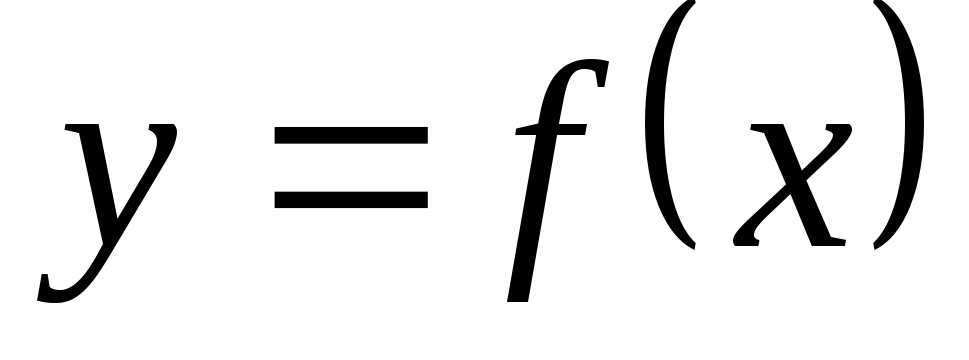
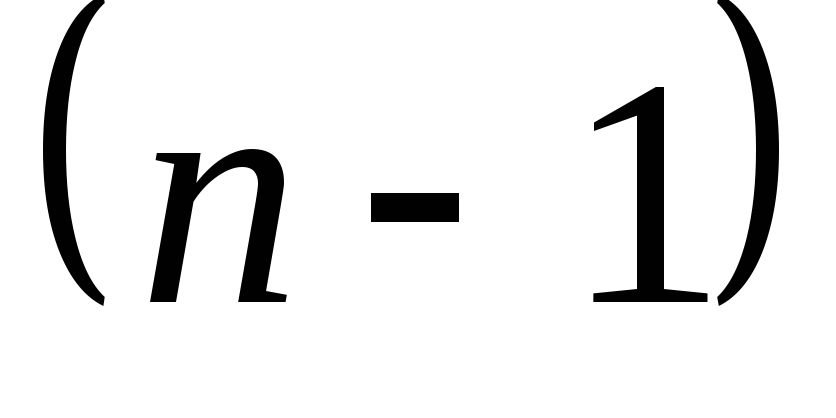
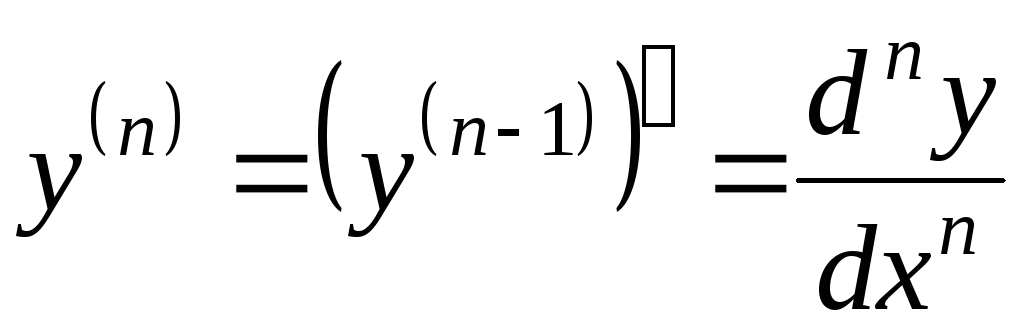
Következésképpen, a származékos

-edrendű származék kell szekvenciális keresés az első, majd a második, majd a harmadik, stb hogy-érdekében.

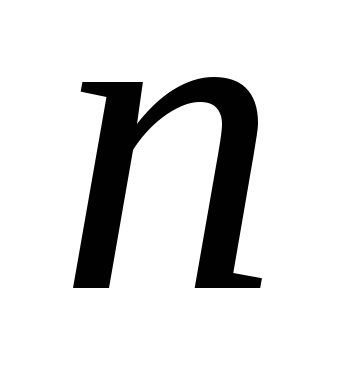
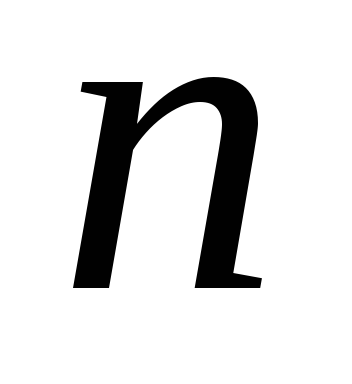
Keresse meg a harmadik származék

funkciók .

;

;

.

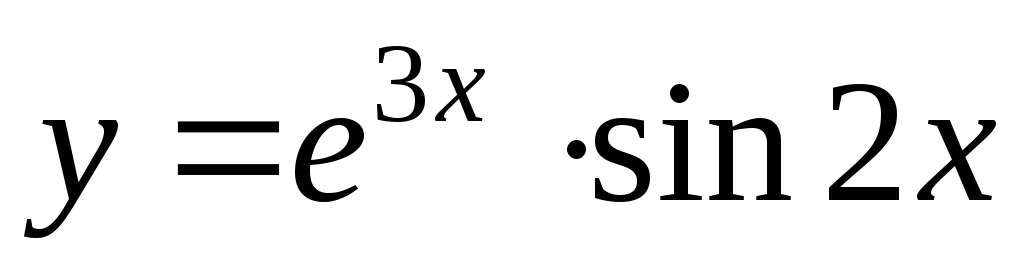
2.3. eltérés jellemzői

A meghatározása a származtatott tulajdonságok és a korlátok, ha

ahol

- végtelenül ().

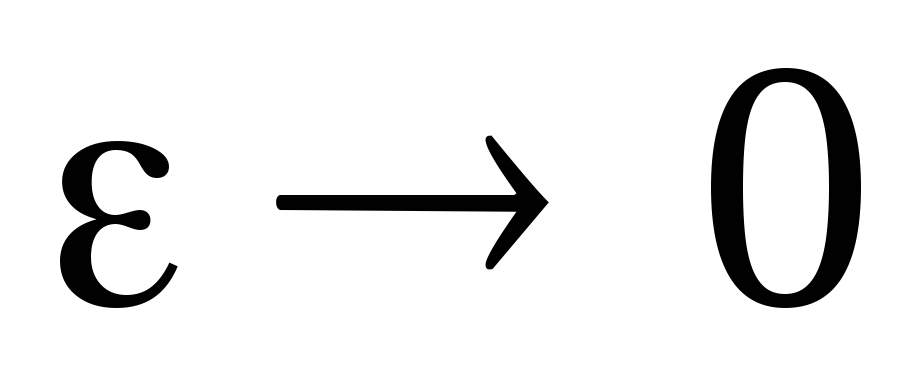
expressz

és megkapjuk, hogy:. mert, majd a jövőben lehet figyelmen kívül hagyni, és ezt kapjuk:

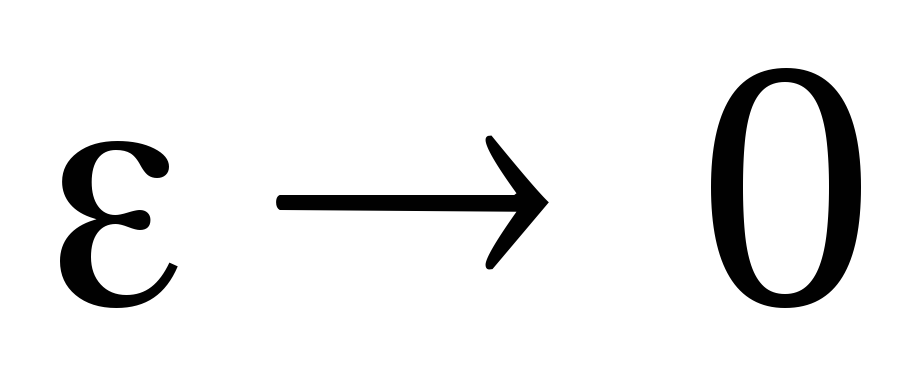
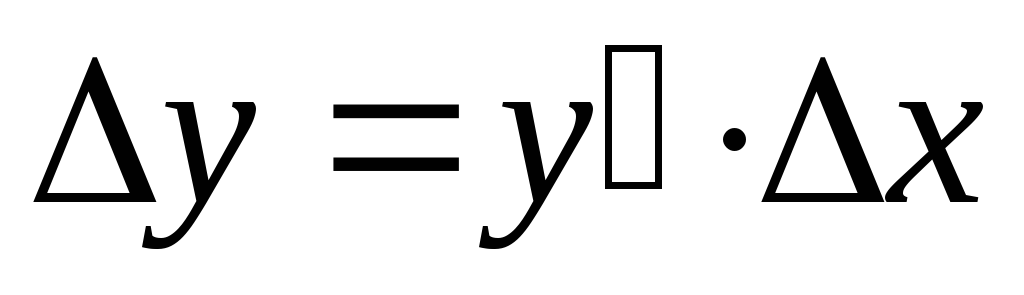
A fő rész a növekmény funkció, lineáris az a növekménye a független változó

. Ez az úgynevezett differentsialomfunktsiiés jelöljükvagy:

.

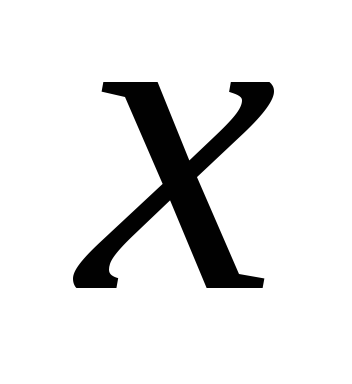
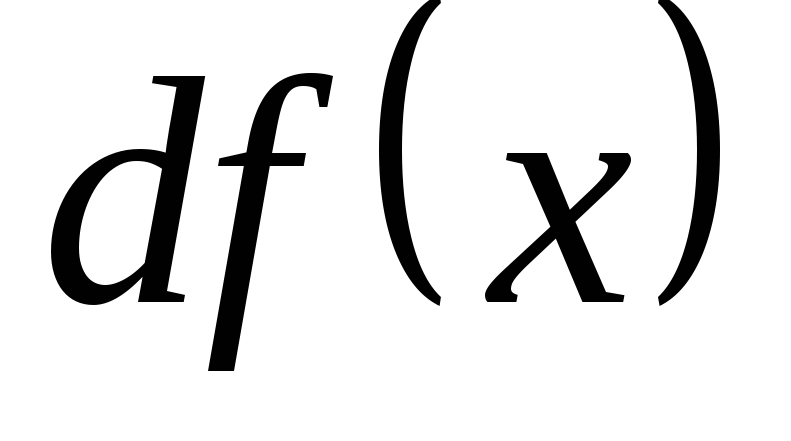
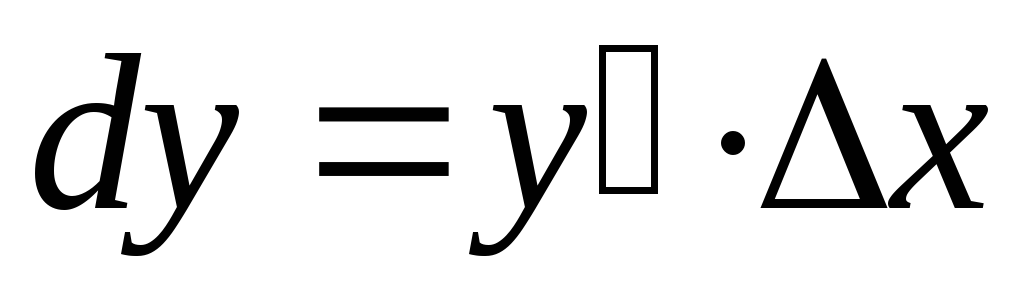
Mivel az. Differenciálmű

, a differenciál a funkció a termék differenciálhányados a differenciál az érvelés:

.

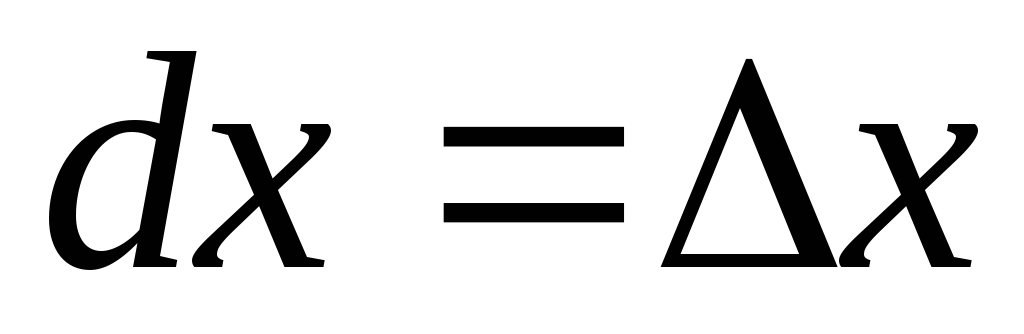
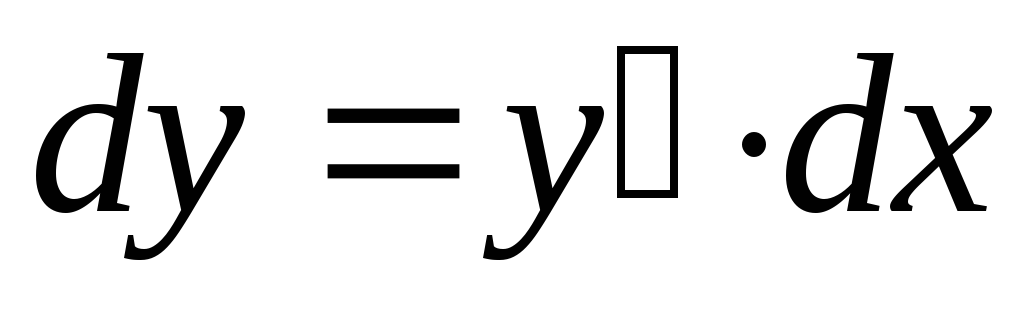
Így annak érdekében, hogy megtalálják a differenciál funkciót, meg kell találni a származékos

és szorozza meg az eltérés a független változó .

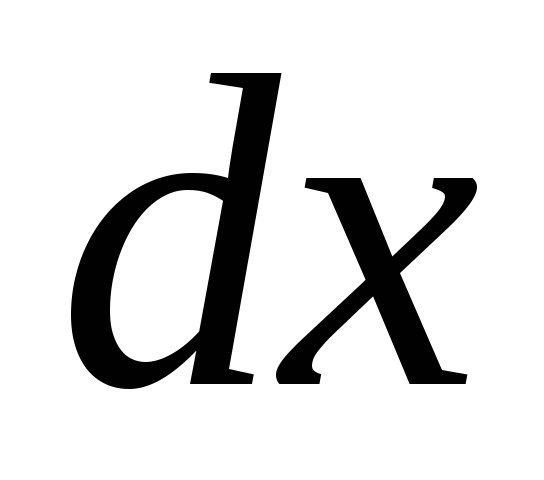
Találja meg az eltérés funkció

.

.

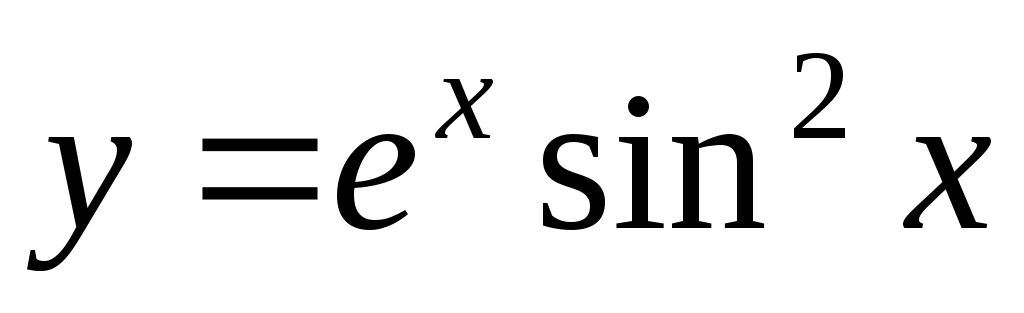
2.4. A használata differenciálszámítás a függvények egy változó

2.4.1. Alkalmazása a származék határértékeinek kiszámítására.

L'Hospital-szabály

Kiszámításakor a határ a függvény határérték helyettesítés érv gyakran vezet a bizonytalanság formájában

,, ahonnan lehetetlen megszabadulni a korábban vizsgált módszerek. Tétel, ismert, mint a L'Hôpital nazvaniempravilo. Ez az egyik fő eszköze a nyilvánosságra hozatala az ilyen bizonytalanságok.

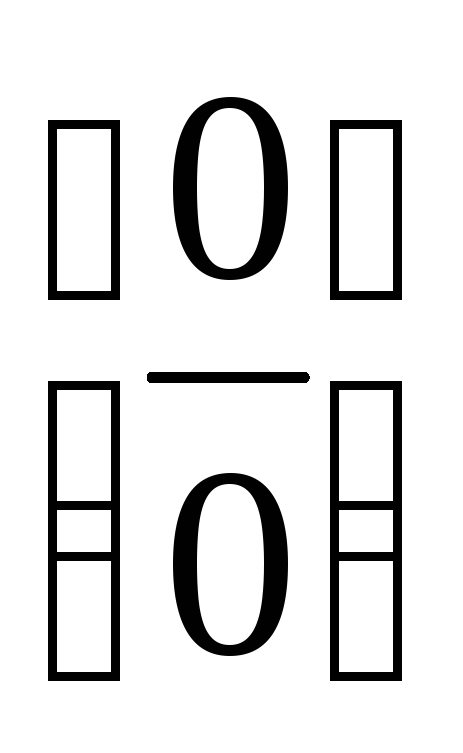
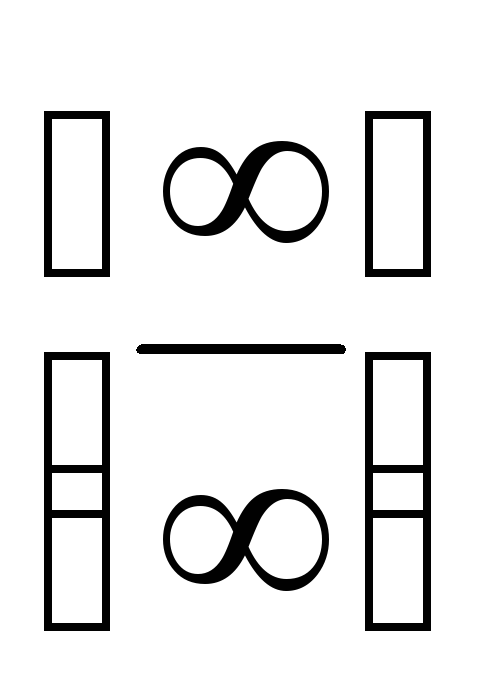
L'Hospital-szabály: Tegyük fel, hogy a szomszédságában

funkciókésdifferenciálható és. haésegyaránt végtelenül kicsi vagy végtelenül nagy funkciók , az

,

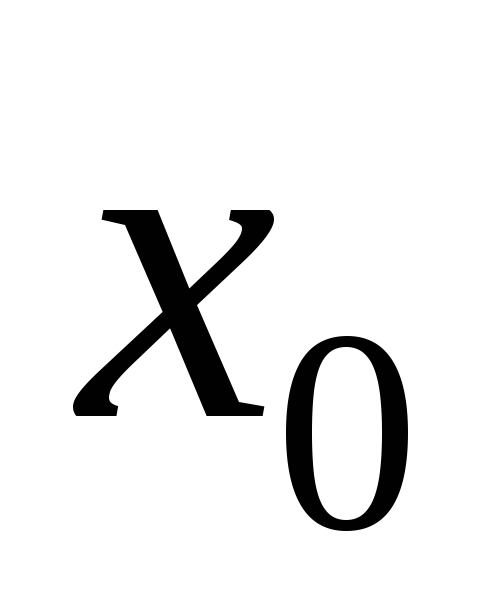
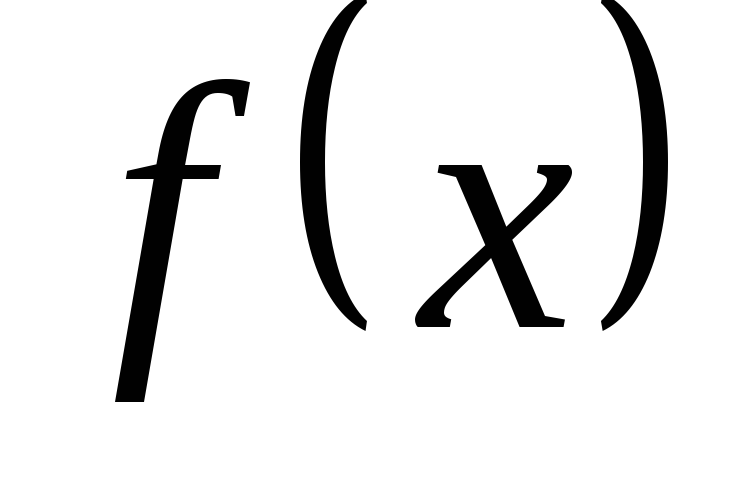
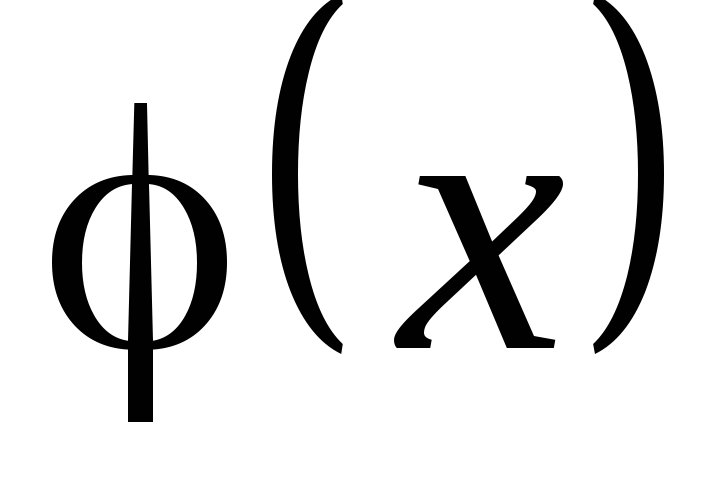
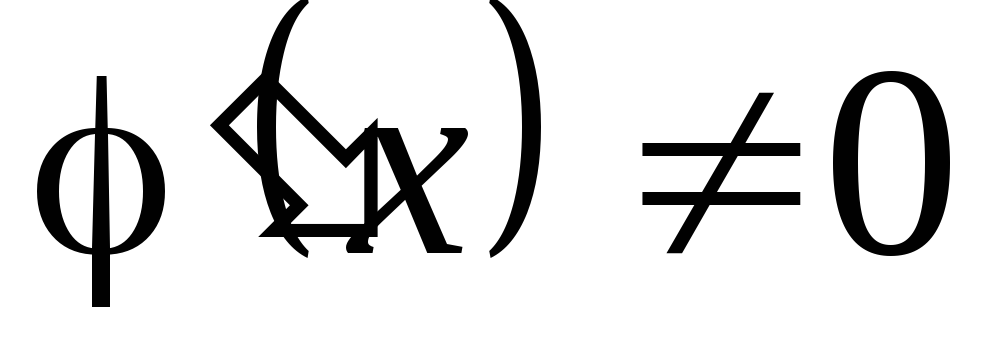
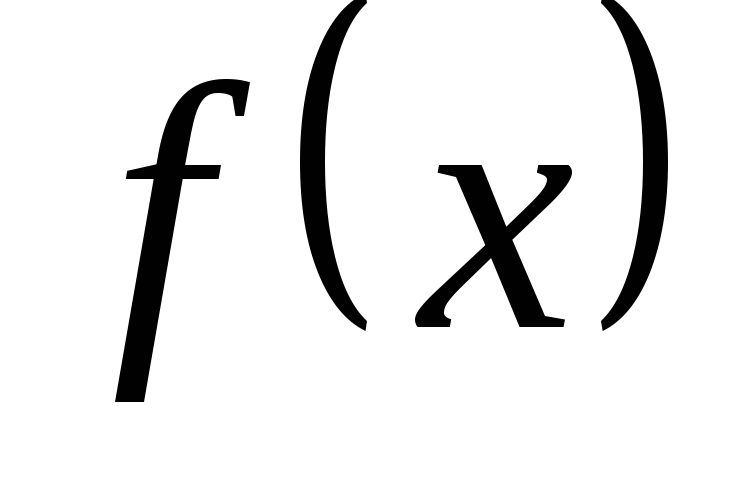
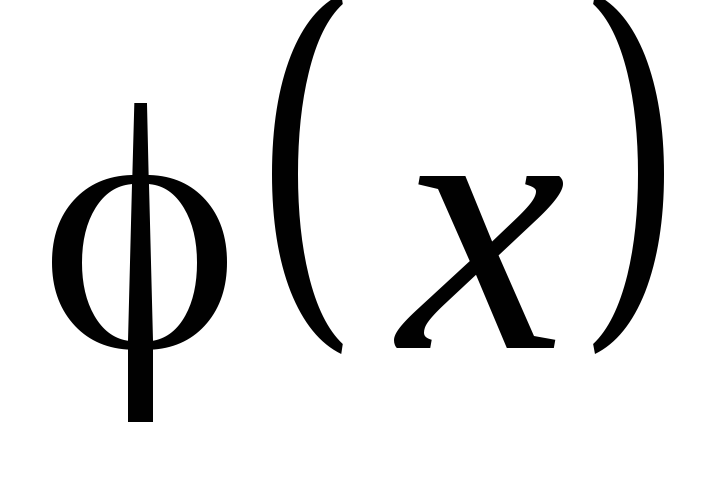
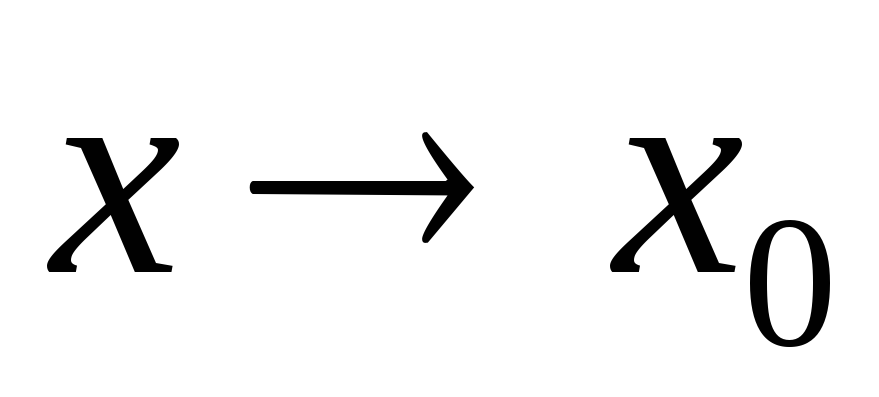
feltéve, hogy határérték-származékok összefüggés áll fenn.

Ez a tétel is érvényes egyoldalú határértékeket, és amikor

.

Bizonyos esetekben a közzététel típusú bizonytalanság

Ez megkövetelheti ismételt alkalmazása L'Hospital-szabály.

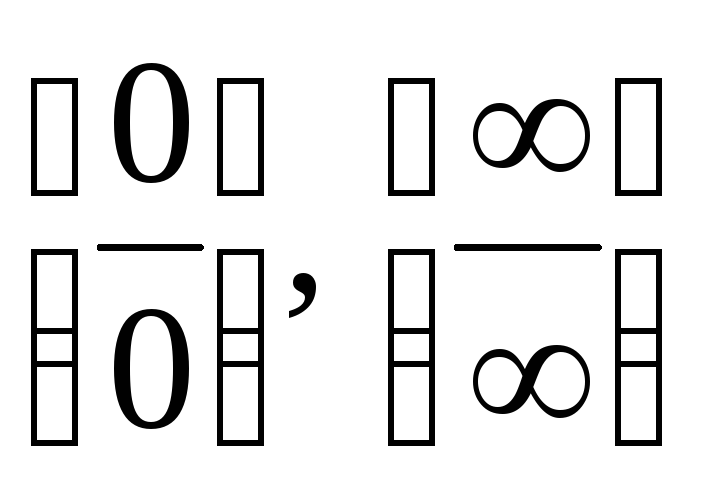
bizonytalanságok

,,,,, csökken a jellegtelen algebrai manipuláció.

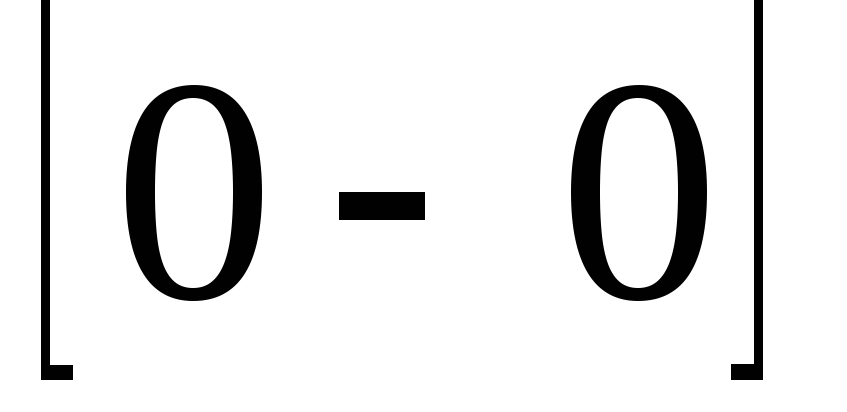
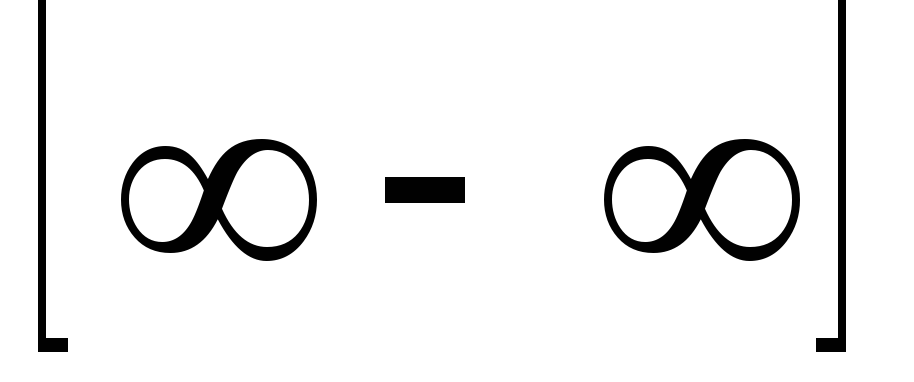
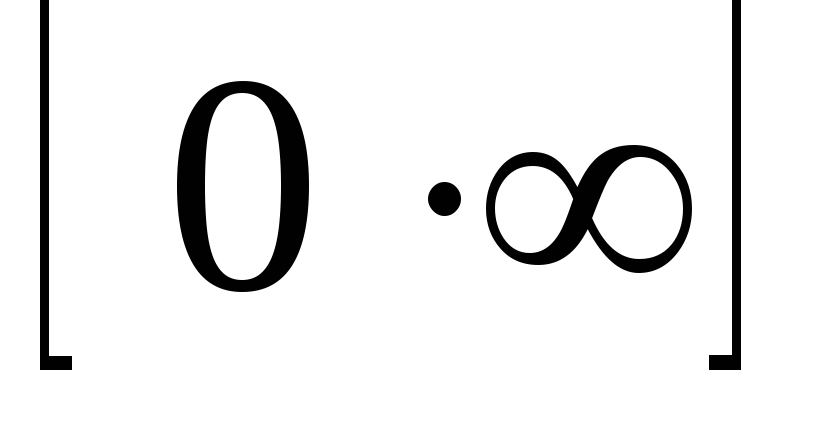
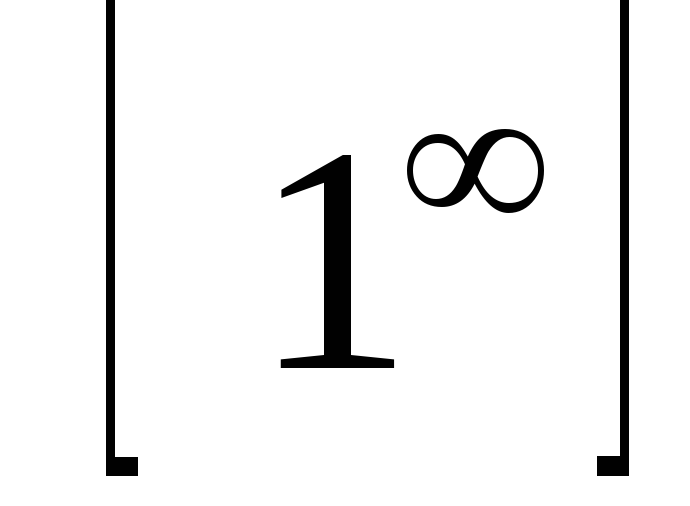
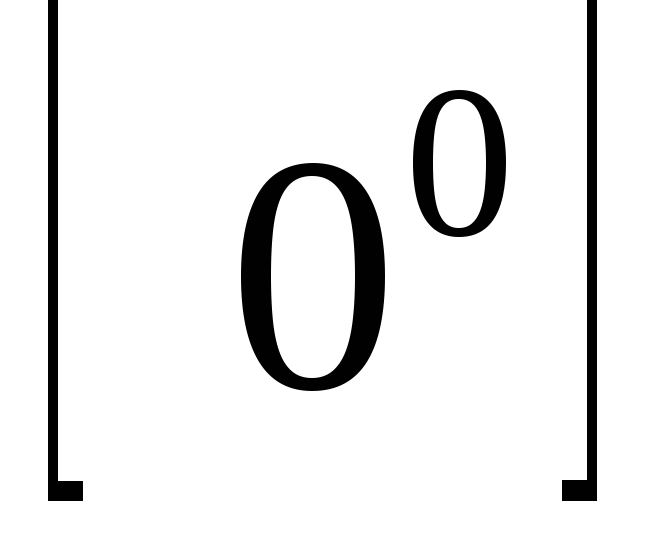
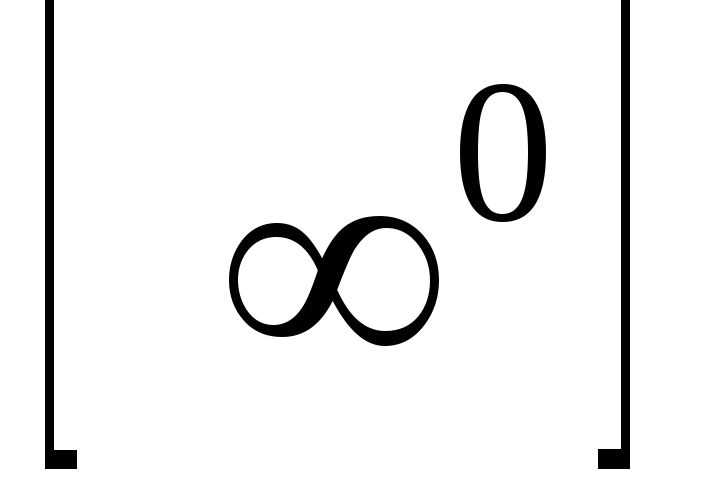
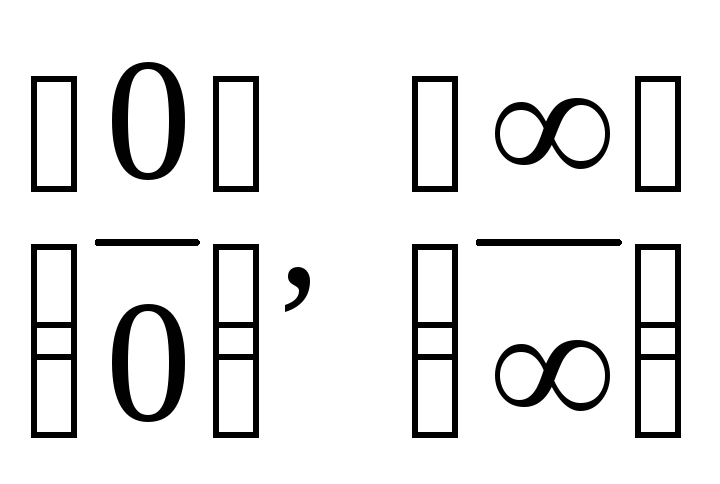
Kiszámításra L'Hospital-szabály határértékek:

.

.

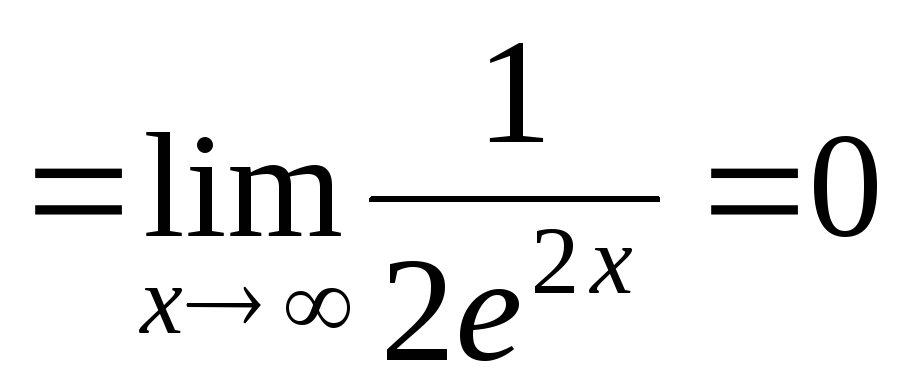
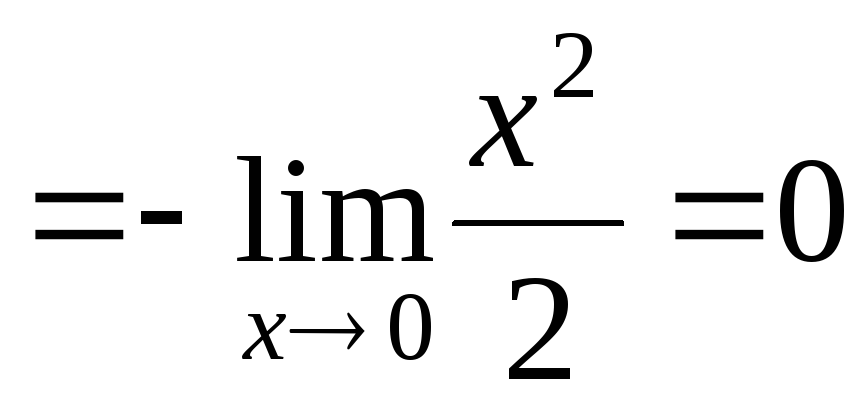
Jelöljük a kívánt határt

és logaritmusát a kifejezést:

;

.

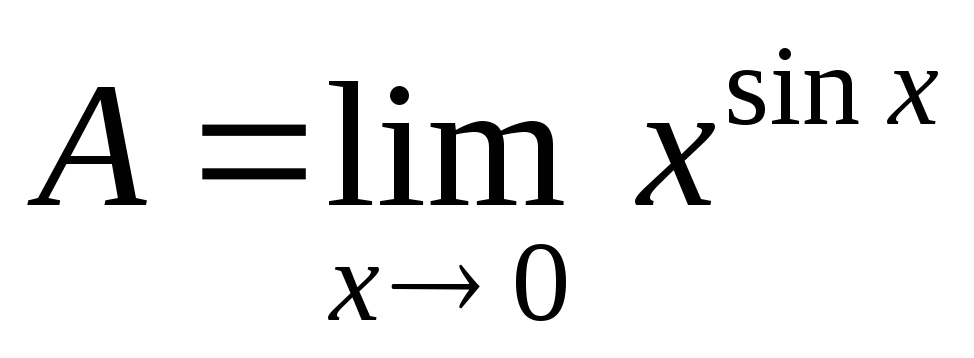
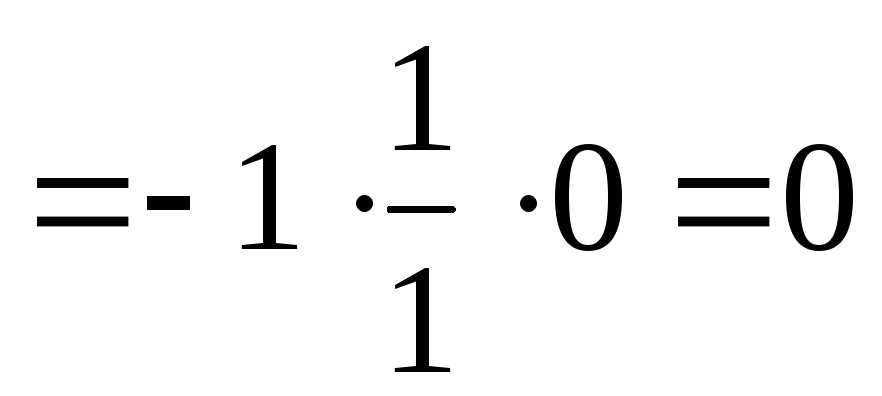
mert

, a kívánt értékre.

Kapcsolódó cikkek

• logaritmikus derivált

• Logaritmikus differenciálódását funkciók

• A származék az exponenciális és logaritmikus függvények