logaritmikus derivált
Ma megyünk a következő szintre ügyességi megtalálni a származékot - tanulmányozza a logaritmikus derivált és származtatott energia-exponenciális függvény. Olvassa ezt a leírás feltételezi, hogy már tudja, hogyan kell megtalálni a származék egyszerű és összetett függvények, összegek, a termékek és a kapcsolatok. Ha valami a fenti okozza a problémát, akkor meg kell felfedezni a téma a „Hogyan lehet megtalálni a származék” és „származék egy összetett funkciót.” Azt feltételezzük, hogy ezek a témák már eltelt.
Vegyük ezt a példát:
1. példa Find a függvény deriváltját
megoldás:
Számos lehetőség megtalálásához származékot ezt a funkciót. Az első - ez a „fej”. Ie festék kezdeni magán-származék, származékos művek és megfontolja, hogy, hogy ... A hátránya ennek a módszernek abban a tényben rejlik, hogy a folyamat megoldások nyúlik nagyon nehézkes frakciók, amely röviden zavaros és hibáznak.
A második lehetőség -, hogy megpróbálja átalakítani a származék (egyszerűsített) funkciót. A mi esetünkben, jó lenne, ha, hogy megtalálják a származékos termék, vagy csak a bal vagy csak a hozzáállás. Ehhez távolítsa el a zárójelben a számlálóban, a kimeneti kapunk egy frakció, amelyben mind a számláló és a nevező polinomok. Különbséget ilyen frakció már lesz könnyebb.
A második módszer a feladat megoldható ....
És végül, a harmadik, és a legegyszerűbb lehetőség -, hogy megoldja ezt a feladatot a segítségével a logaritmikus derivált. Mit kell? Minden banális egyszerű: meg kell, hogy „lógni” logaritmusát mindkét oldalán az egyenlet.
Most emlékeznünk kell logaritmusát tulajdonságokkal, nevezetesen, hogy a logaritmusa a termék az összege logaritmus, és a logaritmusát az arány egyenlő a különbség a logaritmus, azaz
És szükségünk lesz egy másik hasznos tulajdonsága a logaritmus: mértéke a logaritmus lehet venni belőle
Most kell alkalmazni ezeket a tulajdonságokat a funkció
Továbbra is a különbséget. Remélem emlékszel, mi a származék logaritmusa - ha nem is azonnal lásd származék, vagy töltse le a számítógépére.
A differenciálás a jobb oldali nem okoz neked nehézséget, és ezek származékai, azt találtuk, többször is. De a bal oldalon érdemes szólt egy pár szót. Csak írj, hogy - nem elég, mert - ez egy komplex függvény, amely függ. Ezért a származékos kell tekinteni, mint komplex függvények, azaz .
kap
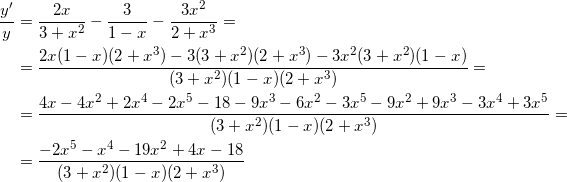
Ie már kialakult, már csak azt kell kifejezni, költözött a jobb oldalon
Mi helyettesíti az érték az állapot és átalakítani, ha átalakítható
A differenciálás alkalmazásával logaritmus a használata kényelmes, ha adott a nehézkes expressziós vagy expressziós szintje. Az első esetben az a logaritmus segít megtörni a kifejezést kisebb részekre, a második -, hogy megszabaduljon a fokozatot.
Lássuk egy másik példa
2. példa Find a függvény deriváltját
megoldás:
„Hang” a logaritmus
Alkalmazása a logaritmus tulajdonságai
A konkrét esetben a mértéke teljesítmény-exponenciális függvények. Ők vannak a földön és mértékben talált. A legegyszerűbb példa a teljesítmény-exponenciális függvény
3. példa Find a függvény deriváltját
megoldás:
Az általunk használt módszer logaritmikus differenciálás
Alkalmazása a logaritmus tulajdonságai a mértéke
A gyakorlatban azonban, mint általában, vannak bonyolultabb gépi exponenciális függvények.
4. példa Find deriváltja
megoldás:
Hang logaritmusok mindkét oldalán
Alkalmazza az ingatlan a logaritmus