Jelek spektrális előállítása
Bármilyen jel bontható komponenseket. Ez a jel az úgynevezett spektrális felbontása. A jel lehet képviseli, mint egy telek a paramétereket a frekvencia jel, például egy diagram az úgynevezett spektrális vagy spektrumú jel.
Spektrumú jel - egy sor egyszerű jelösszetevõket határozott amplitúdójú, frekvenciák és a kezdeti szakaszban.
Ez jelzi a spektrumot, és alakja van egy erős összefüggés: a változás a görbe megváltozását eredményezi színképének, és fordítva, bármilyen változás a spektrum a jel változásához vezet annak alakját. Fontos megjegyezni, mivel a jelek továbbítása egy átviteli rendszer, azok változhatnak, mivel ez azt jelenti, hogy az átalakítás a spektruma.
Kétféle spektrális grafikonok:
- amplitúdóspektrumot diagram;
- spektrális fázisdiagramja.
Amplitúdója a spektrális diagram - megmutatja az összes komponenst az amplitúdója és frekvenciája.
A spektrális fázisdiagram - azt mutatja, az összes komponenst a kezdeti fázisban és frekvenciák.
Bármilyen jel spektrális diagram a spektrális amplitúdók, valamint egy fázis-diagramja, amelyben szerkezet tartalmazhat több komponenst.
Nem számít, hogy milyen a spektrum (amplitúdó vagy fázis), akkor a jelentése, mint amely több vezetéket - alkatrészek. A spektrum a spektrális vonal amplitúdók magassága azonos a jel amplitúdóját komponens, és egy fázistranszfer-spektrum - a kezdeti fázis komponenst. Ezen túlmenően, a spektrumát amplitúdók összes komponens pozitív, és a fázis-spektrum, mind pozitív, mind negatív. Ha az amplitúdó spektrális komponens negatív, úgy ez az modulo amplitúdóspektrumot és fázis spektruma jele komponenst megfordul.
Besorolás spektrumú jeleket.
1. Szerint a típusú spektrumok diszkrét (uralkodott) vagy szilárd.
A diszkrét spektrum, amelyben az egyes komponensek azonosíthatók.
Folyamatos spektrum, aki nem tudja elkülöníteni az egyes komponenseket, mivel közel vannak ahhoz, hogy egyesül egymással.
2. megkülönböztetni tartományban frekvenciaspektrumai korlátos és határtalan.
Spectrum korlátozott, amelynél a teljes energiáját a jel (összes spektrális komponensek) vannak korlátozott frekvenciatartományban (fmax.).
Tartomány korlátlan, amelyben az összes jel energiáját korlátlan frekvenciatartomány (fmax.). A gyakorlatban az ilyen spektrumok korlátozott.
A spektrális ábrázolását periodikus jelek
1. harmonikus rezgés.
Matematikai modell a harmonikus oszcilláció:
u (t) = Ums sin (? st +? s) (11)
Mint látható a matematikai modell, a spektrum a ingadozások harmonikus komponens van jelen, amely a frekvencia? S. A magasság a komponens a spektrum amplitúdója megegyezik az amplitúdó-ingadozások Ums, és egy fázistranszfer-spektrum - a kezdeti szakaszban a oszcilláció s ?. Ezen túlmenően, az építőiparban a spektrum szükséges közötti időben jelet, és a spektrum diagram amplitúdók. Az amplitúdó a spektrum komponenst kell egyeznie rezgési amplitúdó korrekciót az időzítési diagramot.
Meg kell jegyezni, hogy gyakoriságának növelése a jel komponens eltávolítjuk azt a frekvencia tengelyen a nulla (13. ábra).
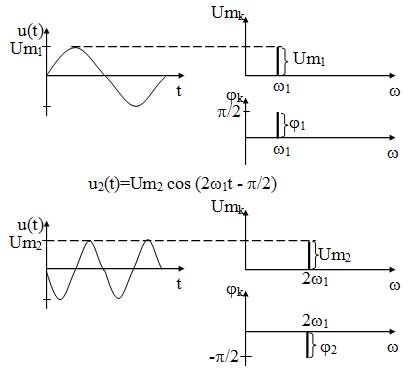
13. ábra - A spektrális ábrázolását harmonikus rezgések
Amint az az ábrákon látható, a spektrum a harmonikus rezgések diszkrét és korlátozott.
2. Az időszakos, nem-harmonikus jelek.
A fő jellemzője a spektrális ábrázolását a jel jelenléte a spektrális komponensek sokaságának a spektrum. Ezek a jelek leírható egy Fourier-sor, amely szerint:
t. e. a jel lehet összege által képviselt az állandó komponens és több harmonikus összetevők.
Átalakítás a sorozat segítségével trigonometrikus tulajdonság
sin (x + y) = sin x cos y + cos x sin y (13)
? Feltételezve, hogy x = k és y = k ct kapjuk:
Mivel ÚMK és? K a paraméterei a sorozat, akkor kijelöli együtthatók
ÚMK bűn. k = ak; UMK cos? K = bk (15)
Ezután a sorozat lesz:
számos paraméter lehet definiálni együtthatók ak és bk:
Az amplitúdó a DC komponensen és együtthatókat lehet meghatározni a jel értéke u (t):

Tekintsük a spektrális ábrázolását az időszakos, nem-harmonikus jeleket egy példa egy periodikus szekvencia négyszögletes impulzusok (PIP).
A következő paramétereket kell kiszámítani, amikor az építőiparban a spektrum:
a) terhelhetőség jel:
b) a konstans értékét komponens:
c) a frekvencia az első harmonikus a spektrum, amely egyenlő a jel frekvencia:
g) az amplitúdó spektrumát harmonikus összetevők:
Az építőiparban a spektrum szükséges megjegyezni a következő funkciókat:
1. Minden harmonikus komponensek frekvencián, amelyek többszörösei az alapfrekvencia (2 1, 3 1, 4 1, stb. ??? ..);
2. A spektrum tartományok:
a) van egy spektrum; STD szirmú jellegű, azaz a spektrum kiosztani sokaságát „szirmok” ..;
b) a számát harmonikus komponenseit a szirmok függ a terhelhetőség és egyenlő q - 1;
c) az amplitúdó a harmonikus összetevők, amelyek a frekvenciák, amelyek többszörösei a munkaciklust, nullával egyenlő;
g) alakja a spektrum boríték jelöljük - szaggatott vonal simán csúcsokat összekötő harmonikus komponensek;
d) az a pont, ahonnan jön a boríték vagy egyenlő 2U0 2I0.
3. a fázis a spektrum:
a) az összes harmonikus összetevők frekvencián, amelyek nem többszöröse a munkaciklust, amelyek azonos magasságúak egyenlő / 2 (90 °) ?;
b) minden harmonikus összetevő egyetlen lebeny ugyanaz az előjele, és a szomszédos ellenkezője.
c) komponensek frekvencián többszörösei a munkaciklus van egy kezdeti fázis nullával egyenlő.
Pip-spektrumokat, ha a kitöltési tényező q = 3 a 14. ábrán látható.
Mint látható a diagramok; STD spektrum diszkrét és korlátlan. Ezért, a spektrum szélessége fogadására frekvenciatartomány, amelyen belül az első két lebeny, hiszen a bennük tartalmazott mintegy 95% a jel energia ..:
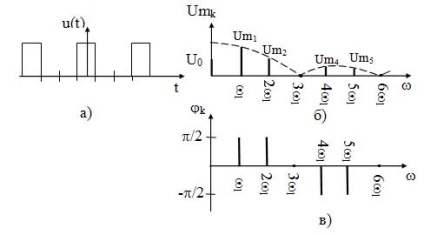
14. ábra - A spektrális képviselete; STD: a) egy idődiagram; b) spektrális diagram az amplitúdók; c) egy spektrum diagram fázisok
Amint látható, a spektrális szélessége körlet interfész pontokat csak attól függ, az impulzus időtartam és független annak időszakban.
3. Nem periodikus jelek.
Mivel a nem periodikus jelek nem tudja kiválasztani a t. K. TA kiszámításához és a telek a spektrum ugyanolyan módszerrel, mint lehetetlen periodikus jelek. Azonban, a tudás a spektrum ezen jelek szükséges, azaz a. K. összes információ jelek nem periodikus. A konstrukció egy periodikus jel spektrumának előállított következő eljárással: szignál mentálisan szakaszos egy tetszőleges időszak, amely építeni ddlya spektrum. Ezután, a szabályozó folyamat hagyta időszakban a végtelenig (?? T) (15. ábra). A frekvencia az első harmonikus, és ennek megfelelően, a távolság a felharmonikus komponensek általában nulla (f1 = 1 / T), úgy, hogy az összes komponens összeolvad egymással és egy olyan folytonos spektrum.
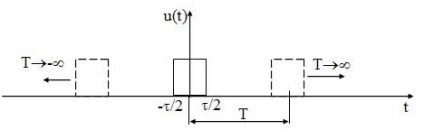
15. ábra - az impulzusjel u (t) és reprezentációja periodikus jel
Az alakja a spektrum boríték jelöljük nem periodikus jelek (folytonos vonal) (16. ábra).
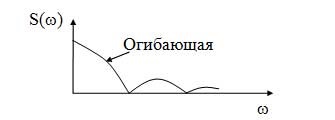
16. ábra - A spektrális chart nem periodikus jel
A Fourier-sor ilyen jelek, továbbá nem lehet rögzíteni, t. K. Ebben az esetben, az amplitúdó a DC komponensen és az együtthatók ak és bk nulla. Ebben az esetben a jel értéke bármikor is nulla, ami nem igaz. Ezért az ilyen használata a jelek Fourier-transzformáltja:
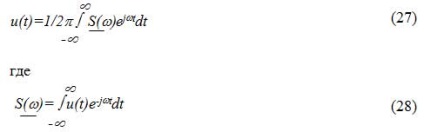
Nagysága S (?) A komplex spektrális sűrűség u (t) jel periodikus. Ez egyenlő:
ahol az amplitúdók a spektrális sűrűség S vagy nem periodikus jel amplitúdója spektrum, a (?)? (?) - fázis spektrum periodikus jel.
A spektrális sűrűsége amplitúdóinak aperiodikus jel bármely frekvencián. egyenlő a teljes amplitúdó található egy kis sávban. A frekvencia a közelben. újratervezi 1 Hz.
Időzítés diagramok és spektrális amplitúdója sűrűséget téglalap és háromszög impulzusokat a 18. ábrán látható:
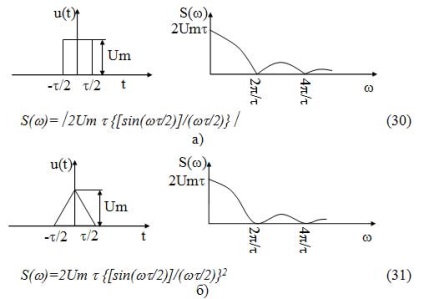
18. ábra - A spektrális ábrázolását nem periodikus jelek: a) egy négyszögletes impulzus; b) egy háromszög alakú impulzus