Döntés statikai problémák
Gorbaneva Larisa Valerevna
adjunktus fizika FESUH
Kihívásaira statika
Statika tanulmányok egyensúlyi állapotok a szervezet tevékenysége révén az alkalmazott erők. Egyensúlyi egy nyugalmi állapotban vagy egyenletes mozgás vagy elfordulás. A következő típusú egyensúly: stabil, instabil és közömbös.
Stabil egyensúlyi állapotot. ha a test következtetni stabil egyensúlyi, az erő jelenik meg, akkor visszatér az egyensúlyi helyzetébe. Stabil egyensúlyi érték megfelel a minimális potenciális energia.


A kényes egyensúlyt. ha a test, hogy visszavonja a labilis egyensúlyi olyan erő, amely eltávolítja a test egyensúlyi helyzetét. Instabil egyensúlyi érték megfelel a maximális potenciális energia.
Közömbös egyensúlyt. Amikor a test eredő állapotát semleges egyensúlyi további erők keletkeznek.
Mert egyensúly megköveteli, hogy a vektor összessége gyakorolt erők a test nulla sem.
Az egyensúlyi állapot lehet írni másképp. Ha kiálló összes erők a kiválasztott X és Y tengely, az egyensúlyi állapot válik:
Ezek az egyenletek az úgynevezett egyenletek egyensúlyi anyagból pont a nyúlványok.
Ha a test tengely körül forognak, akkor nem elég egyensúlyt egyenlő nullára a kapott minden erő.
A forgó intézkedés az erő nem csak attól függ a méret, hanem a távolságot az erő vonalára, és a forgástengely.
A hossza a merőleges levonni a forgástengely a hatóirányának erő, az úgynevezett váll erőt. Leggyakrabban váll betűvel jelöljük d.
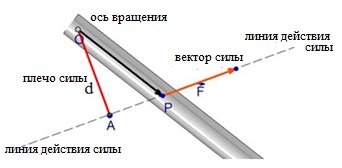
tápegység modul terméket a váll d egy Power Point
. Az egység a pillanatnyi erő - H ∙ m.
Abban a pillanatban, az erőnek, hogy forgassa a test mértani tengely körül az óramutató járásával ellentétes pozitív óramutató járásával megegyező - negatív.
Ha a szervezet számos erők található ugyanabban a síkban (síkban rendszer erők), a modul a kapott pillanatában erők képest a kiválasztott pont O egyenlő az algebrai összege az egyes pillanatok:
Szabály pillanatok: a test, amelynek egy rögzített forgástengely egyensúly van, ha az algebrai összege pillanatok ható erők a test ezen tengely körül nulla.
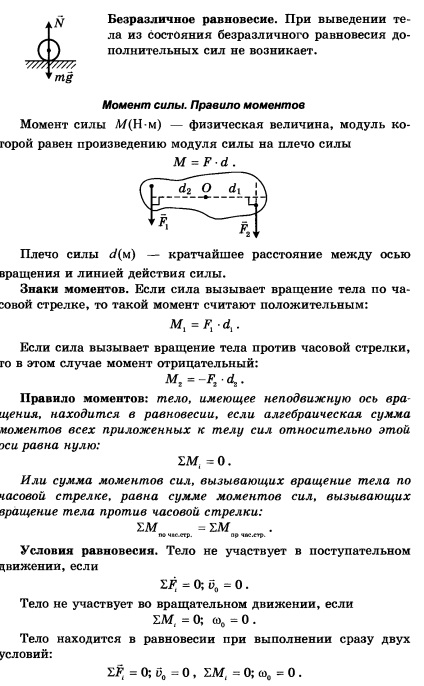
Összege, vagy a pillanatok kiváltó erők a test forgását az óramutató járásával megegyező irányban, egyenlő az összege pillanataiban erők okozó szervezet az óramutató járásával ellentétes forgatás:.
Az egyensúly a szervezetben szükséges két feltétel:
A vektor összessége ható erők a test nullával egyenlő.
Az algebrai összege nyomatékok bármely tengely körüli nulla.
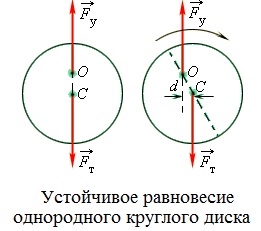
Egy test, amelynek rögzített forgástengelye, mindhárom lehetséges egyensúlyt. Közömbös egyensúly akkor jelentkezik, ha a forgástengely áthalad a tömegközéppont. Ha a stabil és instabil egyensúlyi súlypontja a függőleges vonal áthaladó forgástengely. Itt, ha a súlypont alatt a forgástengely, az egyensúly stabil. Ha a tömegközéppontja felett található a tengely - instabil egyensúlyi állapot (lásd ábra.).
Egy különleges eset az egyensúlyt a szervezetben a támogatást. Ebben az esetben, csatolt nem egy ponton a rugalmas erő a támasz és elosztva a szervezetben bázis. A test egyensúlyban van, ha a függőleges vonalat húzott át a súlypont a test áthalad a csapágy terület, azaz a. E. belül a hurok által kialakított összekötő vonalak pontok támogatást. Ha ez a sor nem metszi az érintkezési felület, a test meg van döntve. Egy érdekes példa az egyensúly a szervezetben a támogatás a pisai ferde torony az olasz város, amely a legenda szerint Galileo a tanulmányban használt törvényeinek szabadon eső testek. A torony henger magassága 55 m és a sugara 7 m. A torony tetején van döntve a függőleges 4,5 m.
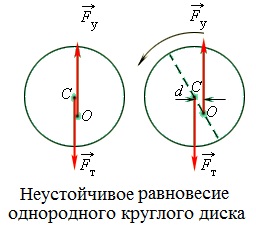
A függőleges vonal át húzott a tömegközéppontja a torony, metszi a bázis körülbelül 2,3 m-re a központtól. Így a torony egy egyensúlyi állapot. Egyensúly megbomlik, és a torony fog esni, amikor a felső eltérés a függőleges elérheti a 14 m. Úgy tűnik, ez fog történni hamarosan.
A problémák megoldására a statika használhatja az algoritmust.
1. Készíts egy rajzot az összes ható erők a test (vagy rendszerek a szervezetben), amelyek egy egyensúlyi helyzet, válasszon egy koordináta-rendszerben, és határozza meg az irányt koordinátatengelyeken.
2. testet, amelynek nincs forgástengelye, az első feltétel van írva vektor formában egyensúlyi. majd rögzítse a az egyensúlyi állapotot a nyúlványok a koordinátatengelyeken és egy olyan egyenletet skalár formában.
3. A test, egy fix forgástengely meg kell határozni a vállán minden erő ezen tengely körül, és egy második egyensúlyi állapot (általában utal).
Ha a probléma a feltétellel, hogy a test forgástengelye nem rögzített, akkor kell használni az egyensúlyi feltételeket. Ehhez válassza ki a tengely, amely körül célszerű meghatározni a nyomaték (a pozícióját a forgástengely úgy kell megválasztani, hogy áthaladt a legnagyobb számú cselekvési irányvonalat ismeretlen erők), amely meghatározta a vállát, és írja be az egyenletet kifejező második az egyensúlyi állapotot.
4. Hogy oldja meg a kapott egyenletrendszert, hogy meghatározzuk az ismeretlen mennyiségek.
Tekintsük a példát problémák megoldására a használata a fenti bemutatott algoritmus.
1. példa Egy henger súlyú m = 150 kg visszamarad egy ferde sík szalag, az egyik oldalon van felszerelve egy ferde síkban, és a többi irányított síkjával párhuzamosan. Keresse meg a húzóerő a szalagot. A dőlésszög a síkja α = 30 °.
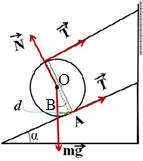
Határozat. A probléma megoldható segítségével akár csak az első az egyensúlyi állapotot, vagy csak a második.
1 módja. Az első az egyensúlyi állapotot. Írunk az összessége erők. ahol T - szalagfeszítő erő, N - padló reakció erő, mg - henger gravitációs erő.
Vegyük a vetülete erők a OX és OY. Közvetlen a OX tengelye mentén a szalagot húzóerő, és OY tengelye merőleges a kiválasztott tengely és az irányt az erő N.
Megoldása kapott egyenletrendszert T kapjuk:
2 módszer. Amelyet általában pillanatok egy tengely körül ponton áthaladó A.
Váll gravitációs d1 határozzuk meg a háromszög OAB ahol OA = R. AOB szöge egyenlő a dőlésszög a gépet. Ezután d1 = R · sinα.
Váll öv húzóerő d2 átmérője a henger, vagy d2 = 2R.
Ezután a jogállamiság pillanatok A tengely körül:
Ebből az egyenletből, megkapjuk:
2. példa Egy homogén vékony nyaláb AB 100 kg-os támogatja egyik végén egy sima vízszintes padlóra, és a másik - a sima sík ferde szögben 30 ° a vízszinteshez képest. A támogatott végén a fény a terhelést kötelet átvetve C blokk (lásd. Ábra.). Határozza meg az áruk tömege és a padló reakció erő normális és ferde sík. Elhanyagolás súrlódás a blokkban.
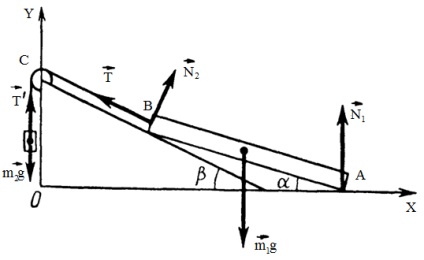
Határozat. Tekintsük ható erők a gerenda: M1G - a gravitációs erő; N1 és N2 normál padló reakció erő és a ferde sík; T - erő kötélfeszesség.
Befolyása alatt ezek az erők a fény egyensúlyban van. Írja gerenda első feltétele az egyensúly:
Választásával az irányt a OX és OY tengelyek (mint látható) kiálló rájuk egyenletet, megkapjuk
Mi író nyaláb a második feltétel az egyensúly tekintetében egy átmenő tengely B pont: M1 M2 = 0.
Behelyettesítve a kifejezéseket az M1 és M2 szerezni
hol. Behelyettesítve számszerű adatok megszerzése N1 = 490N.
Behelyettesítve ezt a kifejezést az egyenlet. és a következő egyenlet segítségével
Mivel a terhelés az egyensúly, akkor. és.
Aztán. Behelyettesítve számszerű adatok m2 = 25kg.
Behelyettesítve a kifejezés a T lelet értékét N2.
3. példa létra 4m felelős a tökéletesen sima fal szögben 60 ° a vízszinteshez képest. A súrlódási tényező közötti padló és lépcsők 0.33. Milyen messzire a létrát mászni a személy előtt, a létra elkezd csúszni? Súly létra elhanyagolt.
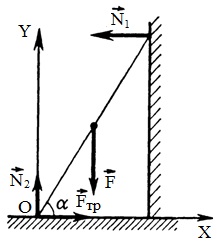
Jelöljük az összes ható erők a létrán: N1 és N2 - reakció erő a fal és a padló, F - az erő az emberi nyomás a lépcsőn; FTP - a súrlódási erő.
Csúszó lépcső lehet tekinteni, mint egy kombinációja két mozgás: rotációs (pont körül O) és előre (az irányba elleni X tengely).
Írunk az első az egyensúlyi állapotot létra:
Vetítjük a kapott egyenlet
Írunk a második feltétel a létra képest az egyensúlyi állapot A:
Ezt figyelembe véve, átírhatjuk a feltétellel létra egyensúlyi pont körül O.
Ebből az egyenletből.
Az egyenlet az első létra egyensúlyi állapotát és meghatározása, valamint a súrlódási erő talál N1 = uF.
Behelyettesítve a numerikus adatokat S≈2,3m.
Vizsgálat évfolyamon 9.
F.9.1. Homogén gerenda 6 méter végükön van két pillérre épül. Ahhoz, hogy a sugár a parttól 2 m-re a jobb vége a felfüggesztett teher tömege m = 750 kg. Tömeg gerenda 120 kg. Milyen erő gerenda a terhelés nyomást a megfelelő támogatást?
F.9.2. A földön fekszik egy nyaláb 90 kg tömegű. Milyen erőt kell kifejteni, hogy szüntesse meg a gerendát az egyik végén?
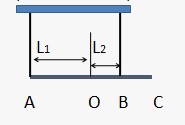
F.9.3. Beam 140kg tömeg van felfüggesztve két kötél. Határozzuk meg a húzóerő kötelek, ha L1 = 3m, L2 = 1m.
F.9.4. Ha csatlakoztatni két rakomány tömegek 2m, és m egy súlytalan rúd L hosszúsága = 3m. amint az ábrán látható, akkor, hogy a rúd maradt egyensúlyi, meg kell lógott egy olyan ponton O található x távolságban tömege 2m. Keresse meg a távolságot x.

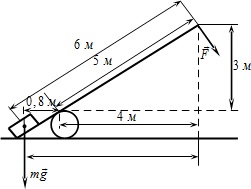
F.9.5. Alatt a gravitáció hatása mg terhelés és kar F erő, az ábrán látható, ez az egyensúlyban. Az erő vektor F merőleges a kar. A pontok közötti távolság, amelyeken az erő és a forgáspont, és a nyúlvány E távolságok a függőleges és a vízszintes tengelyen az ábra mutatja. Modul keresés gravitációs ható terhelést, ha az F erő 120 N modul.
F.9.6. A kar végeihez a lefelé irányuló erő, és 6 H 4 N. A támaszkodási pont található, 5 cm közelebb van az egyik kar végén, mint a másik. Milyen hosszú (cm) a kar, amikor ez az egyensúly?
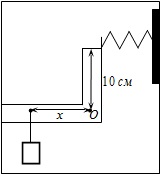
F.9.7. Lung kart komplex alakja a forgáspont egy ponton O (lásd. Ábra) van felfüggesztve egy 2 kg-os, és egy rugó kapcsolódik, a másik vége, amely csatlakozik a rögzített falra. A kar egyensúly van, és a feszültséget a rugóerő 15 N. bizonyos távolságra a forgási tengellyel X felfüggesztett teher, ha a távolság a tengely a kapcsolódási pont a rugó 10 cm.
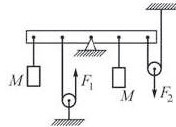
F.9.8. Az egyensúly a vasút révén két azonos terhelések súlytalan blokkok mindegyikének tömeg M a témára dobott egy balra blokk jobbra blokk és a tengely kell alkalmazni függőleges erők F1 és F2 (lásd. Ábra). A távolság a fekete pont a vasúti ugyanaz, nincs súrlódás, nem nyújtható fonalat. Mit lehet vitatkoztak erők F1 és F2.
F.9.9. A rendszer a tömegek m és M, és az azokat összekötő fény nyújthatatlan fonál a kezdeti pillanatában nyugalmi átmenő függőleges síkban a a gömb középpontja rögzített. Terhelés m értéke az A pontban a tetején a gömb (lásd. Ábra). Során rakomány mozgását alakult m elválasztjuk a felületi a gömb rajta áthaladó íven 30 °. Keresse m tömegű, amikor M = 100 g. Méretek terhelés m elhanyagolhatóan kicsi összehasonlítva azzal a gömb sugarának. Friction elhanyagolt.
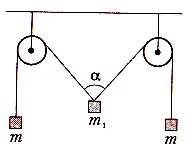
F.9.10. Ahhoz, hogy a végeket az izzószál, átvetve két blokk, két azonos terhelés felfüggesztett tömeget 5 kg. Mi a teher súlya van m1. amikor egyensúlyi α = 120 °?
F.9.11. Stairway fekszik egy függőleges fal és vízszintes padlón. A súrlódási együttható közötti a létrán, és a fal 0,5. között, valamint a padló és a lépcső - 0.4. Határozzuk meg a legkisebb hajlásszöge a létrát, ami még lehet az egyensúlyt.
F.9.12. A rúd súlyú 9 kg és 1 m hosszúságú fekszik két támasz. Az egyik támogatja a bal végén a rúd, és a másik található a parttól 10 cm-re a jobb oldali végén. Milyen erő hat az egyes fő pillére? Válaszul rögzíti a különbség erők.
F.9.13. Acél rúd súlya 6 kg van beágyazva az egyik végfal, és támogatja a pont, A és B; a másik végén a C pont van függesztve, súlya 36kg. Keressen egy nyomóerő a támogatást és B pontok, ha a rúd hossza 80 cm. és a hossza a kinyúló rész 60 cm.
F.9.14. Lépcső súlya 1,5 kg dőlve a függőleges fal szögben 300. A súlypontja a létra található 1/3 a hossza a felső végén. Ahhoz, hogy a felső végén a létra nem nyomást a falon, hogy a közepén a lépcső szükséges alkalmazni erő vízszintesen irányul. Értékének meghatározásához ez az erő.
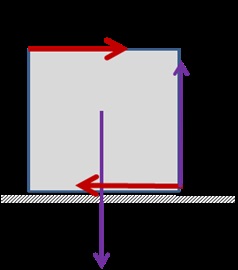
F.9.15. Mi az a minimális vízszintes erőt lehet megdönteni a széle kocka, fekvő, vízszintes síkban?
Kapcsolódó dokumentumok:
és szeptember 1. szeptember 8 ETO 531,2 resheniyazadachpo art példákat tartalmaz: meghatározó kapcsolatok reakciók lapos. SZÁMÚ PROFIL POSTATIKE. SZÜKSÉGES RESHENIYAZADACH 1. Kommunikáció és. kapcsolatok) A tanulmány egy merev resheniizadachpostatike.
idő-méretek, grafika, és így megoldásokat. d. dinamikus és statikus (8 h) koordináta módszerrel resheniyazadachpo mechanika. Resheniezadach az alapvető törvényeket.
Szilárd egyensúlyi körülmények között. resheniyazadachpostatike algoritmus. Példák resheniyazadach. Június 4 2.3 általánosítva ismétlés. 4.1 A törvények elektrosztatika. Alkalmazása az algoritmus resheniyazadachpostatike a kölcsönhatások elektromosan töltött testek.
Munka tananyag
élet feladatokat. STAGE RESHENIYAZADACHPO FIZIKA megértése problémát nyilatkozatot. Ez. energiát. A teljes mechanikai energia. Statikus és hidrosztatikai (1 óra) egyensúlyi körülmények között. mechanikai energiát 9,1-9,45 (1) január 12 statikai és hidrosztatikai 10,1-10,26 (1).