binomiális együtthatók
Ez nagyon fontos alkalmazás fogunk összpontosítani a binomiális együtthatók, vagy inkább azok kiterjesztése tetszőleges értéket az indexbe. Előfordul, hogy egy téma az irodalomban az úgynevezett „kiterjesztett Pascal háromszög”, mert a bővítés a binomiális együtthatók jár kiterjesztése Pascal háromszöget, amely ezeknek a tényezőknek, valamint itt figyelembe a függvény (1 + z) n (pontosabban annak terjeszkedését sorozat) nevezik binomiális a közelben.
A tulajdonságai binomiális együtthatók és bizonyítani az alapvető azonosságok, ebben a szakaszban nem áll rendelkezésre, beszélünk róluk csak a keretében generátorfüggvény. Feltételezzük, hogy az olvasó ismeri az alapvető rendelkezéseinek kombinatorika, vagy legalább találkozott velük a valós életben. Végtére is, a matematika körülvesz minket minden oldalról. Számok, minták és különböző kombinációkban bárhol megjelenhet: az út során, hogy a boltban, kiszámítjuk a nyerési esélyeket a kaszinóban, a kontroll elmélet és még futurisztikus előrejelzéseket. Általában mindenki tudja, hogyan kell számolni. De néha kombinatorika bonyolultabb, mint amennyi szükséges a mindennapi életben. Például kiszámításakor az entrópia egy komplex fizikai rendszer, ha kiszámításához szükséges számú érvényes konfigurációk megfelelő fizikai modell. Tehát a fejlett binomiális együtthatók csak a releváns tudományos, nem hétköznapi számításokhoz.
alapvető meghatározások
Itt van egy kis megálló a definíciók és jelölések, a félreértések elkerülése végett. Készítette az olvasó kihagyhatja ezt a lépést.
Binomiális együttható jelöljük. vagy (ami gyakran előfordul az orosz irodalomban).
Nézzük csak meg néhány szimbólumok. A helyes megnevezése a binomiális együtthatók nem. Mindkét tanítják a magyar iskolákban (és egyetemek) is. Sajnos, nem tudom, hogy miért tartozik gyakrabban használják kijelölése. és a világ többi részén -. Ezért kérjük, vegye figyelembe, hogy ha írsz egy cikket a magyar magazinok, meg fogod érteni, hogyan ezek a tényezők, amelyeket nem azonosítottak és megfelelően javasoljuk, hogy írjon a külföldi magazinok.
Olvassa el a karakter sok szempontból „a kombinációk száma n k», vagy egyszerűen „n-ből k», valamint hogy „a választás k n». Értelmében ezek a kifejezések zárják egy kombinatorikus értelmezése ez a karakter - számos módon lehet választani k tárgyak n különböző tárgyakat, és sorrendje nem fontos. Például, a két elem, amely több tíz módon lehet választani:
Általában ismert, hogy
A folyamat során a számítástechnika, nem kell figyelembe venni felesleges faktoros, akkor azonnal csökkenteni része a tényezők:
Ebből a képletből és épít a jövőben. Hogy ez a helyes meghatározás a binomiális együtthatók. A n szám az úgynevezett felső index és a K - alacsonyabb. Összhangban a kombinatorikus értelmezése n és k kell lennie nem negatív egész szám. A kihívás az lesz, hogy szélesítse a definíció önkényes n értékét.
Binomiális együtthatók, rendezett egy speciális módon, hogy egy Pascal háromszöget.
A XVII századi francia matematikus, fizikus és filozófus Blez Paskal először az ő „Értekezés a számtani háromszög” részletesen ismertetjük a tulajdonságokat a háromszög is (bár a háromszög megtalálható a művek más matematikusok sokáig Pascal).
Beépített ez a nagy háromszög nagyon egyszerű:
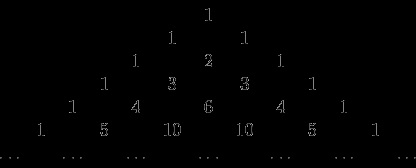
Szélei mentén a háromszög egységek vannak elhelyezve, és tetszőleges számú állva nem a szélén, az összegeként számított két szám található a bal felső és a jobb felső sarokban. Például, 10 = 4 + 6. vagy 1 + 3 = 2. Így beszélünk Pascal háromszöget annak köszönhető, hogy az a tény, hogy az imént alakult binomiális együtthatók:
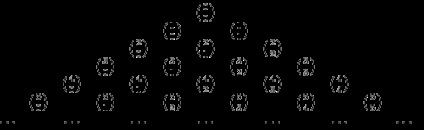
A mi szempontunkból (és az egyszerűség kedvéért) jobb felvenni a háromszög, igazítva a bal szélén:

Nullák jelennek meg, mert nulla a számlálóban (ha k> n). Megjegyezzük, hogy az egységek kerülnek a nulla oszlop, mint
A számláló a termék számának nulla elemek definíció szerint egyenlő 1. A képlet helyes minden (beleértve a komplex) n.
Nos, egyre közelebb vagyunk, hogy tanulmányozza a binomiális együtthatók minden n. A kiterjesztés először olyannak kell lennie, hogy a képlet ugyanaz maradt (az egyszerűség), másrészt, Pascal háromszögben binomiális együtthatók (negatív index értéke), nem szabad elveszíteni az alapvető tulajdonság:
beolvassa, hogy a szám a sejtben (n, k) az összege a felső és bal felső (ha a szám a bal igazítva).
Harmadszor (a legfontosabb), kell, hogy maradjon tisztességes binomiális tétel, akinek nyilatkozatát idézni a következő bekezdésben.
binomiális tétel
Ez a kifejezés is nevezik a binomiális tételt. Binomiális együtthatók és Newton nevezzük binomiális együtthatók.
Most, a binomiális tétel és Pascal háromszöget, ki lehet számítani, például (a harmadik háromszög zajlik)
Ez a weboldal generáló funkciókat, így van ez a tétel csak az érdekli, hogy a pozíciót. Írunk a generáló függvény az alábbiak szerint:
A bemutatott szekvencia generáló függvény generálja a binomiális együtthatók egy felső index egyenlő n-nel. Felső index az összeg felírható egyenlő ∞. ez nem változtat semmit, ha n egy nem negatív (miért?). Megjegyezzük, hogy a szubsztitúció z = 1 ad egy figyelemre méltó személyazonosságát (száma végleges, így a helyettesítés érvényes):
ami azt mutatja, hogy az összeg az összes számok az N-edik sorban Pascal háromszög egyenlő két, hatványát n.
Ez az expanzió a függvény (1 + z) n számos összhangban van a Taylor formula, amelyekkel összhangban a együtthatóit Z, k egyenlő
Hadd emlékeztessem önöket, hogy ez a funkció sorfejtéssel konvergál a | z |<1 (когда n произвольно). Эта функция также носит название «Биномиальный ряд».
kiterjesztés
Most mi érdekli választ arra a kérdésre, hogy akkor meg tudja akadályozni a binomiális tétel, hogy az n egész negatív? Tudod, a Pascal-háromszög kiterjeszti a „fel” az egyetlen módja, ha azt akarjuk, hogy megőrizze alapvető tulajdonságait:
ugyanabban az időben. Tekintsük a negatív sorban több:

Például mínusz az első sorban a háromszög lehet csak úgy, és nincs más út, mert. míg a maradék elemek kiszámítása kifejezetten:
Melyek a speciális binomiális együtthatók? Annak érdekében, hogy állapítson meg egy sor egyszerű frakciók. Például,
Most ebből a képlet az egész negatív binomiális együtthatók alapján nem helyzetük a háromszög, de a helyes meghatározás:
Ez a képlet is összhangban a bővítés ezt a funkciót a Taylor-sor esetében | z |<1.
Gyerünk. A gyakorlatban, hasznos lehet racionális kitevőket, például, úgy a binomiális sor, hogy n = 1/2.
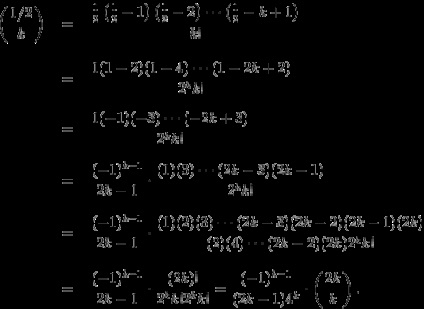
Ez a képlet ad nekünk arra, hogy állapítson meg számos funkciót
Hasonlóképpen (hagyjuk a részletes levezetés az olvasó)
és ez viszont lehetővé teszi, hogy rögzítse egy hasznos generáló függvény:
Beszélünk számos binomiális és helyét az elmélet a generáló függvények. Különleges esetekben a binomiális index: n - egy egész szám, és n = ± 1/2.