Az állapottér
Mivel a tulajdonságok a rendszer által kifejezett értékek kimenetei, a rendszer állapota lehet meghatározni, mint egy vektor értékeit kimeneti változók Y = (y1. Ym). Korábban említettük (lásd. Kérdés №11), hogy az alkotóelemek között a vektor Y, amellett, hogy közvetlenül a kimeneti változókat tűnik önkényes tőlük.
A rendszer viselkedését (a folyamat) is képviselteti magát a különböző módon. Például amikor m kimeneti változók lehetnek a következő folyamat alkotja a képet:
o A táblázat formájában kimeneti változók diszkrét értékeinek időpillanataihoz t1, t2, ... tk;
o m parcellákon a koordinátákat yi - t, i = 1, ..., m;
o ábrázoltuk m-dimenziós koordináta-rendszerben.
Nézzük az utóbbi esetben. Az m-dimenziós koordináta-rendszerben minden egyes pont megfelelően létezik bizonyos rendszer állapotát.
A lehetséges állapotok a rendszer Y (y ∈ Y) tekintjük az állapottér (vagy fázistér) a rendszer, és a koordinátáit ebben a térben nevezik a fázis koordinátákat.
A fázis térben minden egyes elemet teljesen meghatározza a rendszer állapotát.
A megfelelő pontban a jelenlegi állapotában a rendszer, az úgynevezett egy fázis, vagy a reprezentatív, pont.
Fázis pályára - egy görbét, amely leírja a fázis pont, amikor az állam a zavartalan rendszer (állandó külső hatások).
Egy sor fázis pályák megfelelő összes lehetséges kezdeti feltételek nevezzük fázis portré.
Fázis portré rögzíti csak az irányt a fázis sebessége a pontot, és ezért tükrözi, csak kvalitatív képet a dinamika.
Építeni, és szemléltesse a fázis portré csak a gépen, hogy van. E. Ha a fázis tér kétdimenziós. Ezért a módszer a fázis tér, amely esetén egy kétdimenziós térben fázis hívják a fázis sík, hatékonyan használják a tanulmány a másodrendű rendszerek.
Fázis koordinátasík a síkra, amelyben a tengelyek a koordináták letétbe bármely két változót (fázis koordináta), egyértelműen meghatározó a rendszer állapotát.
Fix (álló vagy különleges) azok a pontok, amelyek helyzetét a fázis portré nem fog változni az idő múlásával. Különleges feltételek álláspontját tükrözik egyenlő-egyensúlyt.
A szakasz sík azért indokolt, mert a rendszer állapota határozza meg, legalább két változó: az érték a kimeneti koordináta-rendszer és a változás mértéke. A következőkben feltételezzük, hogy az x tengely a fázis síkja a késleltetett kimeneti cheniya ZNA-koordináták y1 = y, és az ordináta tengely - a változás sebessége y2 = y \ „(1. ábra).
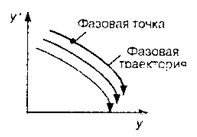
Ábra. 1. példa fázis portré.
Ezután a fázis pályái feszített rendszerben a következő tulajdonságokkal rendelkezik:
o ponton keresztül a fázis sík megy csak egy út;
o felső felében kép pont mozog balról jobbra, és az alján - korom, illetve fordítva;
o at abszcisszán származékot dy2 / dy1 = ∞ mindenütt, kivéve a pontok egyensúly, így a fázis pályagörbék metszik a vízszintes tengelyen (a nem-szinguláris pont) derékszögben.
A lineáris rendszer egyedülálló szinguláris pont - az origó. Nemlineáris B tems jellemzi sokféle fázis portrék - lehet, hogy néhány konkrét kérdésekről.