A szükséges vizsgálati konvergencia
Definíció. Numerikus sorozat egy kifejezés
.
Száma u1; u2, u3; ...; un; ... említett egy számsorozat tagjai és
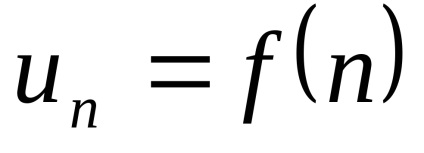
Definíció. A összege az első n elemének a sorozat nevezzük az n-edik részösszegként a sorozatból, és jelöljük Sn. tehát
Különösen: S1 = u1, S2 = u1 + u2, S3 = u1 + U2 + U3 stb A részleges összegeket a számszerű sorrendben formájában
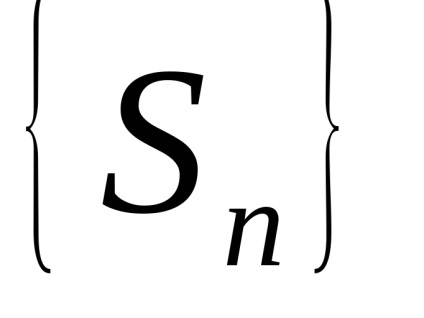
Definíció. A S összege számsor nevezzük határa szekvenciájának részleges összegek
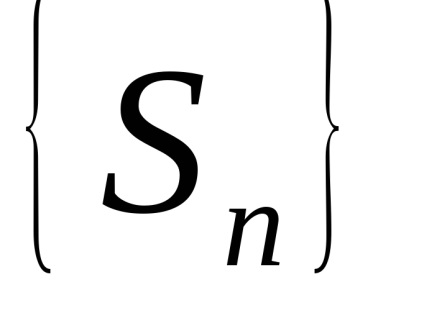
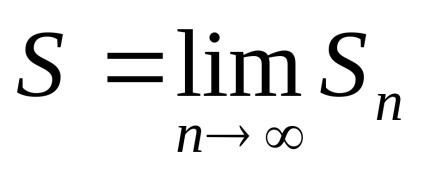
Numerikus sorozat nevezik konvergens. ha azt a mennyiségét (ebben az esetben van egy véges határérték részleges összegeket a szekvencia) és a széttartó. ha ez nem létezik (
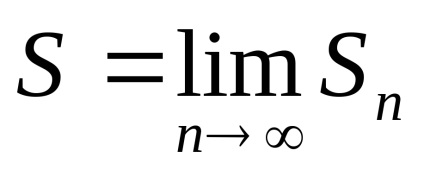
Ha a számsor
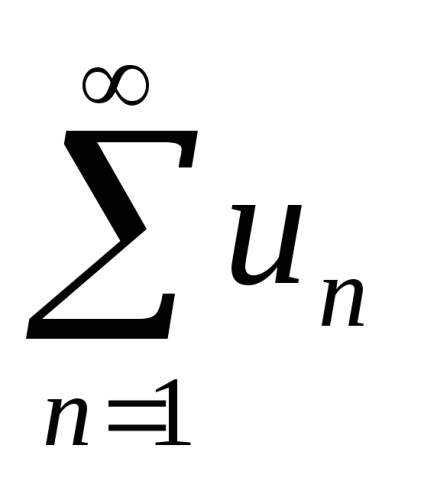
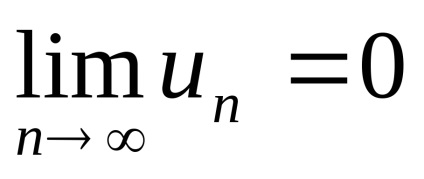
Tekintettel a konvergencia kritériumot kell érteni a következő:
ha
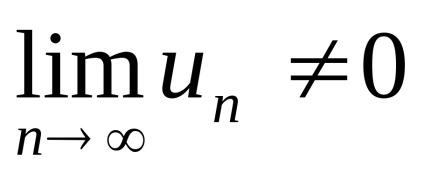
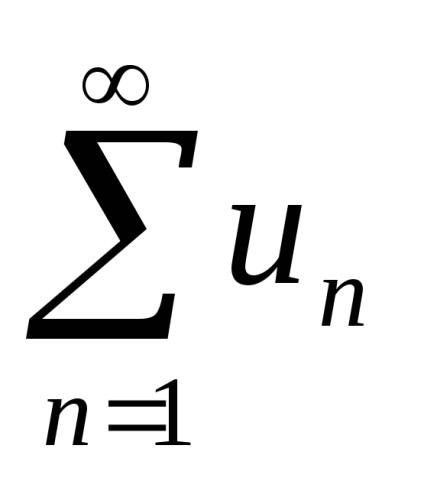
ha
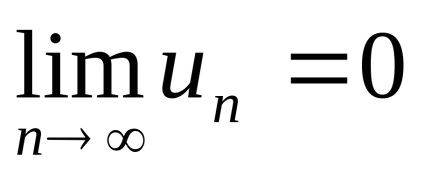
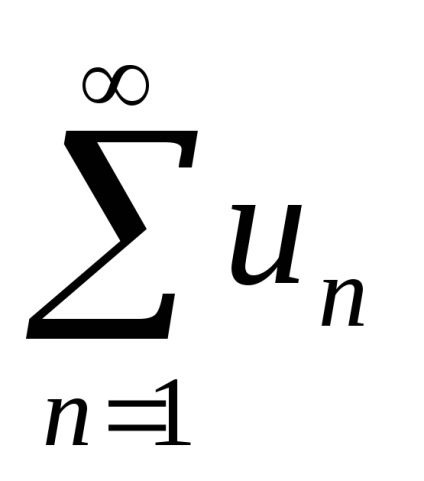
Elegendő jelei egybeesése sorozat
relációs jel 1
Két znakopolozhitelnyh sorozat Tegyük fel, hogy
ahol a tagok száma (1) nem haladja meg a megfelelő tagok száma (2) legalább egyes index n = N. tehát
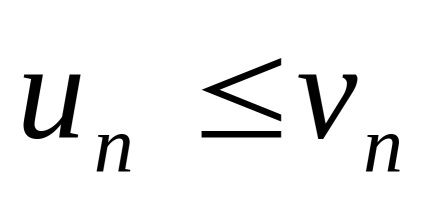
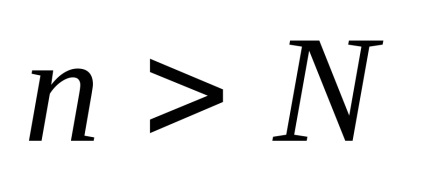
A konvergencia a sorozat (2), és mindig követi a konvergencia a sorozat (1),
Eltérés a sorozat (1) mindig a raskhoimost sorozat (2).
összehasonlítjuk jel 2 (korlátozó)
Ha van egy véges, nem nulla határérték kapcsolatok
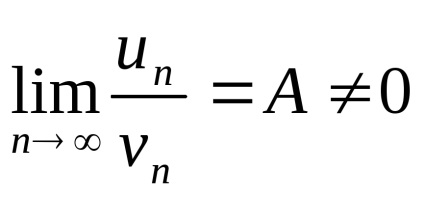
Alkalmazásakor száma szolgáltatásainak összehasonlítása társul egy úgynevezett referencia-sorozat, konvergencia vagy divergencia, amely be van állítva.
referencia-sorozat
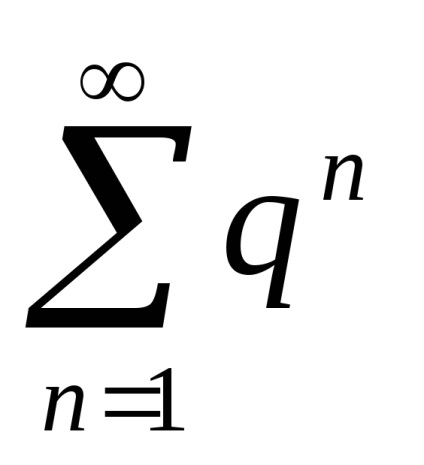
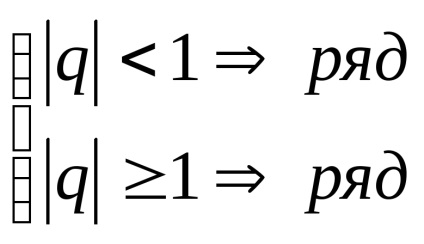
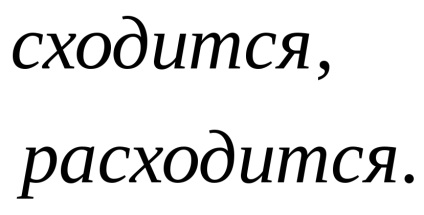
Az általánosított harmonikus sor
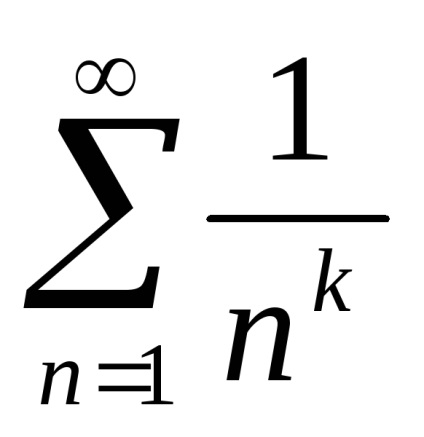
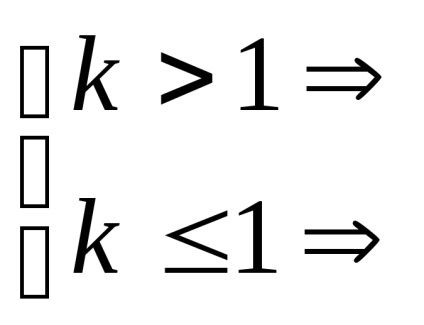
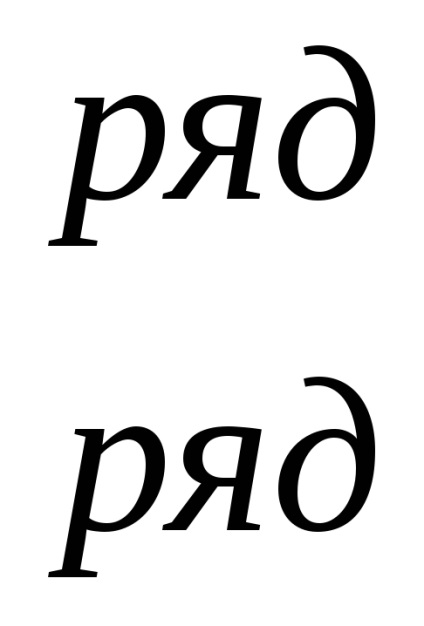
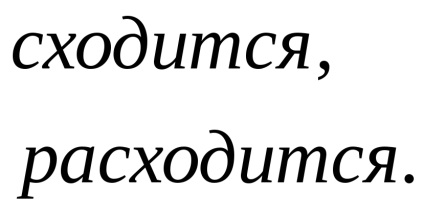
Különösen a k = 1, megkapjuk