A katasztrófák jelei
Tekintsük a katasztrófák jeleit. A katasztrófa létezését a potenciális funkciók családjának speciális kritikus pontjai mutatják ki, amelyek egy rendszert vagy jelenséget írnak le. Az ilyen pontokat azonban gyakran nem ismerik fel azonnal.
Például egy lehetséges függvény nagyon összetett vagy nem pontosan ismert. Még ennél is rosszabb, ha a rendszer nem gradiens, és nagyon rossz, ha nincs egyenletes elgondolás az egyenlet formájáról, akkor megfelel a rendszer által leírtaknak.
A katasztrófák azonban gyakran valós helyzetekben fordulnak elő, ezért fontos időben felismerni őket. A katasztrófák megkülönböztető jellemzői - olyan jelek, amelyek felhívják a figyelmet erre a folyamatra.
Amint egyikük rögzített, azaz a rendszerben lévő katasztrófa jelenlétét jelző jele a rendszer szabályozási paraméterei megváltoztathatók oly módon, hogy megtalálják a fennmaradó jeleket, amelyek szükségszerűen a megfelelő körülmények között találhatók meg. A rendszer leírásában szereplő bizonytalanság esetén a katasztrófa jelenlétének és típusának meghatározása segít meghatározni:
- egy egyszerűsített modell-potenciálfunkció, amely csak a jelentős állapotváltozók és a vezérlő paraméterek függvénye;
- egy potenciális függvény strukturálisan stabil része, amely megmondja, hogy milyen folyamat valósul meg;
- A rendszer egyenletének típusa és annak a módja, ahogyan a potenciális függvény belép;
- szükségtelen az egyenletek általános használata.
A katasztrófák jeleinek leírása
módozat
A rendszer két vagy több különböző állapotot képes megváltoztatni a vezérlő paraméterek valamelyik területén. Például, ha a rendszer vezérlő paraméterei árnyékos területen vannak, akkor a rendszer három különböző állapotban lehet (például az összeszerelési ütközés az 1. ábrán).
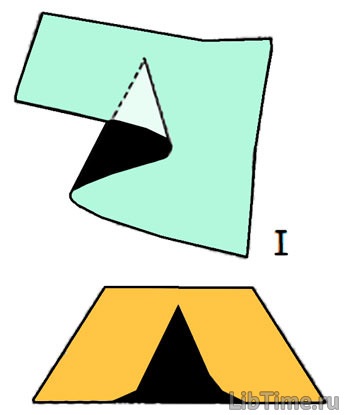
1. ábra - Modalitások és hiányosságok katasztrófa-szerelvényben
megközelíthetetlenség
Van egy olyan terület, amely nem érhető el instabil egyensúlyi állapotokról, amelyek nem érhetők el bármely stabil állapot mentén. Az 1. ábrán. 1 a középső réteg elérhetetlen.
Katasztrofális versenyzés
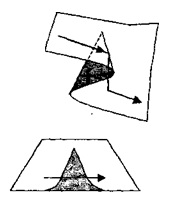
2. ábra - Kataklizma versenyek
Kis változások az értékeket a vezérlő paraméterek okozhat nagy változások az értékek az állapotváltozók, mint, hogy a rendszer a rendszer ugrik egy helyi minimum, hogy egy másik, az átmenetet a környéken egy helyi minimum, hogy a másik egy nagy változás értékeit állapotváltozás fordul elő, hogy az ultra-gyors léptékű .
Az 1. ábrán. 2 az ugrás akkor következik be, amikor a rendszer állapota a szerelvény katasztrófafelületének egyik rétegétől a másikig áthalad.
különbség
Az ellenőrző paraméterek végső változásai az egyensúlyi ponton az állapotváltozók értékeinek végső változását eredményezik.
Általában a vezérlő paraméterek kezdeti értékeiben bekövetkező kisebb változások csak az állapotváltozók kezdeti és végső értékeinek enyhe változását eredményezik. Katasztrófa jelenlétében azonban az állami változók kezdeti értékeiben bekövetkező kisebb változások nagy változásokhoz vezethetnek e változók végső értékeiben.
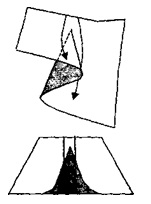
3. ábra - Különbség
Az 1. ábrán. A 3. ábra azt mutatja, hogy a szabályozó paraméterek változásának pályája a rendszer szoros kezdeti állapotához képest jelentős különbséget eredményez a rendszer végállapota között.
Hiszterézis és visszafordíthatatlanság
Hiszterézis akkor következik be, amikor a folyamat nem teljesen reverzibilis. Ugrás egy helyi minimum 1 egy helyi minimum 2 nem kerülhet sor az azonos értékeket a kontroll változók, bár a folytatásban a 2. pont 1. pont alatt került sor mozgás az ellenkező irányba.
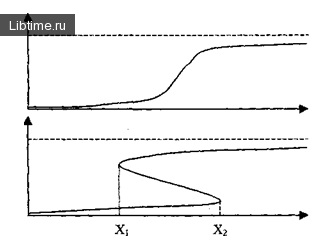
4. ábra - hiszterézis jelenség
Tekintsük a munka hatékonyságának és a javadalmazás függőségét. amelyért dolgozik. A javadalmazás növekedésével a munkaerő hatékonysága is növekedni fog. Ha a jutalom nem elegendő, akkor a munkavállaló nagyon próbálkozik. Másrészről, mindenkinek van hatékonysága, és bármi legyen is a jutalom emelése, nem lesz nagyobb hatás elérése.
Ezt a helyzetet megközelítőleg az 1. ábrán bemutatott függvény írja le. 4.
Tekintsünk most egy dinamikus folyamatot, amelyben a fizetés növekedhet és csökkenhet. Ha a kezdeti kifizetés alacsony, akkor a munka hatékonysága is alacsony. A kifizetések növekedésével a hatékonyság növekszik, de lassan, mert a munkavállaló szerint a fizetésemelés nem elegendő a munka hatékonyságának növeléséhez.
Ez addig fog megtörténni, amíg X2 pillanat, amikor a fizetés további növekedése átmenet egy minőségi új teljesítményre. A hatékonyság hirtelen megváltozik.
Ha éppen ellenkezőleg, a kezdeti időpontban a fizetés magas, akkor a hatékonyság magas szinten marad. A fizetéscsökkentés során fokozatosan csökken a hatékonyság (csökken a tehetetlenség, amely szerint a személy szokásos módon dolgozik).
Ez akkor történik, ha a kifizetés eléri az X1 meglehetősen alacsony szintjét. Ezen a ponton a hatékonyság jelentősen csökken, hiszen nincs ösztönző magas szinten tartani. A 3. ábrán látható ábra. 4b, a hiszterézis huroknak nevezzük.
Szigorúan véve, ez nem egy függvény, mivel ugyanazt az értéket X megfelelhet két (vagy akár három) értéket W. A jelenléte több ilyen X - [Xp X2], és ahhoz a lehetőséghez vezet katasztrofális változások a rendszer állapota. Az [Xt; X2] egy bifurkációs készletnek nevezzük. azaz ilyenek azok a paraméterek értékei, amelyekből a rendszer több különböző állapota lehetséges. Az 1. ábrán. Az 5. ábra ugyanazt a jelenséget mutatja egy háromdimenziós rendszerben.
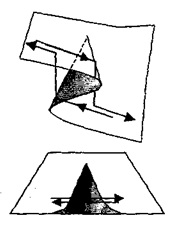
5. ábra - Irreverzibilitás egy háromdimenziós rendszerben
Tehát egy katasztrófa éles, hirtelen változás a rendszer állapotában, lassan változik a paramétereiben (vagy a kontrollváltozókban).
Visszatérve a példa, akkor észrevehetjük, hogy amikor forgatni a tengelyt, és megvizsgálja a fizetési függvényében a hatékonyság, van dolgunk a harmadik fokú polinom (4.). Ennek a polinomnak nincs extrema, és a 3. ábrán. A 4b két szélsőséges. Nyilvánvaló, hogy a szélső pontok száma függ a polinom együtthatóitól, azaz a polinomok számától. rendszerparaméterek.
Tekintsük a lehetséges funkciók helyi jellegét. Az egyensúlyi állapotok tulajdonságai függenek a potenciális függvény típusától és tulajdonságaitól, amely leírja a rendszer viselkedését. Korábban az egyensúlyi állapotok kétdimenziós rendszerekben történő osztályozását tekintették, ahol nyolc különböző egyensúlyi változat lehetséges. Ha a rendszer állapotváltozói nagyobbak, akkor az egyensúlyi állapotok teljes besorolása igen nehéz.
A katasztrófák elmélete lehetővé teszi egy ilyen osztályozás elvégzését a nemlineáris rendszerek meglehetősen széles osztályára.
Vizsgáljuk meg, milyen lehetséges átalakítások lehetségesek az egyensúlyi állapot szomszédságában. Ezek az átalakítások lehetővé teszik a funkció egyszerűsítését és helyben egyszerű formába juttatását, és kiemelik a katasztrófákat.
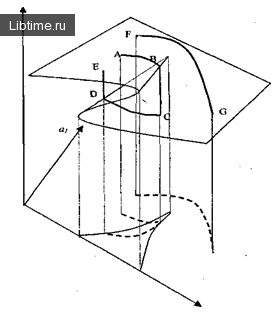
6. ábra - A szerelvény balesete
Amint az ábrából látható, a rendszer megkezdi annak mozgását a pont, ameddig lehet mozgatni a tetején a felület, amíg el nem éri a beállított szingularitás B pontban Ezután a rendszer végez egy éles ugrás le a C pontot és aljára kerül a felszínre.
Ha a rendszer elindítja a mozgását az alján, akkor átmegy a D pontban levő kettős elágazáson, és éles ugrással a felsõ felületre. A rendszer másik viselkedése lehetséges, amely nem tartalmaz éles átmenetet. Például az FG útvonal mentén, ha a rendszer egyik paramétere is gyorsan változik.
A katasztrófák elméletének gazdasági alkalmazása nagymértékben a geometriai vonatkozásokra támaszkodik, elsősorban a gazdasági viselkedés leírására, pontosan a gyülekezés katasztrófájára. Más elemi katasztrófákat nehéz megmutatni, mert egy vagy több paraméter megszilárdítását igényli.
A katasztrófaelmélet számos problémát vizsgál, beleértve a tőzsdék összeomlását, a kormányzati viselkedést, a makromodelleket, a Walras feltételezésének szerkezeti aspektusait stb.