A kartográfiai előrejelzések torzulása - stadopedia
A kartográfiai előrejelzések fogalma
A kartográfiai vetület egy földi ellipszoid felületének matematikailag meghatározott leképezése egy síkban. Ebben az esetben a leképezett objektumok pozíciói és körvonalai átkerülnek a térképre, valamint a meridiánok és párhuzamok rácsára. A kartográfiai vetületet meghatározó törvény kifejezhető:
1. egyenlete;
2. A grafikus felépítés feltüntetése;
3. A koordináták és egyéb módszerek táblázata.
A térképészeti vetület egyenlete két egyenlet, amely meghatározza a térképen lévő pontok koordinátáinak és az ellipszoid felszínének megfelelő pontjai közötti összefüggést.
A koordinátarendszerek kartográfiai, téglalap alakú, kilométeres és egyéb rácsok. Kartográfiai rács - van párhuzam és meridián kép a térképen.
A térképről egy téglalap alakú rács koordinátarendszer egy sík négyszög koordináták rendszerében egy adott térképprojektben.
Egy kilométeres rács egy koordináta-rács, amelynek vonalai a térképen rajzolnak bizonyos számú kilométeres időközönként. A térképen lévő rácsvonalak metszéspontjait csomópontoknak nevezik.
A térképet a hosszúságok, négyzetek, szögek és alakzatok torzításával jellemzik.
1. A hosszirányú torzításokat abban a tényben fejezik ki, hogy a térképen lévő hosszméret változik az egyik pontról a másikra való áttérés esetén, és egy adott ponton az irányváltás is;
2. A területek torzulása abból fakad, hogy a tér különböző területein lévő területek mértéke eltérő;
3. A sarok torzulások abból állnak, hogy a térképen lévő irányok közötti szögek nem egyenlők a földfelszín megfelelő sarkaival. A földrajzi objektumok vonalai közötti szögek torzulnak, ami maguk a tárgyak formáinak megsértéséhez vezet;
4. A formák torzulása abból a tényből áll, hogy a térképen lévő objektumok ábrái nem hasonlítanak a terepen található megfelelő földrajzi adatokhoz.
A térképen mindenféle torzítás egymáshoz kapcsolódik, és ezek megváltoztatása a többi változást jelenti. A területek és a szögek torzulása közötti kapcsolatnak különleges szerepe van. Az egyikben bekövetkező csökkenés a másikban történő növekedést eredményez. Nincsenek torzítás nélküli térképek, de vannak olyan térképek is, amelyekben sem a sarkok torzulása, sem a területek torzulása, vagy a sarkok és a négyzetek torzulása kiegyensúlyozott.
A hosszirányú torzítások indexe egy adott pontban ebben az irányban egy adott μ hosszméret, amelyet a fő skála frakcióiban fejezünk ki. Ez nagyobb lehet, mint a fő (például: 2.32), és kisebb is, mint például (0.81). A μ skála egy adott ponton változtatja az értékét az iránytól függően. Egy adott pont egyik irányában a hosszméret a legnagyobb, másrészt a legkisebb érték. Ezek az irányok egymással merőlegesek, és ezeket a fő irányvonalaknak nevezik. A legnagyobb méretarányt jelöli, és a legkisebb - A meridiánok mentén lévő hosszméreteket - és a párhuzamok mentén - különösen megkülönböztetik (2.1. Ábra). Néha a hosszúság torzításának indikátoraként nem a skálák értékeit és azok egységességi különbségeit vesszük figyelembe, vagyis ezt a mutatót viszonylagos torzításnak nevezzük, és gyakran százalékosan fejezzük ki. Bizonyos esetekben a hosszúság torzulásait egy bizonyos hosszúságméret logaritmusával becsülik meg, például ha egy adott ponton nincs torzítás, azaz
A területi torzulások mutatói a területek főbb léptékében kifejezett területek egy bizonyos mértékét jelzik. Egy vagy több is lehet. Ehelyett a relatív mutatót gyakran százalékban fejezik ki, és
Ábra. 2.1. Elsődleges szférikus háromszög
A szög egy adott pontján a szög torzításának mértéke a szög oldalainak irányától függ. Ezért a térképen lévő sarkok torzulásának jelzőjeként a legnagyobb torzítást elfogadjuk, a térkép adott pontján a szögek legkisebb torzulása mindig nulla. A térkép bármely pontján mindig van olyan szög, amely torzítás nélkül jelenik meg. Ez a szög a fő irányok között, ami mindig 90 °. Ezenkívül a meridiánvonalak és a párhuzamok vonalán lévő képek közötti szög jellemzőjének jelzőjét alkalmazzuk. Ez a szög a térképen általában nem egyenlő a szög közötti hosszúsági és párhuzamos és jelöljük (théta), és annak eltérés a szög értékének közötti hosszúsági és párhuzamos a referencia felület, amely jellemzi a torzítás, - (epszilon). A forradalom golyóján vagy ellipszájában a meridiánok és a párhuzamok merőlegesen metszik egymást. Ezért a jelzett
A formák torzulása (valamint a szögek) annak a ténynek a következménye, hogy a különböző irányú hosszúságok eltérőek. Ezért az arány a formák torzulását jellemzi. Minél nagyobb az érték, annál erősebb a kiterjesztés a kontúr irányában a térképen. A K exponens a végtelen számok formáinak torzulását jellemzi. A véges számok esetében ez közelítő mutató. Tökéletesen tükrözi a viszonylag kis földrajzi tárgyak, például a Krím-félsziget, a Tasmania-sziget és a Kola-félsziget formáinak torzulását. De a nagy tárgyakhoz, például a kontinensekhez és Grönland szigetéhez hasonlóan, pontatlan. Más mutatókat használnak, például:
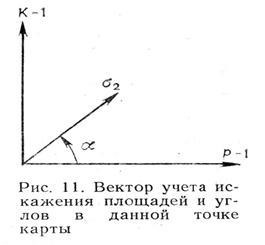
A mutató figyelembe veszi a területek torzulását és a formák (szögek) torzulását. Ha a koordinátarendszer vektoraként tekintjük (11. ábra), akkor a vektor forgatását meghatározó szög a következőképpen számítható:
A területek arányát és a szögek torzulását jellemzi.
Ha nincsenek torzulások a sarkoknál, a torzulások hiányában azokon a területeken, ahol az alakzatok és a területek eltorzulnak, kiegyenlítettek, azaz
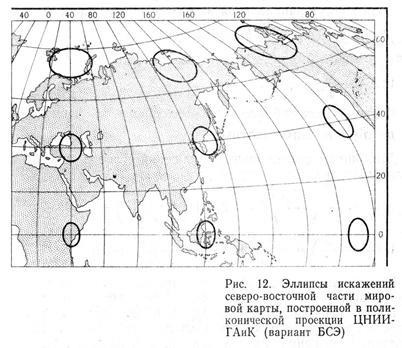
Pontosabban, a térkép adott pontján mindenféle torzulás a torzítás ellipszisaként jeleníthető meg (12. és 13. ábra). A térkép adott pontján a torzulások ellipszise a relativitás felszínén egy infinitezimális kört képvisel. A félpólusai megegyeznek a nagyságrendekkel, és a fő irányban vannak orientálva. A torzító ellipszis vektor sugara bármely irányba orientálható, és meghatározza a hosszúságok gyakori skáláját ezen irányba. Az ellipszis alakja a szögek és alakzatok torzulását jellemzi - ezek torzulnak, annál inkább az ellipszis különbözik a körtől. Az ellipszis területe arányos a terület torzításával, és annál inkább, annál torzabb a terület. Ha torzulások ellipszisét szeretné ellensúlyozni a térképen, feltétlenül vegyen végtelen értékű (például 5 mm méretarányú) golyóval vagy ellipszoiddal a végtelen körök sugarait. Ezután a térképen megjelenő összes ellipszis véges értéket is tartalmaz.
Összehasonlíthatóak és összehasonlíthatók a térképen bemutatott adatokkal, ahol nincs torzítás vagy a torzítás egyik típusa hiányzik. A torzítások nagysága és jellege, amelyet minden ellipszis igazol, a térképnek az ellipszis középpontjába kell kerülnie.
A térkép meghatározásával vagy a meridiánok és párhuzamok mentén lévő hosszúságok részleges skálájának kiszámításával és a köztük levő szöggel könnyen kiszámítható a torzítás ellipszis paraméterei (13. ábra). A torzítás ellipszis és (a forradás golyó vagy ellipszo) féltengelyeit a következő képletek találják:
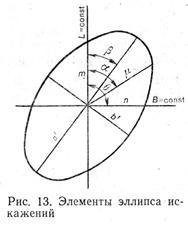
Az ellipszis fő tengelyének térképén azimutot az alábbi képlet adja meg:
Tudva, hogy a térkép egy adott pontján könnyű elrendezni a torzítás ellipszist. Ezekből az adatokból könnyű megtalálni a torzítás egyéb mutatóit. A térképen azimut által meghatározott tetszőleges irányú hosszúságok egy adott skála az alábbi képlet alapján található:
A térképen a torzítás értékek megváltoznak. Egyes kartográfiai vetületekben vannak olyan központi pontok vagy vonalak, amelyekben a torzítások (általában a sarkok) kicsiek, és a távolságtól kezdve lassan először, majd gyorsabban nőnek. E növekedés mértéke eltérő irányban eltérő lehet. Általában a térképeken vannak olyan pontok vagy vonalak, amelyekben az egyéni vagy mindenféle torzítás hiányzik. Ezek zérus torzítású pontok és vonalak. A maximális torzítással rendelkező helyek általában a legtávolabb vannak a vonalaktól vagy a zéró torzulástól. Annak érdekében, hogy a maximális torzítás a lehető legkisebb legyen, a térkép középpontjában egy zérus torzítású pont vagy vonal található. Ha a vonal bezáródik, vagy két vonal van, akkor úgy helyezkednek el, hogy a távolság azoktól középre és a térkép élei megközelítőleg azonosak legyenek. A torzítások a központi vagy nulla torzítású pontokból vagy vonalakból történő elmozduláskor megváltoztak, célszerű az izokolok megjelenítését.
Az Isokoly olyan vonalak, amelyek egy vagy több torzítási index azonos értékű pontokat kapcsolnak össze. Ikonok láthatóak a makett kártyákon. Általában néhány atlaszban, valamint a matematikai térképészet kézikönyvében, az izokolokkal és
A torzítási értékek megjelenítésének másik módja az, hogy összeállítanak táblákat egy bizonyos torzítási mutatóval.
A fentiekben helyi mutatókat tartottunk számon. Ezek jellemzik a torzításokat a térkép pontján. Néha a torzításokat a vetületek különböző változatainak összehasonlítása érdekében a torzító mutatók használatával használhatja, amelyek a térkép egészét jellemzik. A variációs típus indexe használatos:
ahol az ábrázolt terület területe az egyik mutató. Gyakran az integrált értéket egy összeggel helyettesítik, amelyre a képterület szelvényekre oszlik, az egyes szakaszok területét a torzítási index képezi, és a következő képlet segítségével számítható ki: