Itcs - népszerű
Ma egy ilyen kezdetben látszólag triviális dologról beszélünk válogatásként. Nagyon gyakran láthatjuk, hogy megtanulják és tanítják, valamint a rekurzió témája, azaz gyakorlatilag nem tanítanak és nem tanítanak :). És a "teáskannák" című könyveknél és általában a legtöbb könyvben ez a kérdés nem kap semmilyen figyelmet, mert minden, ami a gyors hatásra irányul.
Érdekes dologról van szó, az emberek összetett adatbázis-struktúrákat gyűjthetnek, multithreading-et használnak, és így tovább. de a rendezés, a sorok, a halomok, az adatrészletek kezelése valami arhizom. Sokan vitatják a fentieket, de kérdezhetem, láttad, hogy a válogatás a program lefagyásakor használatos? Például a rosszul fejlett fejlesztések keretében nem ritka. Mindenki hozzászokott a magas szintű modellekhez, és egyes esetekben az emberek előkészített módszereket használnak, bár belső felépítését nehéz elképzelni. Eközben ismerni kell a válogatási elveket, különösen az AI programozóit.
Általában az élet érdekes dolgokat mutat. A 90-es évek közepén, amikor megbízásokat hajtottam végre, adatbázisokat tároltam szöveges fájlokban (szimbólumhatárolókkal vagy anélkül), és ennek a struktúrának a kezelése egy adott nyelv funkciói miatt valósult meg. Aztán röviden átnéztem a HTML-t, és úgy döntöttem, hogy a html-címkék nagyon kényelmesek, mint karakter-határolók. És csak néhány év alatt létezett olyan szabvány, mint az XML. Vagyis a gondolatok konvergáltak, és kiderül, hogy egyszerre fejlesztettem ki és használtam a jövő technológiáját. Most tárolok adatbázisokat a végrehajtható Lua-fájlokban, amelyek nemcsak az adatokat tartalmazzák, hanem a számukra alkalmazható összes módszert, valamint az egymással összefüggő struktúrákat. Tartalma dinamikusan változhat.
Saját adatbázis-struktúrájának létrehozása és egy igazgatási rendszer megvalósítása egyáltalán nem nehéz, de a számítógép-használók megszokták, hogy sok időt töltsenek készen a technológiák tanulmányozásával és felhasználásával.
Beszéljünk a válogatásról. Számos algoritmikus modellt fejlesztettek ki, vagyis a témát alaposan tanulmányozták, de érdemes megemlíteni azt a pillanatot, amikor meg kell ismernie az alapelveket, és minden egyes esetben ugyanazt a válogatást kezelheti.
A válogatási kérdések megoldása előtt ismernie kell a feldolgozni kívánt adatok mennyiségét. Vannak olyan módszerek, amelyek a leghatékonyabbak egy csekély elemszámmal, de nagyokká válnak, amikor nagyok. Vannak speciális módszerek is, amelyek közül az egyiket az anyag végén vizsgáljuk.
Egy egyszerű módszer - buborék válogatás
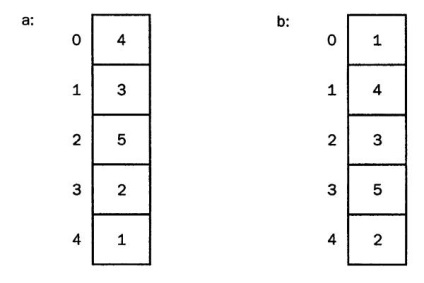
Buborék válogatás. a az eredeti tömb; b - a negyedik elem "lebeg" a felszínre.
Ennek a módszernek a neve leíró, vagyis a víz felszínén lebegő levegő buborék. Elvileg ez egy jó és érthető összehasonlítás.
Képzeljen el egy egész számot, amely például öt elemből áll. Meg kell rendezni őket a növekvő sorrendben a számok, azaz az adatok [0] tartalmazza a minimális számot, és az adatok [4] a rendelkezésre álló maximális. Mi történik ezen algoritmus keretében? Kezdetben a legmagasabb elemadatokat [4] hasonlítjuk össze az előző adatokkal [3], és ha az értéke kisebb, akkor az elemek egymással kicserélődnek. És így tovább, amíg a minimális elem felbukkan, mint egy levegőbuborék. Tény, hogy mindaz, amit elmondtak, könnyebben leírható lesz a kóddal:
ha (tömb [i-1]> tömb [j]) swap (tömb, i-1, j);
a méret a tömb méretét jelenti, de a hurokon belül az 1-es értéket veszi fel, mivel a maximális elem automatikusan elfoglalja pozícióját. A hurok belsője ellentétes irányba halad a külső irányhoz képest, bár előrefelé is megtehető.
A buborék válogatásának módszere egy hátránnyal jár - számos tevékenység, vagyis erőforrás-igényes. Ugyanakkor, miután elemeztük, megmondhatjuk, mi a fő probléma - az elemek mozgása egy helyen.
Egy egyszerű módszer a szelektív válogatás
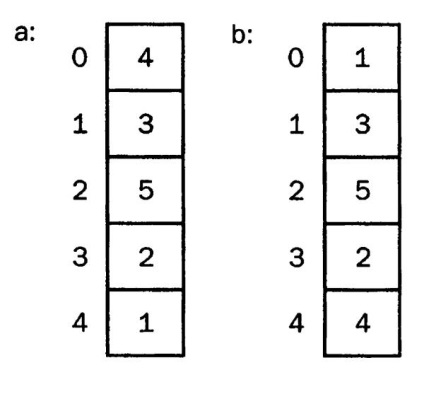
Egyedi válogatás. Ez azt mutatja, hogy a tömb utolsó eleme hogyan változik az első helyével.
Lehetséges-e az elem összevetése az összes rendelkezésre álló eszközzel, és ha a feltételek teljesülnek, akkor a pozícióadatok [0] leszek, így csak egy csere van? Igen, ez a szelektív válogatás. A buborék egy továbbfejlesztett verziója. Vagyis kezdetben a minimális érték megtalálható az egész tömbben, indexe meghatározva. Ezután az adatok [0] és az adatok [a minimális érték index] swap. Ezután a következő alréteg kerül felvételre, amelyben az [0] adatot nem veszik figyelembe, és az adat minimális értékével [1] stb. Töltjük ki.
A kódban ez egy kicsit terjedelmes (ezért az informatikai médiumok gyakran szidják :)), ezért mondjuk, hogy egy belső hurokra van szükségünk, amelyben megtaláljuk a minimális számot tartalmazó elem indexének értékét, majd végezzünk egy permutációt. Ezután ugyanazt a keresést végezzük a részhalmazban, és így tovább, ami a külső hurokban történik. Ebben az esetben a kódot úgy optimalizálják, hogy a permutacionális elem nem tartalmazza a minimális értéket, azaz ha (min_index! = I), akkor a permutációra korlátozódik.
Komplex módszer - gyors válogatás
A gyors szortírozás az egyik leghatékonyabb módszer, és lényegében ezek egymással összefüggőek. A módszer abban áll, hogy a tömb a választott bármely elem, hogy fog működni, mint egy elválasztó értéket. Eltávolítás (!) - ez azt jelenti, hogy el fog különülni. És pontosan mi? Valójában, ez úgy értendő, kétirányú forgalom elejétől a tömb és annak végén, a terminológia könnyebb használni a nevét Head (fej), és Tail féle (farok). Vagyis, ha beszélünk az egyensúlyt a számokat növekvő sorrendben, a rendezési algoritmus a fej lesz összehasonlítani a számokat a feltétel> értéket osztani (ha „igen”, akkor ez egy nagy érték változások megosztás), és a rendezési algoritmus Tail lesz összehasonlítani a szám a feltétel <разделяющего значения (если «да», то это большое значение меняется с разделяющим). В момент когда Head и Tail сходится на одном элементе (место пересечения указателей), мы можем сказать, что все что справа (или ниже) меньше разделяющего значения, а все, что слева(сверху) — больше.
Ez a két rész ugyanúgy rendeződik külön-külön (a rendezési funkció rekurzívan nevezi magát).
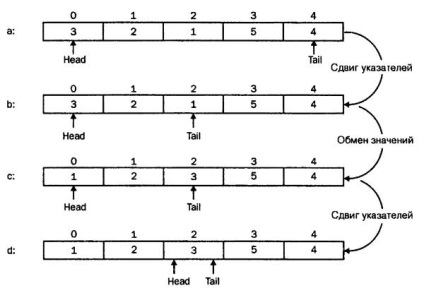
Gyors válogatás. Az elválasztó értékként 3 (bal szélső érték) van kiválasztva. Tail, elérve egy egységet (b) találkozik az "aktuális érték" állapotával <разделяющего», Происходит обмен. Потом идет проверка со стороны Head, так как ситуация изменилась, указатели пересекаются на элементе массива a[2]. Следующим этапом будет идентичная обработка правой и левой частей.
A gyors algoritmust gyakran a "megosztás és meghódítás" kifejezés kísérte. Ez így van, de nagymértékben függ az elválasztó elem / érték kiválasztásától. Például egy, a -3,5,0,7,2-t tartalmazó tömböt. Próbálja választani az értéket, amely biztosítja a leggyorsabb rendezési (legkényelmesebb az egyik az első válogatás ciklus lesz 0 vagy 2), és a leglassabb (amikor az első válogatás ciklus kiválasztása elválasztó maximális vagy minimális érték, azaz -3 vagy 7 ). A legelőnyösebb helyzet akkor is, ha a tömb két egyenlő részre oszlik.
Továbbá, ha alaposan megnézzük, akkor azt találjuk, hogy egyes esetekben a gyors válogatás nem nyer, mint az általunk írt egyszerű módszerekhez képest. És a legnagyobb hátránya, hogy gyors rendezést alkalmazunk egy már rendezett tömbre.
Általánosságban több módja van a gyors válogatásnak, fő különbségük az elválasztási érték (a partícionálási eljárás) kiválasztásának algoritmusa, a rekurzió optimalizálása.
A gyors válogatásnak még egy vidám mínuszja van - belépett a végtelenbe. Ez azt jelenti, hogy a 3,2,3-os tömb kritikus helyzethez vezet, mivel az ismétlõdõ értékek feldolgozásának eljárása szükséges, ami nem szerepel a standard algoritmusokban.
Egy kifinomult módszer javítja a gyors válogatást
A gyorsabb válogatás jobban illeszkedik az elválasztási érték kiválasztásához. Meg kell határozni a tömb mediánját, vagyis a középértéket a teljes spektrumban. Definíciója meglehetősen költséges, de annál több értéket kell feldolgozni, annál jobb az erőforrások egyensúlya.
A medián meghatározásához rendszerint átlagérték van a két szélső és középső elem között. A helyzet ismételt értékekkel történő megoldásához speciális eljárás van, amely a (...<=… или …>= ...), vagy egyszerűen kiegyenlítették a helyzetet egyenlőség esetén.
Összetett módszer a merge sorting
egyesíti magában válogatás válogatás funkció particionálni a tömb felét - két almátrixszá válogatás után függvény saját magát hívja rekurzívan az egyes felét, majd egyesíti a rendezett almátrixszá egyetlen tömbben. Minden rendezési munkát végezni kell, mivel a hívások halmaza le van húzva. Ez működéséhez szükséges az algoritmus további közbenső tömb azonos méretű, mint az eredeti, amelyet másolni a fő üzenet.
Az egyesítéssel történő rendezés jobb, mint a gyorsabb válogatás, mivel az egyszerűség (nincsenek elválasztó elemek és a mutatók áthaladása), és nincs a legrosszabb esetben a gyors rendezés során előforduló probléma.
Egy kifinomult módszer a "diszkrét rendezés"
Az emlékezetemben csak néhányszor találkoztam vele. Nekem azonban szüksége volt rám, ezért saját magam fejlesztettem ki. Lényegében ez az algoritmus úgy működik, mint az ADC és számos más jól ismert algoritmus. Ez azt jelenti, hogy kezdetben a maximális és a minimális értékeket keresik a tömbben. Ezután kiszámítják az átlagukat, azaz a / 2 értékek tartományát. Ezután minden elem átmegy ezzel az értékkel, és a kisebbek hozzáadásra kerülnek a bal oldalon, a nagyobbak - a jobb oldalon. Ez létrehoz egy ideiglenes tömböt az azonos méretű, mint az eredeti, amelyben az elemek kerülnek a bal oldalon az indexek, a semmiből, és az, hogy nem maradt - az [az összes e-nek - a jelenlegi index a jobb oldalon].
Ezután (mindegyik fél esetében már ismerjük az átlag 1/4-es értékét, az értéktartomány 3/4-ét, valamint az egyes elemek számát), összehasonlítjuk a felek átlagértékét is, és így tovább, amíg el nem éri egy elem. Ezután egy összeállítás van a mutatók megfelelő elrendezésével. A "diszkrét rendezés" és az egyesítés szétválogatásához egy további tömb jelenléte szükséges, vagyis azt mondják, hogy nem történik "helyben".
Nem azt kell mondanom, hogy a diszkrét rendezés algoritmusa fáradságos a végrehajtásban, bár a végrehajtás összetett változata is létezik. Ő megbízható, de elég erőforrás. Rendkívül alkalmas heterogén tömbök esetében, ahol "üregek" vannak, azaz például 0 és 100 közötti tartományok, és az elemek értékeinek nagy része a 80-90 tartományban koncentrálódik. Általában a diszkrét rendezés fő vonzereje és módszerei olyan esetekben nyilvánulnak meg, amikor kerek értékeket, a dinamikusan feltöltött tömbök bizonyos részeit nyomon kell követni, és így tovább.
Mint látható, semmi különös nem volt feltalálva a válogatási folyamatban. Csak alaposan meg kell néznie. Maguk az algoritmusok nagyon jól megkönnyítik azokat a körülményeket, amikor jól ismerik a probléma belső szerkezetét. Például ha az általános esetben ez vagy az algoritmus erőforrásigényesnek és hibaként eldobható, akkor magánjellegűen a leghatékonyabb a korlátok helyes elrendezése.
Az anyag következő részében beszélünk a veremről és rekurzióról, a rekurzió optimalizálásáról.