A harmonikus linearizáció ötlete
Nemlineáris rendszert tartunk szem előtt, amelynek a rendszere a 12.2a. A rendszer Wl (s) átviteli függvényből álló lineáris részből és egy NL specifikusan meghatározott jellemzővel rendelkező nemlineáris összeköttetésből áll. A -1-es együtthatóval rendelkező kapcsolat azt jelzi, hogy a rendszer visszajelzése negatív. Feltételezzük, hogy vannak olyan auto-oszcillációk a rendszerben, aminek a mértékét és gyakoriságát szeretnénk megtalálni. Ebben a módban a nem lineáris kapcsolat X bemeneti változója és az Y kimenet időbeli időfüggvények.
A harmonikus linearizáció módszere azon a feltételezésen alapul, hogy a nemlineáris egység bemenetén a rezgések szinuszosak, e
ahol A az amplitúdó, és ezeknek az öngenerált oszcillációknak a gyakorisága. a az esetleges állandó komponens az általános esetben, amikor az ön-oszcilláció aszimmetrikus.
Valójában a nemlineáris rendszerek ön-oszcillációi nem szinuszosak, mivel formájuk torzulása nemlineáris kapcsolattal történik. Emiatt, a fenti kiinduló feltevést ÓZNA-chaet, hogy a módszer harmonikus ?? lin earizatsii alapvetően hozzávetőleges, és annak alkalmazási területe olyan esetekre korlátozódik, amikor a rezgések bemeneti Neli-lineáris-link elegendően közel szinuszos. Annak érdekében, hogy ez megtörténjen, a rendszer lineáris része nem lépheti túl az öncsillapítások magasabb harmonikáját, azaz alacsonyabb átszűrőnek kell lennie. Ez utóbbit az 1. ábrán mutatjuk be. 12.2, b. Abban az esetben, amikor például az ön-oszcilláció frekvenciája egyenlő, a 3. ábrán látható lineáris rész. 12.2, b AFC fog működni, mint egy aluláteresztő szűrőt ezek a rezgések, mint a második harmonikus, amelynek frekvenciája megegyezik a 2, gyakorlatilag nem adja át a bemeneti NONLIN ?? eynogo linkre. Következésképpen ebben az esetben a harmonikus linearizálás módszere alkalmazható.
Ha az ön-oszcillációk frekvenciája egyenlő, a lineáris rész szabadon áthalad a második, a harmadik és az egyéb önmegoszlások harmonikusán. Ebben az esetben nem lehet azt állítani, hogy a nemlineáris egység bemeneteinek oszcillációja elég közel lesz a szinuszos, ᴛ.ᴇ értékhez. Az előfeltétel nem teljesül a harmonikus linearizációs módszer alkalmazásához.
Annak megállapításához, hogy a rendszer nyelvi része aluláteresztő szűrő, és ezáltal meghatározza a harmonikus linearizáció módszerének alkalmazhatóságát, rendkívül fontos tudni az automatikus oszcillációk gyakoriságát. Ugyanakkor csak a módszer használatával lehet felismerni. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, a harmonikus linearizációs módszer kiválasztását már a vizsgálat végén az ellenőrzés sorrendjében kell meghatározni.
Itt jegyezzük meg, hogy ha a vizsgálat eredménye, hypo-tézis, hogy Lin ?? eynaya rendszerének részét szűrőként viselkedik LO-frekvencia nem erősítették meg, de még mindig nem jelenti azt, hűtlenség eredményeket, bár természetesen, teszi őket som és további ellenőrzést igényel más módszerrel.
Tehát feltételezve, hogy a rendszer lineáris része egy aluláteresztő szűrő, akkor azt feltételezzük, hogy a nem-lineáris kapcsolat bemenetén lévő öngenerált oszcillációk szinuszosak, vagyis a formában (12.1) vannak. A kapcsolat kimenetén a rezgések nem szinuszosak, mivel a nemlinearitás torzítja őket. Példaként, 12.3 A bemenet tiszta szinuszos jelének meghatározott amplitúdójára a nemlineáris kapcsoló kimenetén egy görbét ábrázolunk az azonos szakaszban megadott kapcsolat jellegéből.
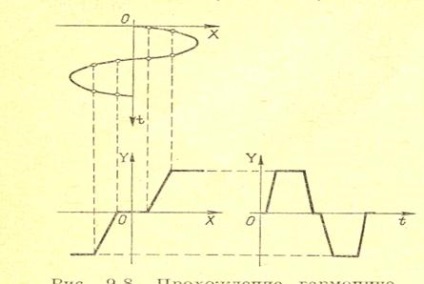
Ris.12.3. Egy harmonikus oszcilláció átadása nemlineáris kapcsolaton keresztül.
Ebben az esetben, hiszen úgy véljük, hogy a rendszer lineáris része csak az öncsillapítások alapvető harmonikáját adja át, akkor ez a harmónia csak a nemlineáris elem kimeneténél érdekes. Emiatt kibővítjük a kimeneti oszcillációkat Fourier sorozatban, és elvetjük a magasabb harmonikusokat. Ennek eredményeképpen:
Az (12.2) kifejezést egy későbbi felhasználásnál kényelmesebb formában újraírjuk, és a (12.1) pontból nyert u következő kifejezéseket helyettesítjük:
Ha ezeket a kifejezéseket (12.2) helyettesítjük, akkor:
Itt bemutatjuk a jelölést:
A differenciál-egyenlet (12.5) a szinuszos bemeneti jelre (12.1) érvényes, és meghatározza a nemlineáris egység kimenőjelét anélkül, hogy figyelembe venné a magasabb harmonikusokat.
Szerinti koefficiensek kifejezések (12.3) a Fourier-együtthatók funkciók a DC összetevőjét az amplitúdó és a frekvencia oszcillációja NONLIN ?? eynogo szintű bemenet. A fix A esetén a (12.5) egyenlet lineáris. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, ha a magasabb harmonikákat eldobják, akkor a rögzített harmonikus jelhez az eredeti nemlineáris kapcsolatot egyenértékű lineáris értékkel kell helyettesíteni, amelyet a (12.5) egyenlet ír le. Ezt a helyettesítést harmonikus linearizációnak is nevezik.
Az 1. ábrán. A 12.4. Ábra vázlatosan szemlélteti ezt a kapcsolatot, amely két párhuzamos kapcsolatot tartalmaz.
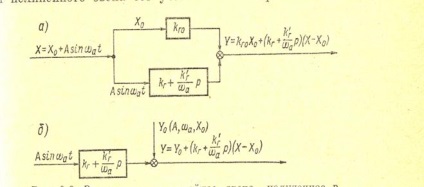
Ábra. 12.4. Harmonikus linearizáció eredményeként kapott egyenértékű lineáris kapcsolat.
Az egyik link () egy állandó komponenst és egy másik - csak az ön-oszcilláció szinuszos komponense.
Az együtthatókat harmonikus linearizációs együtthatóknak vagy harmonikus átviteli együtthatóknak nevezzük. - egy konstans komponens átvitelének együtthatója, és - két önműködő oszcilláció szinuszos komponensének két átviteli együtthatója. Ezeket az együtthatókat a nemlinearitás és az értékek és a (12.3) képletek határozzák meg. Vannak kész kifejezések ezekre a képletekre számos tipikus nemlineáris kapcsolatra. Ezek és általában minden inerciális nem inerciális összeköttetés esetében a mennyiségek nem függnek u-től, és csak az A és a amplitúdó függvényei.
A konstans komponense a kimeneti NONLIN ?? eynogo linket (. Lásd egyenlet 12.2, 12.4) jelenik meg egy két okból: ha a rendszert alkalmazzák állandó külső hatás, ami (. Lásd egyenlet 12,1), vagy ha a jellegzetes NONLIN ?? eynogo linket aszimmetrikus tekintetében a koordináta kezdete, amelynek eredményeképpen a bemeneti szinuszos jel helyesbítési jelensége következik be.
Az ilyen jellemzőkkel rendelkező nemlineáris kapcsolatok harmonikus linearizációjával a harmonikus linearizáció együtthatójával nem lehet kifejezni, formában
mivel itt és együtt. Ezért aszimmetrikus nemlinearitások esetén nem használhatunk egyenletet (12.5), de a (12.4) egyenletet kell használni. A megfelelő sémát az 1. ábra mutatja. 12.4, b. Ebben a vonatkozásban az ilyen nemlinearitások helyett a kifejezések közvetlen kifejezése.
Külső hatás és szimmetrikus jellemző hiányában az állandó komponens és egyenlet (12.4) a következő alakú:
hol van egy egyenértékű lineáris kapcsolat átviteli függvénye, amelyet egy nemlineáris egység harmonikus átviteli függvényének nevezhetünk.
Tehát a harmonikus linearizációval a nem-lineáris kapcsolatot egy lineáris kapcsolattal helyettesítjük, ami egyenértékű a bemeneti jel állandó komponensével és megközelítőleg egyenértékű az oszcilláló komponensével. Ebben az esetben megközelítőleg feltételezzük, hogy a bemenőjel vibrációs komponensének spektruma egyetlen harmonikusból áll, és a nem-lineáris kapcsolat torzulását elhanyagolják.
A linearizációs módszer zárt rendszerben való alkalmazhatóságának feltétele az aluláteresztő szűrő szerepe a rendszer lineáris részével. A sávszélességnek kicsinek kell lennie az auto-oszcilláció magasabb harmonikájához képest.
A harmonikus linearizálás segítségével meghatározhatjuk az esetleges önsugárzások paramétereit a számunkra érdekes rendszer pontján, amelyet felhasználhatunk egy nemlineáris rendszer stabilitásának, a tranziens folyamatok minőségének meghatározására.