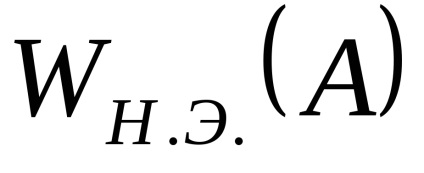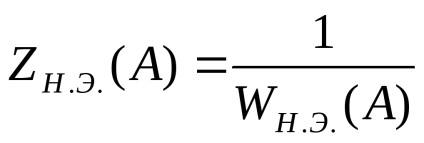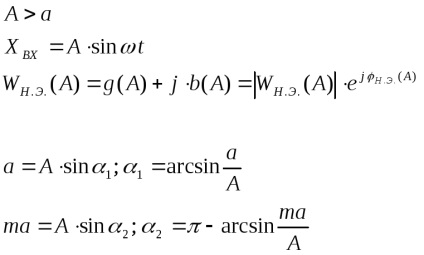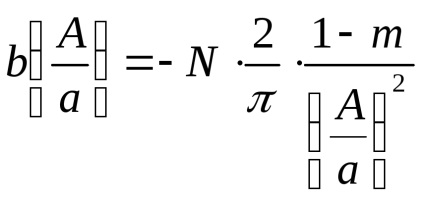Harmonikus egyensúlyi módszer (harmonikus linearizáció, szűrési módszer)

Az az elképzelés, a módszer abban áll, linearizálása nemlineáris, így a linearizáló együtthatókat függ a bemeneti jel amplitúdója, vagyis a nemlinearitásra helyébe „sugár” a lineáris, a lejtőn, amely függ a bemeneti jel. Ez a módszer pontos és alkalmazható mind jelentéktelen és jelentős a nemlineáris (Krilov-hierarchia módszer).

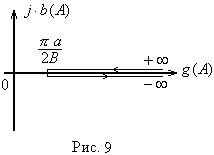
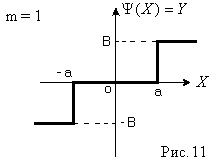
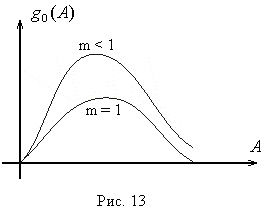
A módszer elgondolása azon a tényen alapul, hogy sok rendszer lineáris része jó szűrési tulajdonságokkal rendelkezik, azaz egy aluláteresztő szűrő. Ezt a tulajdonságot inerciális és integráló kapcsolatokkal látták el, amelyek frekvenciaválaszát az 1. ábrán mutatjuk be. Amelyből a lineáris részből áll

Ha bővítjük a kimeneti jel a nemlineáris rész (3. ábra) a Fourier-sor, akkor feltételezhetjük, hogy a lineáris része halad csak az első harmonikus bomlás szűrők és mások, és ezért, a kimenet a lineáris része a harmonikus jel marad. Így a harmonikus egyensúly módszer is egy eljárás linearizáló, ahol a nemlineáris jel a bemeneti lineáris részének (és ennélfogva a kimenet a nemlineáris rész) helyébe egy lineáris jel - az első harmonikus a nemlineáris jel gyengülésében. Az ilyen linearizáció érvényessége annál nagyobb, annál nagyobb a lineáris rész szűrési tulajdonságai.

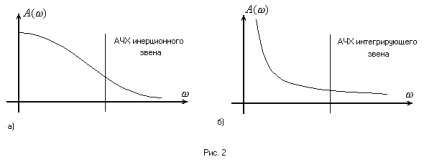
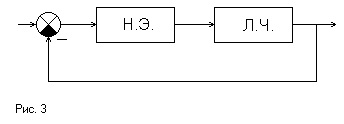
Így egy harmonikus linearizáció esetén az igazi nemlineáris elemet (NE) helyettesíti egy ideális, amelynek kimeneti jele megegyezik a valós NE kimenőjelének Fourier-expanziójának első harmonikájával.

harmonikus linearizációnak feladata, hogy meghatározza a komplex erősítés egyenértékű NE (harmonikus együttható, amely leírja a funkciót) képviseli a komplex átviteli együttható ideális NE, amelynek kimenete az első olyan harmonikus a Fourier sorfejtés a valós kimenő jel NE.

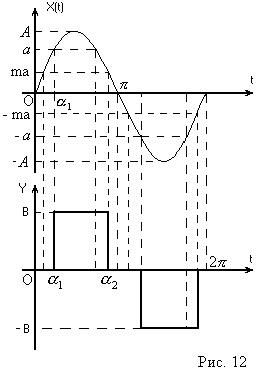
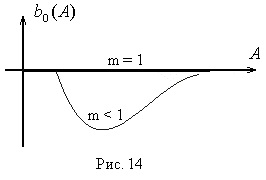
Feltételezzük, hogy harmonikus jelet adunk az NE bemenetére, amely a lineáris kimenet kimenete (4. ábra)

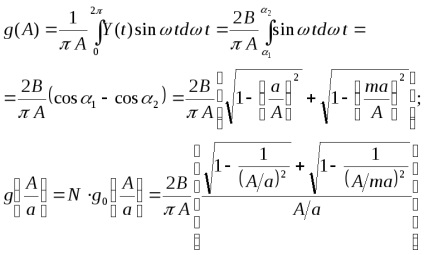
Bontjuk a kimeneti jelet. a Fourier-sorozatban, és csak az expanzió első harmonikusát tartja meg (a legtöbb nemlinearitást

- nem igaz).

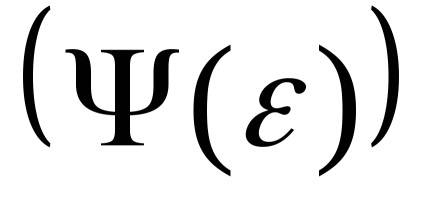
(mert a függvény páratlan, akkor

, második, negyedik stb. a harmonikusok nulla)

- nemlineáris elem komplex átviteli együtthatója

,

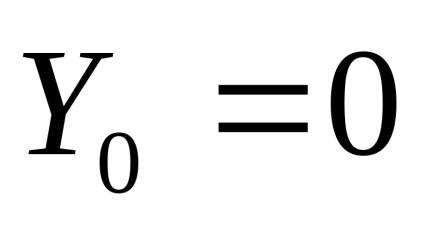
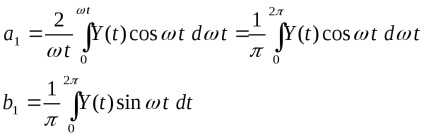
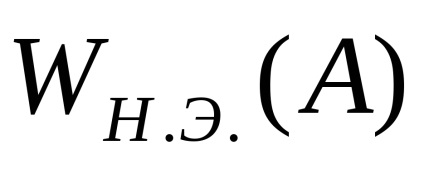
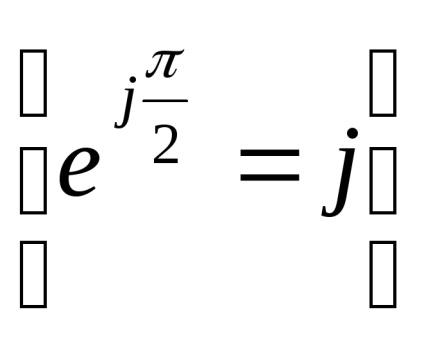
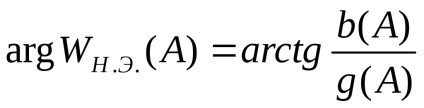
Megjegyzések: Abban az esetben, ha a nem-linearitás ferde szimmetrikus és nem tartalmaz kétértelműséget, a kimeneti jel első harmonikusja egybeesik a bemeneti jel fázisában, azaz nem tartalmaz koszinusz komponenst;

.

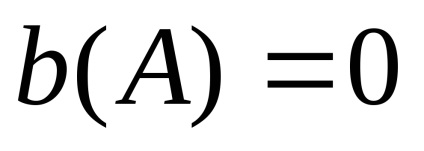
A linearizáció után az N.E. Tart az alábbi űrlapot:

talál

, ha a nemlinearitásnak van forma (5. ábra)

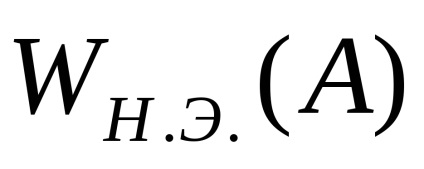
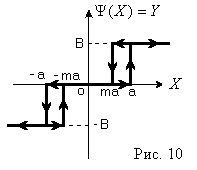
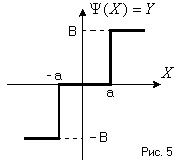
A nemlineáris elem bemenete szinuszos jelet kap, majd Y a forma harmonikus függvénye (6. ábra)

A nem linearitás, ahogy az a 4. ábrán látható. A 6. ábrán az eredethez képest ferde szimmetrikus, és nincs kétértelműségi zónája

, és a nemlineáris elem egyenlete a következőképpen alakul:

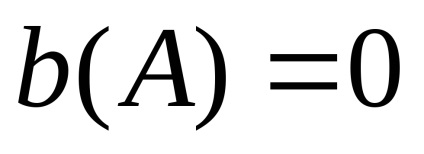
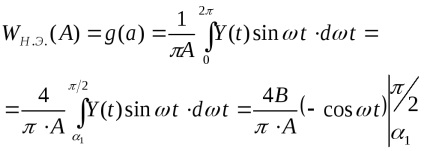
Az 1. ábrából. 6 látható, hogy mikor

;, majd,.

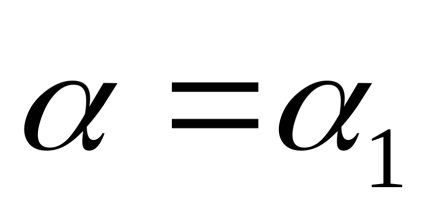
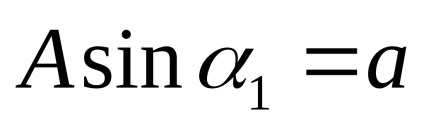
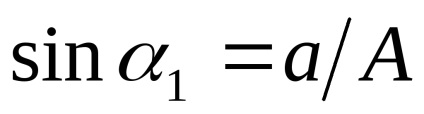
Kényelmes egyenértékű komplex nyereség bemutatása a bemeneti jel dimenzió nélküli amplitúdójának függvényében

, majd

- egy nemlineáris elem jellemzőjét reprezentáló normalizáló tényező;

- normalizált egyenértékű komplex átviteli együttható

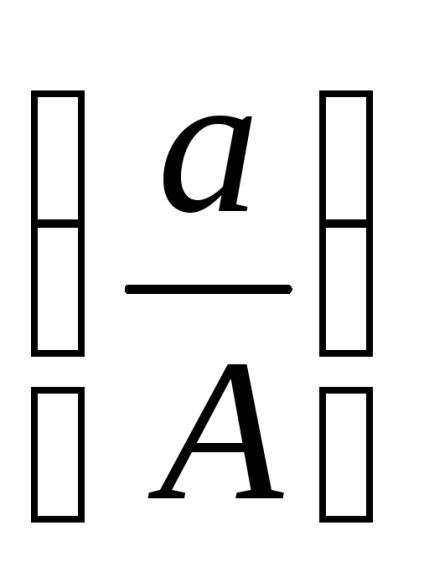
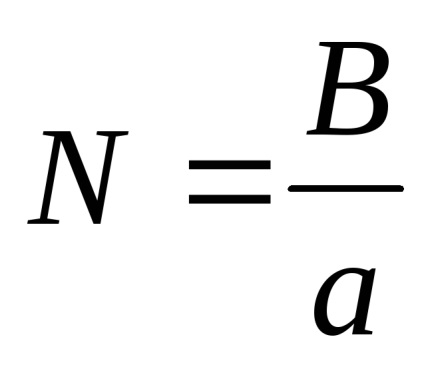
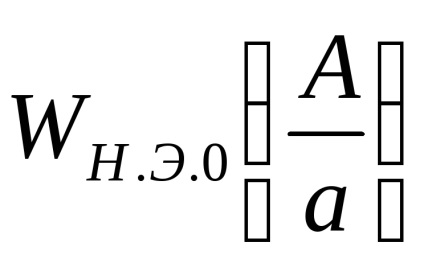
Az ilyen reprezentáció előnye az, hogy

csak egy változótól függ - a dimenzió nélküli amplitúdó, és annak értékeit lehet tabulálni.

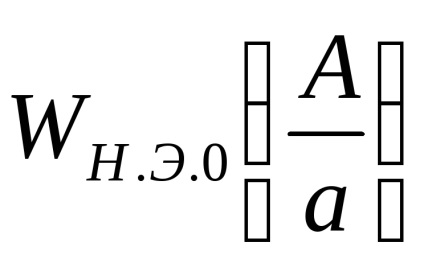
menetrend

van a formája (7. ábra)

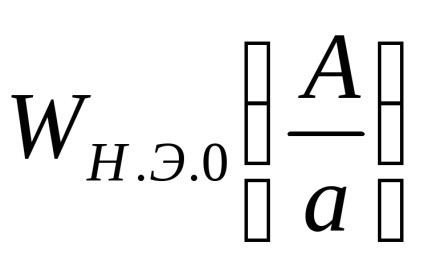
A <а выходной сигнал нелинейного элемента отсутствует (зона нечувствительности), следовательно

.

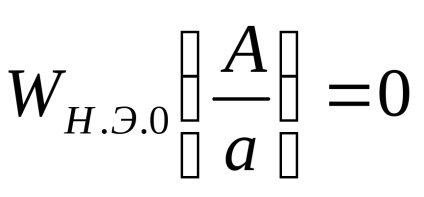
a

a nem lineáris elem kimenőjelének egyenlő B = const,, azaz a függőség szélsőséges.

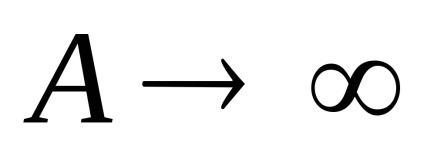
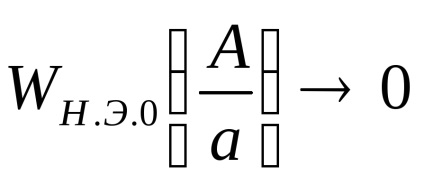
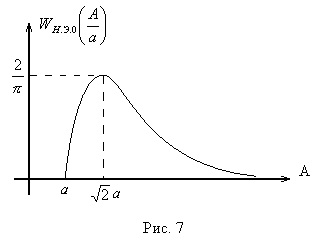
Találjuk meg a végletet

. Jelölje:

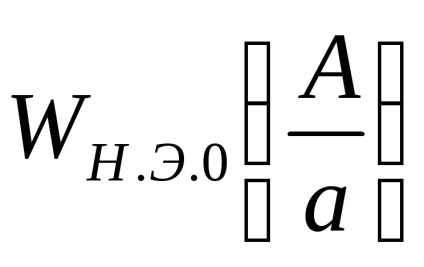
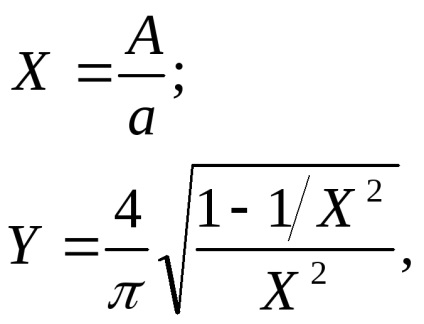
Találjuk meg a végső pontot, azaz Az X értéke, amelynél

.

,

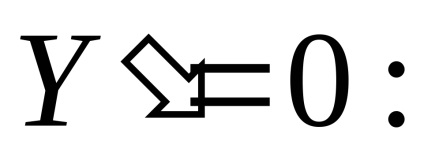
azaz a

van egy szélsőséges:

;

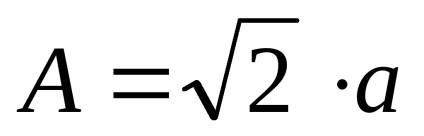
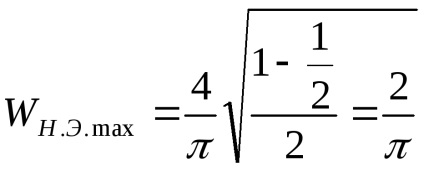
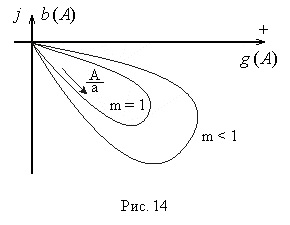
A vektor végének pontjai geometriai helye

A komplex síkban, ha az A bemeneti jel amplitúdója 0 és 0 között változikegy egyenértékű összetett átviteli együttható vagy egy nemlineáris elem amplitúdójának hodográfiája. Ez a funkció van beépítve, ugyanúgy, mint a hagyományos APFC, hanem funkciója az amplitúdó. Ebben a példábanés az amplitúdó karakterisztika egybeesik a tengellyel (8.

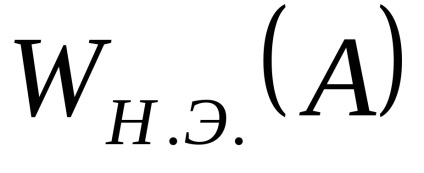
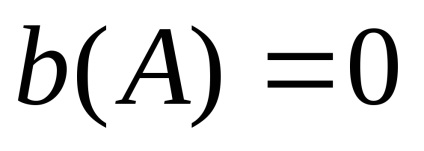
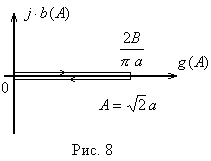
A nemlineáris elem inverz amplitúdó tulajdonsága a vektorra inverz vektor

:(9. ábra).

;

Kapcsolódó cikkek

• A harmonikus linearizáció ötlete

• A harmonikus linearizáció eszméje - a stadopedia