Diszkrét elemzés
A grafikonelmélet olyan matematikai objektumokat vizsgál, amelyek leírják a véges sorozatok elemei közötti kapcsolatokat.
Hosszú ideig a grafikonelmélet egyéni problémái olyan szórakoztató feladatokként jelentek meg, amelyeket könnyedén megfogalmaztak, de valamilyen oknál fogva nagyon nehéz megoldani. E problémák közül a hét Koenigsberg-híd problémája a leghíresebb.
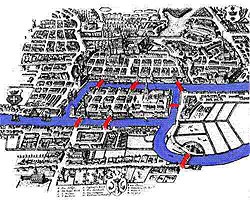
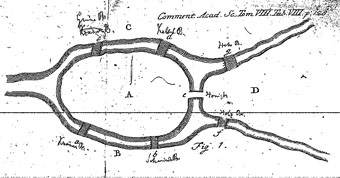
Különösen örülök annak, hogy emlékszem erre a könyvre - azonnal elolvastam, még franciául (amit nem tudok), és jelentősen használtam a mathmeha tanításánál. Így a terminológiánk és a megközelítésünk lényegében követi Berg könyvét, bár most sok könyv írja le a hazai és a külföldi, elméleti és alkalmazott grafikonok elméletét.
A kezdeti definíció elhanyagolhatónak tűnik
A szám háromszoros. ahol M egy nem üres véges készlet, N egy véges halmaz, és T egy N-től M × M-ig terjedő térkép.
Nem világos, hogy ez miért szükséges. Most kitaláljuk. Minden attól függ, hogy milyen jelentéssel bír ez a jelölés.
Az M elemeit a gráf csúcsainak nevezik. A csúcspontok nem lehetnek üresek.
Az N készlet elemeit a grafikon íveként hívjuk. A T leképezés mindegyik ívet rendezett pár csúcsokkal társítja. Ezek közül az első az ív kezdete, és a második az ív vége.
És a legfontosabb dolog: a grafikon grafikusan ábrázolható. hasonlítsa össze egy pont, körök vagy más figurák csúcspontjaival, és illessze össze a vonalakat ívekkel. Minden ívet az ív elejétől a végéig futó vonal képviseli. A vonal alakja és az ábrákon levő csúcsok elrendezése önkényes. Bizonyos értelemben az elejétől a végéig terjedő irányt jelez a sorban vagy mellette.
Azt mondják, hogy az ív kezdete és vége, és ez a két csúcs járulékos az ívhez. A véletlenszerű szó "inherens".
Az adott csúcsra ható ívek sorát csillagnak nevezik. Kényelmes beszélni a bejövő ívek csillagáról és a kimenő ívek csillagáról.
A diagram alatt négy különböző módon ábrázolható.
Az ív sajátosságai által okozott másik meghatározás 5.
Egy ív, amelynek kezdete és vége egybeesik, huroknak hívják. Az Arc 5 egy hurok.
Tegyük fel, hogy kaptunk egy grafikont. N legyen N részhalmaza.
A gráfot egy gráf részleges grafikonak nevezik.
Ebben a példában, ha a N '= értéket választja. megfelelő részleges grafikon jelenik meg a jobb oldalon látható (egy ív hiányzik a részleges grafikonon dolgozzák világosszürke) Egy példa az azonos részgráfja egy grafikon megfelelő M „= A, B, D>. a grafikon az egyszerű útvonal (k link), ha
1. | N '| = | M '| - 1 = k.
2. Az M 'elemek számozása 0-tól k-ig terjedő számok és N' elemek számozásával lehetséges 1-től k-ig. hogy minden ív N N 'az egyenlők
num (j) = szám (iEnd (j)) = num (iBeg (j)) + 1.
Így a meghatározás megfelel az útvonal vizuális ábrázolásának: a kezdeti zérusponttól az utolsóig terjedő nyilak által jelzett irányba halad.
Egy nulla számmal rendelkező csúcsot nevezünk az út kezdetének. és az utolsó csúcs az út vége.
A második meghatározás. Az út a "zavaros" nyilakkal, ahol bizonyos szakaszokon a megjelölt irány felé halad.
A grafikon a lánc (a k link) lánca, ha
1. | N '| = | M '| - 1 = k.
2. Az M 'elemek számozása 0-tól k-ig terjedő számok és N' elemek számozásával, 1-től k-ig terjedő számokkal lehetséges. hogy bármelyik ív N N 'esetében a következő egyenlõségek is fennállnak
num (j) = szám (iEnd (j)) = num (iBeg (j)) + 1.
vagy
num (j) = szám (iBeg (j)) = num (iEnd (j)) + 1.
Két ilyen számozás van a lánchoz: a végpontok bármelyike származhat. Valamennyi ívlánc pozitív és negatív részre oszlik - amelyben a kezdeti csúcsról az utolsóig mozogva a nyíllal haladunk, vagy a nyilakkal találkozunk. A legkisebb és legnagyobb számmal rendelkező csúcsokat a lánc extrém csúcsainak nevezik. Azt mondják, hogy a lánc összeköti extrém csúcsait.
A harmadik meghatározás. "Zárt út", amely ellentétben az út meghatározásával, az elején és a végén egybeesett, és a csúcsra vonatkozó információkat elfelejtették.
a grafikont kontúrnak (link k) nevezik, ha
1. | N '| = | M '| = k.
2. Lehetőség van felsorolni az M 'elemeket és az N elemeket 1-től k-ig terjedő számokból. hogy minden ív N N 'az egyenlők
num (j) = num (iEnd (j)) = num (iBeg (j)) + 1 mod k.
Az ilyen számok száma k-val egyenlő - a csúcsok bármelyike származhat.
A negyedik meghatározás. Ez az objektum egy lánc és egy kontúr tulajdonságait ötvözi.
a grafikon ciklusnak (a k linknek) nevezett, ha
1. | N '| = | M '| = k.
2. Lehetőség van felsorolni az M 'elemeket és az N elemeket 1-től k-ig terjedő számokból. hogy bármelyik ív N N 'esetében a következő egyenlõségek is fennállnak
num (j) = num (iEnd (j)) = num (iBeg (j)) + 1 mod k.
vagy
num (j) = szám (iBeg (j)) = num (iEnd (j)) + 1 mod k.
Az ilyen számok száma 2 × k - a csúcsok bármelyike származhat, és a számlálás két irányban történik.
Az első meghatározásban egy egyszerű módszert mondtunk. mivel lehetséges egy bonyolultabb konstrukció bevezetése, olyan ívekből álló átmeneti sorozatok, amelyek többször is előfordulhatnak a szekvenciában. Ezeket az átmeneteket össze kell hangolni - az egyes ívek kezdete, kivéve az első az előző végét. A csúcsok többször is megjelennek az úton.