Kör és Kör absztrakt
Az ókori Görögországban a kör és a kör tekintették a tökéletesség koronáját. Valójában minden egyes pontján a kör ugyanúgy rendeződik, ami lehetővé teszi, hogy egyedül mozogjon. A kerék ezen tulajdonsága lehetővé tette a kerék megjelenését, mivel a tengely és a kerékagy mindig érintkezésben kell lenniük.
A kör sok hasznos tulajdonságát tanulmányozzák az iskolában. Az egyik legszebb tétel a következő: rajzoljon egy adott ponton egy egyenes vonalat, amely metszi egy adott kört, majd a távolságok termékét ebből a pontból
Egy egyenes vonalú kör metszéspontja nem függ attól, hogy az egyenes vonalat hogyan rajzolták ki. Ez a tétel körülbelül kétezer éves.
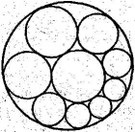
Az 1. ábrán. A 2. ábra két kört és egy láncot tartalmaz, amelyek mindegyike két láncot és két szomszédot érint meg egy lánc mentén. Jacob Steiner svájci geometriája körülbelül 150 évvel ezelőtt igazolta a következő kijelentést: ha a harmadik kör bizonyos választása lezárja a láncot, bezárja a harmadik kör bármely más választását. Ebből következik, hogy ha egyszer a lánc nincs bezárva, akkor nem zárul be a harmadik kör választása nélkül. Az illusztrált láncot festő művésznek keményen kell dolgoznotnia ahhoz, hogy megkapja, vagy forduljon a matematikához, hogy kiszámítsa az első két kört, ahol a lánc bezáródik.
Először említettük a kereket, de még a kerék előtt a kerek rönköket is használták - a súlyok hordására szolgáló görgőket.
Válassza ki a helyes kijelentéseket a kép alapján:
1) A C, B és E pontok nem tartoznak a körhöz.
2) A D, B és O pontok a körhöz tartoznak.
3) Az A, B és O pontok a körhöz tartoznak.
Hamis. A B pont a körhöz tartozik, mivel a kör része a körnek. Hamis. Az O pont a kör középpontja, de nem fekszik rajta.
1) Az O pont a kör és a kör középpontja.
2) Az O pont a kör középpontja, de nem a kör középpontja.
3) A D és B pontok nem tartoznak a körhöz.
1) A B és D pontok nem tartoznak a körhöz.
2) Az A, B, D és O pontok a körhöz tartoznak.
3) A B, D és E pontok a körhöz tartoznak.
Hamis. Az O pont a kör és a kör középpontja. Hamis. A D és B pontok a körhöz tartoznak. Hamis. A B és D pontok a körhöz tartoznak, mivel egy körön fekszenek, és egy kör része.
1) A B és D pontok osztják a kört 4 ívre.
2) A B és D pontok osztják a kört 3 ívre.
3) A B és D pontok osztják a kört 2 ívre.
Hamis. Az E pont nem tartozik a körhöz, mivel túl van a határon. Hamis. A B és D pontok osztják a kört 2 ívre. Hamis. A B és D pontok osztják a kört 2 ívre. Neverno. A misszió megvalósult.
Kör és kör - az egyik legrégebbi geometriai alak, ősi filozófusok nagy jelentőséget tulajdonítottak nekik. A kör a végtelen idő és tér megtestesítője, a létező szimbólum, az Univerzum. "A számok közül a legszebb a kör," gondolta Pitagorasz.
Körülöttünk sok kerek tárgy van. Képzeld el egy pillanatra, hogy hirtelen egy szerencsétlenség történt: minden a bolygón eltűnt! Úgy tűnik - legyen minden négyzet. Nem tudsz kerek csövek nélkül élni, és nem tudsz megszokni a négykerekű kerekekhez? Lehetséges-e elképzelni egy ember életét kör nélkül? Miért olyan sok testnek van egy kerek alakja? Annak érdekében, hogy ezekre a kérdésekre válaszokat találjunk, először is meg kell fontolnunk ezeknek a fogalmaknak a kialakulását és továbbfejlesztését.
A geometriai fogalmak eredete és fejlődése
A primitív emberek számára a körülöttük lévő tárgyak formája fontos szerepet játszott. Az alakban és a színben megkülönböztették az ehető gombákat a nem szántóktól, alkalmasak fák építésére, azoktól, amelyek csak tűzifa, finom diófélék keserű stb. Különösen finomak olyan kókuszpálmák, mint egy labda. Természetesen nem voltak különleges nevek a geometriai alakok számára. Azt mondták: "ugyanaz, mint a kókusz" vagy "ugyanaz, mint a só", stb. Tehát, a körülöttük lévő világ elsajátításával az emberek ismerkedtek a legegyszerűbb geometriai alakokkal.
Az ősi időkben kerek testek érdeklődnek az embertől. Az ókori Egyiptomban, a híres egyiptomi piramisok megépítéséhez még nem volt technikai szerkezet. Még a hatalmas kőtömbök csiszolását kézzel kellett elvégezni, és kerek rönkökkel mozgatta őket. Észrevettük, hogy könnyebb a gördülés, ha egy fából készült darabot szinte ugyanolyan vastagságban veszi fel az elején és a végén. Így az emberek megismerkedtek az egyik legfontosabb testtel - egy hengerrel. Hengeres, hengeres és a nők által használt, mosás utáni mosás. Az áruszállítás gördeszkázókon igen nehéz volt, hiszen a fák maguk súlyosan lemértek. A munka megkönnyítése érdekében a törzsekből vékony, kerek lapokat vágtak ki, amelyek könnyebben gördültek és segítettek a rakományt. Így jelent meg az első kerék. Sajnos a kerék közvetlen feltalálója ismeretlen.
Nem csak a munkafolyamat során az emberek különböző számokkal ismerkedtek meg. Régóta szeretik díszíteni magukat, ruhájukat, otthonukat. És sok, régen ékszeres ékszer, ez volt az alakja. A gyöngyök gömbölyűek voltak, a karkötők és gyűrűk kör alakúak voltak. Az ókori mesterek megtanultak szép formát adni bronz, arany, ezüst, drágakövek. A palotákat festő festők szintén körbejártak. A fazekas kerék találmánya óta az emberek megtanultak kerek eszközöket készíteni - edényeket, vázákat, amforákat. Körülbelül az épületeket támogató oszlopok voltak.
Az egyiptomiak és a babilóniaiak matematikai ismerete szétszóródott, és egy szabálycsomagot képviselt, amelyet a gyakorlatban teszteltek. Az ókori Görögországban az összes szétszórt tudás vezetett a rendszerhez, a geometria gyorsan fejlődött, mint tudomány. Csak az ókori Görögországban, a "kör" és a "kör" kapta a nevüket, a görög eredetű geometriai alakok szinte minden nevét, mint magát a geometria szót ("geo" - föld és "metrio"). Azonban ezek a szavak nem az orosz nyelvből származtak, hanem közvetlenül a görögül, de latinul.
Az ókori Görögországban a figurák számos tulajdonsága, beleértve a kört és a kört, tételek formájában formálódtak és bizonyítottak. Geometria, mint a geometriai alakok tulajdonságainak tudománya, a görög Euclid tudós (Kr. E. III. Század) leginkább a "Elements" című könyvében írta le. Sok évszázadon keresztül a "Beginnings" volt az egyetlen oktatókönyv, amelyen a fiatalok geometriát tanultak. És még most is, a mi korunkban a tankönyveket az Euklid "alapelvei" nagy hatása alatt írják.
A kör és a kör lapos alakú. Három dimenzióban élünk. És milyen geometriai testben válik a kör és a kör, ha az űrbe esnek? Ez egy gömb és egy labda. A "gömb" - a görög "sfayra" szóból származik, fordításban - "golyó". Ezen túlmenően, a tér geometriáját tekintve más kerek a szervezetben - a „henger” (a görög szó „kyulindros” azt jelenti, hogy „roll”, „roller”) és a „kúp” (a görög szó „Konos”, azaz „fenyőtoboz”) . A kerek testek között a legfontosabb volt a labda.
Így az ókori Görögországban a kör és a kör tekintették a tökéletesség koronáját. "Mindegyik pontján a kör ugyanúgy rendeződik, ami lehetővé teszi számára, hogy egyedül mozogjon." A kör tulajdonsága lendületet adott a kerék megjelenésének. .
Kör - "körkörös" - a latin szó, innen és "iránytű", amely nélkül nem építettünk volna egy kört. Az iránytű és a vonalzó a legrégebbi rajzeszközök a Földön.
Kör és kör elemek:
Olyan szegmens, amely összeköti a kör közepét bármelyik pontjával (latinul - a kerékről beszélt).
A kör átmérője az akkord, amely áthalad a kör közepén (görög - "átmérő").
A kör akkordja egy olyan szegmens, amely összeköti a kör két pontját (egy görög vonallal).
Egy ív egy kör része, amelyet két pont határol.
Gyakran a gyakorlati feladatok során ismernie kell egy kör kerületét. És hogyan kell megmérni a kör hosszát, ha maga a kör ívelt vonal, és a hosszegység egy szegmens? Számos lehetőség van a kör kerületének mérésére.
Azonban ezek a közvetlen mérési módszerek a kerületen nem túl kényelmesek és közelítő eredményeket adnak. Ezért már a régi időkből kezdtünk keressük a tökéletesebb mérési módszereket. A mérések során azt tapasztaltuk, hogy a kerület és az átmérő hossza határozott összefüggést mutat: C: d ≈ 3.1.
Számos tudós - a matematikusok megpróbálták bizonyítani, hogy ez az arány egy állandó szám, nem attól függően, hogy a kör nagysága milyen méretű, kezdetben görög betűvel π-ο a görög "periféria" - egy kör.
C: d = π, ahol C a kerület, d az átmérő hossza, tehát a C = πd vagy C = 2πr képlet körhosszúsága.
A matematikusok kutatását követően a következő méréseket és számításokat végeztük:
1. Számolja ki a pi számot. a) vékony fonal segítségével mértük egyes háztartási cikkek kerületének C hosszúságát; b) Ha pontosabban megtalálja a dimmer d hosszát, csatolja ezt az objektumot egy papírlaphoz, és rajzoljon egy félig levágott, félbehajtott ceruzát, a vonalvezetéshez mért átmérőt; c) megtalálta a C: d arányt, az adatokat bevittük a táblázatba:
A C hosszúsága
2. A pi. Szám értékének határértékei. a) iránytű segítségével a kört egy négyzetbe írták: ha az átmérő 1, akkor a kerülete egyenlő a π-vel. Az 1. oldalon lévő négyzet kerülete 4. Így π kisebb mint 4. (1. ábra). b) a jobb hatszöget ugyanabba a körbe adtuk: a kör átmérője ismét 1, a kerülete π. A szabályos hatszögnek az oldala megegyezik a sugárral, azaz 0,05, a perem pedig 6 · 0,5 = 3, akkor π nagyobb mint 3 (2. ábra).
Ennek eredményeképpen meggyőződésünk volt, hogy a kör hosszának és átmérőjének (π szám) aránya állandó szám és 3 <π <4, megerősítettük a tudósok - a matematikusok - kutatását.
π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ....
Miért kell π-vel, és ilyen pontossággal? A π szám rendkívül fontos a tudósok és a mérnökök számára. Minden, ami kerek, és minden, ami mozog egy körben (mint kerék vagy bolygó) tartalmaz π. Π nélkül az emberek nem tudtak autókat létrehozni, megérteni a bolygók mozgását, vagy számolni, hogy hány borsó illeszkedik egy ónkádba. De a rejtélyes szám rejtélye ma nem oldódik meg, és még mindig izgatja a tudósokat. Jelenleg a π szám a nehéz formulák, a matematikai és a fizikai tények csoportjához kapcsolódik. Számuk továbbra is gyorsan növekszik. Mindez a növekvő érdeklődést jelzi a legfontosabb matematikai konstans iránt, amelynek tanulmányozását több mint huszonkét évszázadban számolták.
Miután tanulmányozta az irodalmat és elvégezte saját mérési tanulmányainkat egy kört és körben, a következő következtetésekre jutottunk: a kör és a kör meglepően harmonikus. A kör az egyetlen olyan görbe, amely "önmagában csúszik", a centrum körül forog. Ez a kör tulajdonsága adja meg annak a kérdésnek a kérdését, hogy miért használják az iránytűket a rajzoláshoz, és miért kerekek a kerekek, nem négyszögek vagy háromszögek.
Kör a környező életben.
A kör szerepének feltérképezése a környező életben, kérdőíves felmérést végeztünk az 5-9. Évfolyamos diákok és a Moszkvai Oktatási Iskola tanárai (összesen 90 fő):- Milyen kerek testeket látsz az életedben?
- Mi a másik jelentőségű a tudományágban?
- Milyen gyakorlati feladatai vannak a mindennapi életben a kör és kör ismerete alapján?
- Miért gondolod, hogy olyan sok kerek test van a természetben?
Az első kérdésre adott válaszokat be kell mutatni.
A tantárgyi tanárok válaszai a kérdőív második kérdésére rájöttünk, hogy a kör nemcsak a matematikában, hanem más tudományokban is nagy jelentőséggel bír: