Hogyan oldjuk meg ezt a problémát a fizikában, milyen képleteket használunk itt

Egyszerűbb megoldást találtam a problémára. Lásd a rajzot.

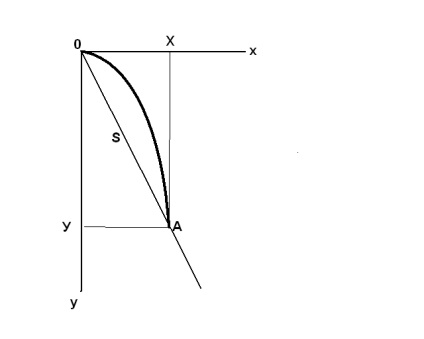
Kő esik egy parabola (félkövér görbe), és esik a meredekség A. X és Y - pont koordinátáit A. Azaz, az X - elfogadott egy kő út mentén a x-tengely, és Y - módon az Y-tengelyen az X-tengelyen (vízszintes ) a kő állandó sebességgel mozog, Vx = 8 m / s. Az y tengelyen kő a földre esik (azaz függőlegesen) ereje által Föld gravitációs sebességgel VY = GT, ahol g = 9,81 m / s - a nehézségi gyorsulás, és a T - idő. Az x tengely mentén haladt útvonalat a képlet határozza meg

Az Y tengely mentén haladva (egyenletesen gyorsított mozgás)

Nézzük meg a pályának az egyenletét, amely mentén a kő mozog (az ábrán a vastag vonal). Ehhez ki kell küszöbölnünk az t időt az (1) és (2) egyenletekben. Az (1) egyenletből t = x / Vx. A (2) egyenletben helyettesítjük, amit megkapunk

Vagyis, az x függ a x a négyzetben. És ez a parabola egyenlet. Most meg kell találnunk az A (X és Y) pont koordinátáit, ahol a kő a lejtőn esik. Ehhez ismerni kell a lejtési egyenletet (ferde sík vagy 0A vonal az ábrán). E ferde egyenes (y = kx) egyenlete

y = tg (-60 °) * x = -sgrt3 * x = -1,732x, (4)

mivel a tangens -60 ° = -sgrt3 = -1,732. -60 ° az X0A (negatív) szög, abszolút nagyságú a 0AV = 60 ° szögnél. A sgrt a négyzetgyöket jelöli. A (3) és (4) egyenletekből (g / 2) (x / Vx) ^ 2 = 1,732 h. Ezért találjuk

X = 2 * 1,732 * (Vx ^ 2) / g = 22,60 m (5)

mivel sebességünk Vx = 8 m / s. Ezt az X-et a (4) egyenletbe helyezzük

Y = -39,14 m. A szám negatív, mivel a távolságot az x tengelytől lefelé mérjük. X és Y a háromszög lábai. Megtaláljuk a Pythagoras tételét 0A = S hypotenuse-t

A (4) -ből Y = -sgrt3 * X, majd Y ^ 2 = 3X ^ 2. A (6) -ból azt találjuk, hogy S ^ 2 = X ^ 2 + Y ^ 2 = 4X ^ 2. Ezért van S = 2X. Az (5) segítségével S = 45,2 m-t kapunk. A válasz 45,2 m.

Ha dobott egy kő (vagy bármely szervezetben) vízszintes kő részt kétféle mozgás. Ugyanakkor a légellenállást elhanyagolják, ami a testmozgás alacsony sebességén is elvégezhető. 1) A kő vízszintesen, állandó sebességgel Vr = 8 m / s. Ezért, a kő vízszintesen tartják (legyek) t idő = Vr path Sg * t. 2) Ha csak elengedte a kő (azaz a kezdeti sebesség 0, a kő esik le a földre függőlegesen. Tudjuk fizika, hogy a mozgás lesz egyenletesen gyorsuló a nehézségi gyorsulás g = 9,81 m / s ^ 2 Az arány csökkenése növekedni fog az idővel a következő képlet szerint Vb = GT. Ezen az úton SB alatt megtett t nulla kezdeti sebességet képlet szerinti fizika SB = g (t ^ 2) / 2. a mozgási útvonal egy parabola. egy bizonyos ponton a parabola metszi a átfogója Háromszög a képen? Hagyja a háromszöget a hypotenuse hossza távolság mentén a lejtőn, hogy a pont sziklaomlás Ezután a hossza a bal lába van a megtett távolság függőlegesen SB, és a hossza a lábszár - .. a megtett távolság kő Sg vízszintes tól trigonometria, tudjuk, hogy az érintő a jobb alsó sarokban (60 ° C) egyenlő az arány a bal lábát az alsó, azaz a tg60 ° = SB / Sg = [g (t ^ 2) / 2] / Vr * t = GT / 2Vg De tg60 ° = sgrt3 Amennyiben sgrt -... négyzetgyöke Tehát tg60 ° egyenlő a négyzet gyökere 3. ebből az egyenletből találunk időt kő mozgás eső lejtőn

t = (2Vr * sgrt3) / g = (2 * 8 * sgrt3) / 9,81 = 2,825 s.

Vagyis a kő 2,825 s-ra esik. Most meg kell találnunk, hogy milyen távolságban lesz a dobogótól a kő. Azaz, a lejtő távolság S. megtett távolság vízszintes Sg = Vz * t = 8 * 2825 = 22,6 m. Megtett távolság függőlegesen lefelé SB = g (t ^ 2) / 2 = 9,81 * (2,825 ^ 2 ) / 2 = 39,1 m. A lejtőn áthaladó út a képlet alapján található

S = sgrt (Sg + SB * 2 ^ 2) = sgrt (22,6 ^ 2 ^ 2 + 39,1) = sgrt (511 + 1529) = sgrt (2040) = 45,2 m.

Tehát a kő a lejtőn 45,2 m-re esik.

Aztán jött az a gondolat, hogy S könnyebben megtalálható. A háromszögből azt találjuk, hogy Sr = S * sin30 °. Ezért S = Sr / sin30 ° = 22,6 / (1/2) = 22,6 * 2 = 45,2 m.

bezde lnik [25.1K]

Ha nem vesszük figyelembe a légellenállás, a kő repül egy vízszintes sebesség Vr = 8 m / s és t időpontban esett a domboldalon repül vízszintesen Sg = Vz * t = 8 * t m. Ugyanakkor, a kő esik függőlegesen le a nehézségi gyorsulás egy = 9,81 m / s 2 és repülni függőlegesen SB = a * t ^ 2/2 = 9,81 * t ^ 2/2. Mivel a lejtő szöge 60 fok, a beesési pontjától a kő lejtőn Sg = SinS30 * SB = 1/2 * SB, és azt kapjuk a 8. egyenletben * 9,81 * t = t ^ 2/4, ahol t = 32 / 9,81s . Az egyszerűség kedvéért, veszünk egy = 10 m / s, akkor t = 3,2-c, Sg = 8 * 3,2 = 25,6 m

Sv = 2 * 25,6 = 51,2 m. A lejtő mentén található távolságot a Pythagorean-tétel Ssk = 57 m.