A megbízhatóság exponenciális törvénye
A kudarc veszélyének függvénye természetesen háromféle lehet:
1. A működési idő csökkenésével járó kiesés veszélye csökken.
Az elem növeli működésének megbízhatóságát. Ez a ritka eset fordul elő például az előzetes bevezetés folyamatában, amikor a kezdeti működési időszakban a hibás, hibás elemeket újak váltják fel. Az így kialakított elemkészlet növeli megbízhatósági jellemzőit.
2. A meghibásodás veszélye növekvő működési idővel nő. Az elem működés közben lebontja megbízhatósági jellemzőit. Az elem "öregszik". Ez egy nyilvánvaló, leggyakoribb eset.
3. A működési hibák veszélye nem változik, állandó marad. A működő elem "nem öregszik", "új" marad. Nyilvánvaló, hogy ez valamiféle elméleti modell.
Nézzük részletesebben az utóbbi esetet. Ha a # 955; (t) = const, majd (1.10) szerint megkapjuk
Az így létrejövő megbízhatósági törvényt exponenciálisnak nevezik, és nagy jelentőséggel bír a megbízhatósági elméletben. Az (1.3) szerinti hibaarány egyenlő
Az (1.11) szerinti hibák közötti átlagos idő
A megbízható működés valószínűségét kiszámítjuk az átlagos t = T0 hibaidőnek megfelelő intervallumban.
A megbízhatóság nagyon kicsi, az elemek körülbelül egyharmada működni fog. Ezért a felelős elemeknél a működési időt sokkal kisebbnek kell választani, mint az elem átlagos élettartama (t < és a kudarc valószínűsége megközelítőleg egyenlő A hiba valószínűsége kis időintervallumon belül # 8710; t a használható elem # 955; # 8710; t. Ez a valószínűség nem függ a munkaidőtől, ha az elem hangos, akkor további viselkedése nem függ a múltbéli történelemtől. A beszélgetés is igaz. A hibamodellek esetében, ha a történelem nem befolyásolja a hibák viselkedését, a megbízhatóság exponenciális törvénye érvényes. Ilyen kudarcokat neveznek a pillanatnyi károsodásnak.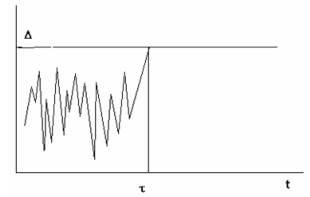
2.1 ábra Azonnali hiba modell.
Hagyja az elemet véletlen sokk túlterhelésen (2.1 ábra). Ha kevésbé kritikus # 8710; nincs kudarc, nem kisebb károsodás, rosszabb a megbízhatósági jellemzők. Az elem minden "indikátornak" marad. Amint a túlterhelés meghaladja a kritikus szintet, az elem meghibásodik. Ha a túlterhelés véletlenszerű folyamat, például a fehér zaj, amelynek összes mintája független, akkor a működési idő nem változik. Vagyis egy ilyen hiba modell megfelel a megbízhatóság exponenciális törvényének.
Az exponenciális törvény hátránya, hogy ritka hibás modellt tükröz. Azonban később lesz látható, hogy csak ez a törvény lehetővé teszi számunkra gyakorlati, mérnöki számítási módszerek kidolgozását.
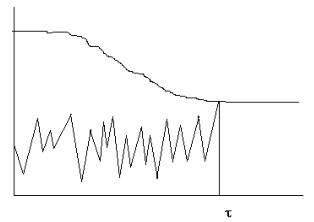
Ábra 2.2. Egy változó küszöbértékű rendszer.
Tekintsünk egy másik pillanatnyi károsodást, de időben változó küszöbértékkel (2.2. Ábra). Ez a séma eltér a 2.1 ábrán látható rendszertől, mivel a küszöbérték a megengedett túlterhelések változójának határa. Először nagyszerű és a túlterhelés soha nem érheti el. Ezután a küszöb csökken és egy pillanatban t0 egy bizonyos konstans értékre van rögzítve, amit túlterheléssel érünk el.
Nekünk van t T> t0 esetén a megbízhatóság exponenciális törvénye P (t) = e - # 955; (t-t0) A hibamentes működés valószínűségének grafikonját az 1. ábra mutatja. 2.3. 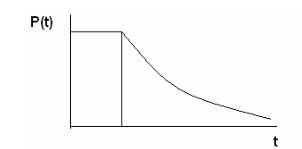
Ábra 2.3. Változó küszöbű törvény.
A hiba valószínűségének sűrűségével kapcsolatban (lásd a 2.4. Ábrát):
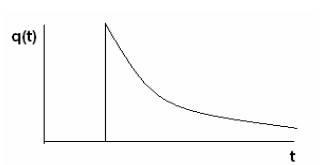
Fig.2.4. Kudarc veszélye.
Ez a modell közelítőleg szolgálhat a megbízhatósági törvény kísérleti meghatározásának eredményeihez, amelyeket a 2. ábrán bemutatunk. 2.5.
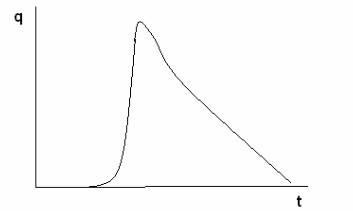
Ábra 2.5. Kísérleti hibaarány görbe.
1. Mi a megbízhatóság exponenciális törvénye?
2. Milyen arányban működik a problémamentes működés és a tényleges működési idő átlagos időtartama?
3. Mutassa be a pillanatnyi kár modelljét.
3. A károsodás modellje. Gamma - az üzemidő eloszlása
A károk felhalmozódásának modellje azt feltételezi, hogy a zavarok hatása a hasznosítási folyamatba, az elem kopása folyamatosan felhalmozódik, növekszik. Ez a felhalmozódás a véletlen apró termelési hibák miatt különböző kiindulási feltételektől indulhat, a hatások véletlenszerű jellege miatt eltérő ütemben nőhet, és így tovább.
Tegyük fel, hogy létezik egy állandó küszöbérték, amelyen a hiba bekövetkezik (3.1 ábra).
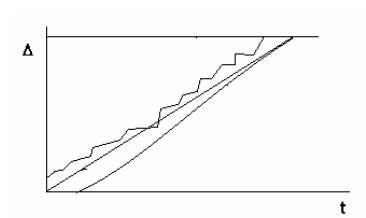
3.1 ábra. A károsodás modellje.
Vegyük figyelembe a károsodás következő modelljét (3.2 ábra).
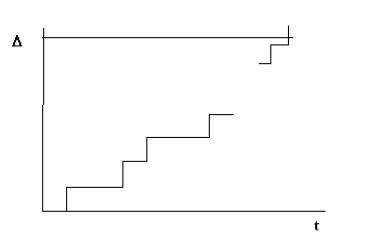
3.2 ábra. A károk felhalmozódásának elfogadott rendszere.
Véletlenszerű, független időbeli változások esetén a kár növekedése hirtelen történik. Minden ugrás egyenlő amplitúdóval. Az ugrás értéke egyenlő a. Azt is feltételezzük, hogy az ugrás és a küszöb közötti kapcsolat olyan, hogy az r ugrás után meghibásodás következik be. Hagyja, hogy az ugrások időpontjai egyszerű eseménysorozatot képezzenek, vagyis megfelelnek a következő feltételeknek: az események függetlenek; álló helyzet; egyszerre csak egy ugrás lehet. Ismeretes, hogy a legegyszerűbb áramlás vagy Poisson áramlás esetében a pontosan k események előfordulásának valószínűsége a T időben megegyezik
itt # 945; az ugrások átlagos gyakorisága.
A hiba az ugrások számának egészére esik. Ezután a P (t) - megbízhatósági függvény annak a valószínűsége, hogy t idő alatt kevesebb lesz, mint az ugrás
Találjuk meg az ilyen eloszlás esetleges hibáinak valószínűségét
A kétparaméteres (# 945; r) megbízhatósági törvényt kaptuk, amely közelítené a kísérleti jellemzőket. De ehhez szükséges a (3.3) kiterjesztése az r folyamatos értékére. Elvileg a (3.3) r mindenhol folytonos lehet, kivéve a faktoriális érvelést.
Van egy gamma függvény, amely az argumentum egész pozitív értékei esetében egybeesik a faktoriális értékkel, és elfogadható a faktor koncepció kiterjesztésének az argumentum nem egészének értékeire.
A gamma funkció kifejezése:
R pozitív egész számok esetén a gamma funkció értéke
A faktorikus függvényt a (3.3) gamma-függvény helyettesítve szerezzük be
Ezután a r folyamatos értékei esetén a hibák valószínűsége
és a megbízhatóság függvény
A kudarcok közötti átlagos időre vonatkozóan van
Itt a helyettesítés x = # 945; # 964, tehát d # 964; = dx / # 945;
A gamma függvény esetében van egy visszatérési összefüggés, amely a (3.5) -ból következik:
Aztán az átlagos élettartam (3.9) után:
Megjegyezzük, hogy a kapott eredmény egyezik az exponenciális törvény eredményével. A pillanatnyi kármodellek esetében elegendő egy esemény - elérni a küszöböt (r = 1), amely független a folyamat történetétől, hogy hiba történjen. A Poisson áramlás eseményeinek átlagos gyakorisága # 945; a valószínűség megegyezik a megbízhatóság exponenciális törvényének 1 / T0e kiesése közötti átlagos idő kölcsönösségével. ezért
Aztán az exponenciális törvénytől (3.11) megkapjuk az általunk ismert eredményt
Az élettartam diszperziójára már van
Itt figyelembe vesszük, hogy a (3.10)
A kudarc veszélye:
A megbízhatósági törvény kudarcának veszélyét komplex módon számolják ki. Azonban kis időben P (t) ≈ 1; e - # 945; t ≈1, akkor a (3.6) -ból következik, hogy az időzítés veszélyének függősége formában van # 955; (t) ≈At r -1. amely lehetővé teszi a meghibásodási veszély viselkedését a kezdeti időközönként. A pontos függőségek a 3.3 ábrán láthatók.
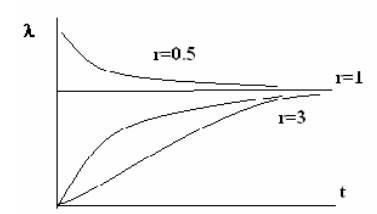
3.3 ábra. A hibák veszélyének függése a paraméteren.
R> 1 esetén az öregedési elemek modellje van (a meghibásodás veszélye növekszik). R = 1 esetén exponenciális megbízhatósági törvényünk van. Ez a pillanatnyi kármodellnek felel meg. Egy ugrás elég hiba esetén. Amikor r<1 имеем убывающую опасность отказа. Частота отказов представлена на рис.3.4. В пределе при r→∞ закон гамма- распределения стремится к нормальному закону надежности.
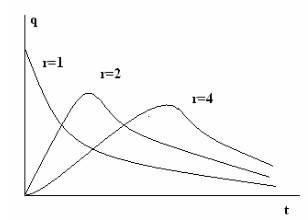
Ábra 3.4. A hiba valószínűségének sűrűsége a hibaarány.
1. Mutassa be az üzemidő gamma eloszlásának törvényi károsodásának modelljét?
2. Mi a gamma funkció, miért használják a gamma-eloszlás törvényének leírására?
3. Milyen formája van a kudarc veszélyének függvényében a gamma-eloszlás törvényében?