Oktatási portál
A fixpontos elektromos töltések (TZ) kölcsönhatásának törvényét 1785-ben alapította S. Coulomb (korábban ezt a törvényt G. Cavendish 1773-ban fedezte fel, és csaknem 100 évig ismeretlen volt). Az elektromos töltések közötti kölcsönhatást elektromos mező (EF) segítségével végezzük. Minden díj megváltoztatja a környező tér tulajdonságait, és benne egy EP-t. A mező a saját pontjainak erővel történő terhelésével jár el.
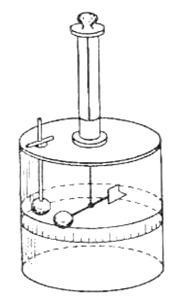
Egy pont (T3) olyan testre koncentrálódik, amelynek lineáris méretei elhanyagolhatóak, mint a más, töltött testekhez való távolsággal, amelyekkel kölcsönhatásba lépnek. A ponttöltés (TZ) ugyanazt a fontos szerepet játssza a villamosenergia-doktrinában, mint a mechanika MT (anyagpontja). Segítségével a torziós inga (ábra. 2.1), hasonlóak azokhoz, amelyek arra használták, hogy meghatározzák Cavendish gravitációs állandó változás Medál kölcsönhatás erő két töltésű szemcsék, attól függően, hogy a nagysága a töltés, és a közöttük lévő távolság. Ebben az esetben a medál alapja az volt, hogy amikor megérinti az azonos töltés nélküli golyó töltött fémgolyóját, a töltés egyenlően oszlik el a két golyó között.
Coulomb törvénye. A két rögzített T3 kölcsönhatásának ereje arányos az egyes töltések értékével, és fordítottan arányos a köztük lévő távolság négyzetével.
Az erő iránya egybeesik a töltőcsatornával.
(2.1) a vákuumban a T3 kölcsönhatásának rögzítésének vektorformája.
Ábra. 2.2. Coulomb erők
Írjuk le ugyanazok a pozitív díjak kölcsönhatásának modulusát q1 és q2:
hol van az az erő, amellyel a töltés q i a díjra hat? a fennmaradó (N-1) töltések hiányában.
A kapcsolatot (2.4) az elektromos mezők szuperpozíció elve (elrendelése) nevezzük.
A (2.4) képlet lehetővé teszi, hogy ismerjük a ponttöltések közötti kölcsönhatást, kiszámítsuk a véges méretű testekre koncentrált töltések közötti kölcsönhatást.
Ehhez meg kell szakítani a kiterjesztett test minden töltését ilyen kis díjakkal dq. úgy, hogy pontszerűnek tekinthetők, számítsuk ki a kölcsönhatás erejét a (2.1) képlet segítségével a dq. párban, majd vektoradagolást adunk ezeknek az erőknek - azaz. alkalmazza a differenciálódás és az integráció módját (CI). A módszer második részében a legnehezebb az integrációs változó kiválasztása és az integráció határainak meghatározása. Az integráció határainak meghatározásához részletesen elemezni kell, hogy mely változók függenek az ismeretlen mennyiség differenciájától, és melyik változó a fő, legfontosabb. Ezt a változót gyakran integrációs változóként választják ki. Ezt követően minden más változó a változó függvényeként fejeződik ki. Ennek eredményeképpen az ismeretlen mennyiség differenciája az integráció változójának függvénye. Ezután az integráció korlátai az integrációs változó szélsőséges (korlátozó) értékei. Egy meghatározott integrál kiszámítása után megkapjuk a keresett érték számszerű értékét.
Ez a módszer (CI) két elvre épül:
1) a törvény különböző formában való képviseletének lehetősége;
2) a szuperpozíció elvét (ha a törvényben szereplő mennyiségek additívak).