A logaritmikus függvény monotonitása - bemutató 230538-7

A logaritmikus függvény tulajdonságai >>

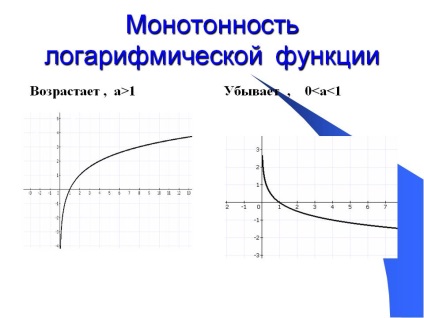
A logaritmikus függvény monotónitása. Növekszik. a> 1. Csökken. 0

Slide 7 a bemutató "Általános lecke a témában. "A logaritmikus egyenletek és egyenlőtlenségek megoldása" »

Méretek: 720 x 540 képpont, formátum. jpg. A lecke használatához egy ingyenes dia letöltéséhez kattintson jobb egérgombbal a képre, és kattintson a "Kép mentése másként" lehetőségre. ”. Töltse le a teljes bemutatót "Általános lecke a témában. „A döntés logaritmikus egyenletek és egyenlőtlenségek» .ppt »lehet zip-archívum mérete 605 KB.

Kapcsolódó bemutatók

"Logaritmikus egyenlőtlenségek megoldása" - Logaritmikus egyenlőtlenségek. Oldja meg az egyenlőtlenséget. A 11. osztály algebra.

"Funkcionális gráf létrehozása" - Az y = cosx +? / 2 függvényt használva. A grafikonok és függvények y = m sinx + n és y = m cosx + n. Az y = m * sin x függvény grafikonja. Az y = cosx függőleges görbék eltolódása. A feladatok példáihoz kattintson a l gombra. egérgombot. Az y = sinx függőleges függvény görbéi. Visszatérés a tartalomhoz kattintson ide. A folytatáshoz kattintson a l gombra. Az egérgomb.

"Funkciók 9 osztály" - Az elemi függvények osztályának kialakítása. Melléklete. Melléklete. 15. melléklet. 6. melléklet. 16. függelék. 11. melléklet. Bevezetés. 3. függelék. Grafikonok készítése. A funkció lehet meghatározni a következő képlet segítségével, például: y = 2x + 5, S = AT2 / 2, S = vt. A funkciók meghatározásának módszerei. A teljesítményfüggvény y = x-1.

"Logaritmikus egyenletek és egyenlőtlenségek" - Logaritmusok. A logaritmus meghatározása. Számoljuk. Jelölje meg a következő egyenletek megoldásának menetét. A logaritmusok és a logaritmikus függvények tulajdonságainak ismétlése. Összehasonlítás. Az új alapokra való áttérés formái. Tudja meg, hogy a szám pozitív vagy negatív. Képzettség a logaritmikus egyenletek és egyenlőtlenségek megoldásában.

"Lecke logaritmikus funkciója" - öntanulás. Oldja meg az egyenlőtlenséget. 1. opció: 2. lehetőség: Az egyenlet megoldása: logaritmikus "vígjáték 2> 3". Borisz Slutsky. Mert mint a hab, a rímünk esik. A komédia az egyenlőtlenséggel kezdődik, vitathatatlanul helyes. Megismétlés és általánosítás lecke. A lecke epigráfusa: És a nagyság lépésről lépésre A logaritmusokba visszahúzódik.

Kapcsolódó cikkek

előző ◈ a következő