A funkcionális hézagok, szélsőségek, az online matematika előkészítésének monotonitásának vizsgálata
\ (\ blacktriangleright \) Az \ (f (x) \) függvény növekszik a \ (X \) intervallumon. ha bármilyen \ (x_1, x_2 \ in X \) esetén. úgy, hogy \ (x_1
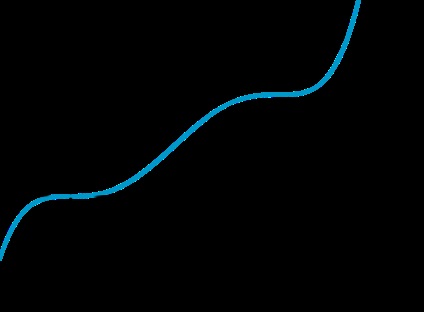
A függvényt a (\ \ \ \ \ \ \ \ \ \ \ intervallum \ \ \ intervallumon) nem kívánja megszüntetni. ha bármilyen \ (x_1, x_2 \ in X \) esetén. úgy, hogy \ (x_1
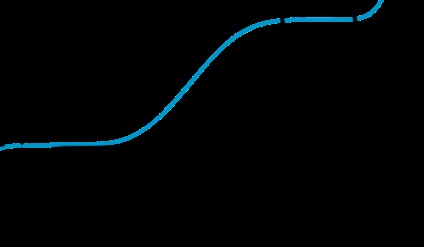
\ (\ blacktriangleright \) A \ (f (x) \) függvényt az \ (X \) intervallumon csökkenőnek nevezzük. ha bármilyen \ (x_1, x_2 \ in X \) esetén. úgy, hogy \ (x_1

A függvény neve nem növekszik a \ (X \) intervallumon. ha bármilyen \ (x_1, x_2 \ in X \) esetén. úgy, hogy \ (x_1

\ (\ blacktriangleright \) A növekvő és csökkenő funkciókat szigorúan monotonnak nevezzük. és nem növekvő és nem csökkenő - csak monoton.
\ (\ blacktriangleright \) Fő tulajdonságok:
I. Ha a \ (f (x) \) függvény szigorúan monoton a \ (X \). akkor az egyenlőség \ (x_1 = x_2 \) (\ (x_1, x_2 \ in X \)) \ (f (x_1) = f (x_2) \). és fordítva.
Például: a \ (f (x) = \ sqrt x \) függvény minden \ (x \ -ban [0; + \ infty] \) szigorúan növekszik. ezért az egyenlőség \ (\ sqrt x = \ sqrt 4 \) azt jelenti, hogy \ (x = 4 \).
II. Ha a \ (f (x) \) függvény szigorúan monoton a \ (X \). akkor a \ (f (x) = c1) egyenlet. ahol \ (c \) egy szám, mindig van egy megoldás a \ (X \) -on.
Például: az \ (x \ in (- \ infty; 0] \) függvény \ (f (x) = x ^ 2 \) szigorúan csökken, ezért a \ (x ^ 2 = 9 \ legfeljebb egy megoldás, vagy inkább egy: \ (x = -3 \).
a függvény \ (f (x) = - \ dfrac 1 \) minden \ (x \ in (-1; + \ infty) \) szigorúan növekszik. ezért a \ (- \ dfrac 1 = 0 \) egyenlet ezen az intervallumon nem több, mint egy megoldás, vagy pontosabban nem, mert. a bal oldali számláló soha nem lehet nulla.
III. Ha a \ (f (x) \) függvény nem kímél (nem növekszik) és folyamatos a \ ([a, b] \) intervallumon. és az intervallum végein az \ (f (a) = A, f (b) = B \) értékeket veszik. akkor \ (C \ in [A; B] \) (\ (C \ in [B; A] \)) az \ (f (x) = C \) egyenlet mindig legalább egy megoldást tartalmaz.
Például: \ (f (x) = x ^ 3 \) függvény szigorúan növekszik (azaz szigorúan monoton), és folyamatosan minden \ (x \ in \ mathbb \) függvényében. ezért minden \ (C \ in (- \ infty; + \ infty) \) egyenlet \ (x ^ 3 = C \) pontosan egy megoldást tartalmaz: \ (x = \ sqrt [3] \).
A (z \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ax \ balra, és tartalmazza \ (x ^ 2 \) - jobbra, és fontolja meg a függvényt
\ f (t) = 5 (t-2) ^ 3 + 15e ^ t + 6e ^ t \ cdot \ sin + 3e ^ t \ cdot \ cos \]
Ezután a kezdeti egyenlet a következő alakú:
\ [f (ax) = f (x ^ 2) \]
Találjuk meg a származékot:
\ (f) (t) = 15 (t-2) ^ 2 + 15e ^ t \ cdot (1+ \ cos) \]
mert \ ((t-2) ^ 2 \ geqslant 0, \ e ^ t> 0, \ 1 + \ cos \ geqslant 0 \). akkor \ (f '(t) \ geqslant 0 \) minden \ (t \ in \ mathbb \) esetén.
Továbbá \ (f '(t) = 0 \). ha \ ((t-2) ^ 2 = 0 \) és \ (1 + \ cos = 0 \) ugyanabban az időben, amely nem áll fenn semmilyen \ (t \) esetén. Következésképpen \ (f '(t)> 0 \) bármilyen \ (t \ in \ mathbb \) esetén.
Így a \ (f (t) \) függvény minden egyes \ (t \ in \ mathbb \) szigorúan növekszik.
Ezért az \ (f (ax) = f (x ^ 2) \) egyenlet egyenértékű az \ (ax = x ^ 2 \) egyenletével.
A \ (a = 0 \) egyenlet \ (x ^ 2-ax = 0 \) egy gyökér \ (x = 0 \). és \ (a \ ne 0 \) két különböző gyökérből áll: \ (x_1 = 0 \) és \ (x_2 = a \).
Ezért a válasz: \ (a \ in (- \ infty; 0) \ cup (0; + \ infty) \).
Hozzárendelési szint: Raven EGE
Keresse meg a \ (a \) paraméter összes értékét. amelyek mindegyikére a \ [2 ^> \ cdot \ log _ >> + \ log_9 + 2)> = 0 \] egyenlet
egyedülálló megoldást kínál.
Hozzárendelés hozzáadása a kedvencekhez
Tekintsük az \ (y = 2 ^ t \ cdot \ log _> \), amikor \ (t \ geqslant 0 \) (például a \ (\ sqrt \ geqslant 0 \)).
A derivált \ (y '= \ left (-2 ^ t \ cdot \ log_9 \ right)' = - \ dfrac \ cdot \ left (\ ln 2 \ cdot \ ln + \ dfrac \ jobb) \).
mert \ (2 ^ t> 0, \ \ dfrac> 0, \ \ ln> 0 \) minden \ (t \ geqslant 0 \) számára. akkor \ (y '<0\) при всех \(t\geqslant 0\).
Következésképpen \ (t \ geqslant 0 \) a \ (y \) függvény monoton módon csökken.
Az egyenlet formája \ (y (t) = y (z) \) formájában tekinthető. ahol \ (z = ax, t = \ sqrt \). A függvény monotonitásából az egyenlőség csak akkor lehetséges, ha \ (t = z \).
Ezért az egyenlet ekvivalens az egyenlettel: \ (ax = \ sqrt \). amely viszont egyenértékű a rendszerrel: \ [\ begin a ^ 2x ^ 2-x-1 = 0 \\ ax \ geqslant 0 \ end \]
A \ (a = 0 \) esetében a rendszernek van egy megoldása \ (x = -1 \). amely megfelel a \ (ax \ geqslant 0 \) feltételnek.
Az ügyet \ (a \ ne 0 \) tekintjük. A \ (D = 1 + 4a ^ 2> 0 \) rendszer első egyenletének diszkriminansa minden \ (a \) számára. Következésképpen az egyenletnek mindig két gyökere van \ (x_1 \) és \ (x_2 \). és ezek különböző jelek (mert Viet tétele \ (x_1 \ cdot x_2 = - \ dfrac<0\) ).
Ez azt jelenti, hogy \ (a<0\) условию \(ax\geqslant 0\) подходит отрицательный корень, при \(a>0 \) egy pozitív gyökér alkalmas. Ennek következtében a rendszer mindig egyedi megoldást kínál.
Ezért \ (a \ in \ mathbb \).
Vegyük figyelembe a \ (a \) függvény \ (f (x) = 2x ^ 3-3x (ax + x-a ^ 2-1) -3a-a ^ 3 \) függvényt. Lássuk a következő deriváltjait: \ (f '(x) = 6x ^ 2-6ax-6x + 3a ^ 2 + 3 = 3 (x ^ 2-2ax + a ^ 2 + x ^ 2-2x + 1) = 3 xa) ^ 2 + (x-1) ^ 2) \).
Vegye figyelembe, hogy \ (f '(x) \ geqslant 0 \) minden \ (x \) és \ (a \) értékre. ahol \ (0 \) egyenlő csak \ (x = a = 1 \). De \ (a = 1 \):
\ (2 (x-1) ^ 3 = 0 \) egyenlet \ (f '(x) = 6 (x-1) ^ 2 \ Rightarrow f (x) = 2 (x-1) ^ 3 \ egy egyedi root \ (x = 1 \). amely nem felel meg a feltételnek. Ezért \ (a \) nem egyenlő lehet \ (1 \).
Ennélfogva, az összes \ (a \ ne 1 \) függvény \ (f (x) \) egy szigorúan növekvő, tehát, az egyenlet \ (f (x) = 0 \) lehet legfeljebb egy gyökér. Figyelembe véve a köbös függvény tulajdonságait, a \ (f (x) \) grafikon néhány rögzített \ (a \) esetében így fog kinézni:

Ez azt jelenti, hogy az egyenletnek gyökere van a \ ([- 1; 0] \) intervallumban. kell lennie: \ [\ kezdődik f (0) \ geqslant 0 \\ f (-1) \ leqslant 0 \ end \ Rightarrow \ kezdődik egy (a ^ 2 + 3) \ leqslant 0 \\ (a + 2) (a ^ 2 + a + 4) \ geqslant 0 \ end \ Rightarrow \ kezdődik egy \ leqslant 0 \\ a \ geqslant -2 \ end \ Rightarrow -2 \ leqslant egy \ leqslant 0 \]
Így \ (a \ in [-2; 0] \).
Hozzárendelési szint: Raven EGE
Keresse meg a \ (a \) paraméter összes értékét. (\ sin x-3) + 6) \ cdot (\ sqrt2a + 8x \ sqrt) = 0 \] az egyenletet \ [(\ sin ^ 2x-5 \ sin x-2a
(Feladat felkérése)
Hozzárendelés hozzáadása a kedvencekhez
Az ODZ egyenlet: \ (2x-2x ^ 2 \ geqslant 0 \ quad \ Leftrightarrow \ quad x \ a [0; 1] \). Ezért, annak érdekében, hogy az egyenlet volt egy gyökér, az szükséges, hogy legalább az egyik az egyenletek \ [\ sin ^ 2x-5 \ sin x-2a (\ sin x-3) + 6 = 0 \ quad >> \ quad \ sqrt2a + 8x \ sqrt = 0 \] volt megoldás a DSB-n.
1) Tekintsük az első egyenletet \ [\ sin ^ 2x-5 \ sin x-2a (\ sin x-3) + 6 = 0 \ quad \ Leftrightarrow \ quad \ left [\ begin \ begin \ sin x = 2a + 2 \\ \ sin x = 3 \\ \ end \ end \ jobb. \ quad \ Leftrightarrow \ quad \ sin x = 2a + 2 \] Ennek az egyenletnek gyökerekkel kell rendelkeznie \ ([0; 1] \). Tekintsük a kört:
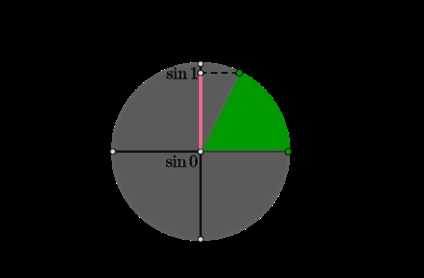
Így láthatjuk, hogy minden \ (2a + 2 \ in [\ sin 0; \ sin 1] \) esetében az egyenletnek van egy megoldása, de minden más számára - ez nem lesz megoldás. Következésképpen, az \ (a \ in \ left [-1; -1 + \ sin 1 \ jobb] \) az egyenlet megoldásokkal rendelkezik.
2) Tekintsük a következő egyenletet: \ [\ sqrt2a + 8x \ sqrt = 0 \ quad \ Leftrightarrow \ quad 8x \ sqrt = -a \]
Tekintsük a \ (f (x) = 8x \ sqrt \) függvényt. Azt találjuk, annak származéka: \ [f „(x) = - 4 \ cdot \ dfrac> \] A TCC van egy nulla-származék: \ (x = \ frac34 \). amely szintén a \ (f (x) \) függvény maximális pontja.
Megjegyezzük, hogy \ (f (0) = f (1) = 0 \). Ez azt jelenti, hogy az \ (f (x) \) grafikon vázlatos:
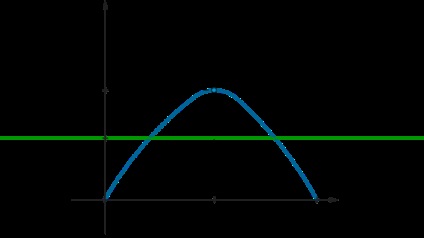
Ezért annak érdekében, hogy az egyenlet megoldásokkal rendelkezzen, szükséges, hogy az \ (f (x) \) grafikon metszi a \ (y = -a \) sorral (az ábrán az egyik megfelelő opció látható). Ez azt jelenti, meg kell, hogy \ [0 \ leqslant -a \ leqslant f \ left (\ dfrac34 \ right) \ quad \ Rightarrow \ quad - \ dfrac2 \ leqslant a \ leqslant 0 \]
3) Így a kezdeti egyenlet megoldásokat fog találni a \ (a \ in \ balra [-1; -1 + \ sin 1 \ jobb] \) vagy \ (a \ in \ left [- \ dfrac2; 0 \ right] \). Ezen megoldások kombinálásával \ [a \ in \ left [- \ dfrac2; 0 \ right] kapunk. \]
Funkciók családjait \ (f_a (x) = \ sqrt + 5x ^ 2-9x + 3a + 8, \ \ g_a (x) = \ dfrac \) tekintjük.
Az egyenlet ODZ-je: \ (x \ geqslant 1 \). Ezekhez a \ (x \):
A függvény \ (y_1 = \ sqrt \) szigorúan növekszik. A \ (y_2 = 5x ^ 2-9x \) függvény egy olyan parabola, amelynek csúcspontja a \ (x = \ dfrac \) pontban van. Következésképpen minden \ (x \ geqslant 1 \) függvény (\ y_2 \) szintén szigorúan növekszik (a parabola jobb oldala). mert a szigorúan növekvő függvények összege szigorúan növekszik, majd \ (f_a (x) \) szigorúan növekszik (az állandó \ (3a + δ \) nem befolyásolja a függvény monotonitását).
A \ (x \ geqslant 1 \) függvény \ (g_a (x) = \ dfrac \) a hiperbola jobb ágának része, és szigorúan csökken.
Az \ (f_a (x) = g_a (x) \) egyenlet megoldása - a \ (f \) és \ (g \) függvények metszéspontjainak megtalálása. Ellenkező monotonitásukból következik, hogy az egyenletnek nem lehet több gyökere.
A \ (x \ geqslant 1 \) \ (f_a (x) \ geqslant 3a + 4, \ \ \ 0
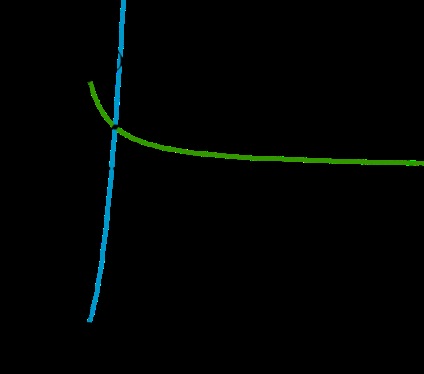
\ [3a + 4 \ leqslant a ^ 2 \ Rightarrow a \ in (- \ infty; -1] \ cup [4; + \ infty] \]