Számítsd ki a pi számot
A számítási módszer a következő ötleten alapul:
- Egy körsugárral ellátott kör a második oldalon lévő négyzetbe van beírva.
- Véletlen pont koordinátáit képezzük (homokot vetünk egy adott négyzetbe, egy kavicsba). Ez a véletlenszerű "dobás" és a kapcsolódó módszer a tőke a szerencsejáték, ahol minden is épült véletlenszerű.
- Egy pont körbe eshet vagy nem (a találati feltétel: x 2 + y 2 <= 1)
- Az Np-k számát a megfelelő számú N dobásra számítjuk.
- Ha a pontok véletlenszerűek, akkor a megtalált pontok aránya a kísérletek számához viszonyítva egyenlő a kör és a négyzet területének arányával. Np / N = Scr / Sqn = πR2 / (2R) 2
- A szám π = 4 · Np / N
A "tiszta" Pascal program így néz ki:
A számítás pontossága a próbálkozások számától függ (n szám).
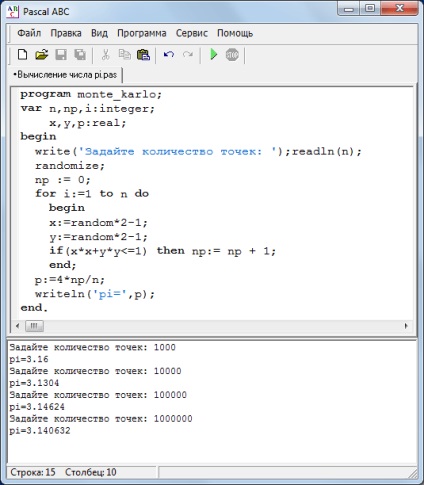
a pi szám kiszámítása egy másik számú kísérlethez
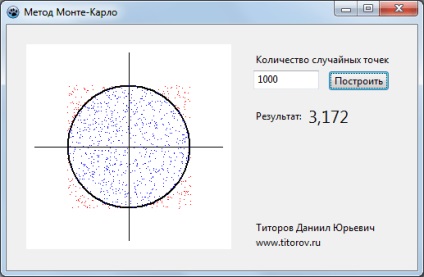
A Lazarus vizuális részének megvalósításához a véletlenszerű Descartes-koordinátákat át kell alakítani a képernyő-koordinátákra, akárcsak a cikkben: Grafikus funkció létrehozása Lasarusban. Az alkalmazás tartalmaz egy TImage komponenst egy kép, egy beviteli mező, egy gomb és több címke felépítésére:
Az x, y koordinátákhoz tartozó véletlen pont (a (-1; 1) tartományban lévő valós számok le vannak fordítva a képernyő koordinátáira:
xd: = kerek (x0 + x * r);
yd: = kerek (y0 + y * r);
ahol r egy szegmens képpont hosszúsága.
A pontot a következő módszerrel festettük: Form1.image1.Canvas.Pixels [xd, yd]: = clBlue;
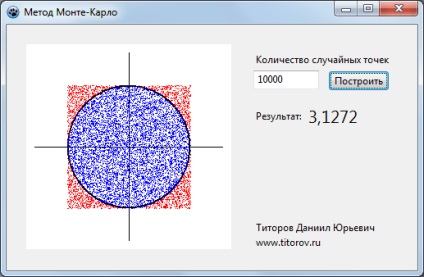
10 000 véletlen pont. A számítás pontossága magasabb.
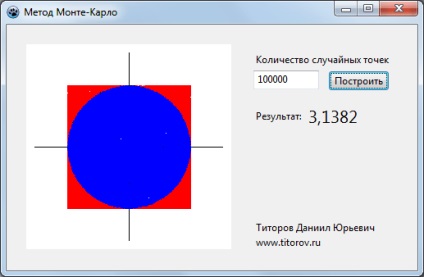
Könnyen megtekinthető az elérni kívánt pontosság csak elég nagy számú felvétel esetén. A pontosságot a véletlenszám-generátor minősége határozza meg.