Spline modellek építése
PostroenieSplinemodeley.
Számos interpolációs csomópontnál az interpolációs polinomok mértéke erőteljesen növekszik, ami számításokhoz kényelmetlenül teszi őket. A polinomok nagyfokú fokozatossága elkerülhető úgy, hogy az interpolációs szegmenst több részre osztja, az interpolációs polinom egyes részeiben. Ezt a módszert spline interpolációnak nevezzük. A legáltalánosabb az egyes szakaszokon végzett konstrukció [xi. xi + 1], i = 0..n-1 a köbös függvény.
A spline egy töredék polinomiális függvény. A részleges szegmensek mindegyikénél a köbös spline [xi. xi + 1] formája a következő lesz:
ahol az ismeretlen koefficienseket úgy választjuk meg, hogy az interpoláló spline-ek ugyanolyan első és második sorrendű származékokat kapjanak a térhálósító pontokban.
Az u együtthatók meghatározásához az alábbi egyenleteket kaphatjuk:
1. Az interpolált függvény értékeinek és a csomóponti pontokon lévő spline értékek egyenlőségének feltételei
2. Varrás az első spline-származékok elemi intervallumainak határán
3. Varrás a második spline-származékok elemi intervallumainak határán
4. A "szabad varrás megerősítése"
; ;
Ezeknek a feltételeknek és egy köbös spline-nek a használata az alábbi egyenletrendszerhez vezet:
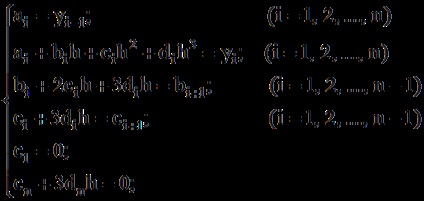
Hol van a szomszédos pontok közötti távolság (x lépés).
A köbös spline együtthatóinak meghatározására szolgáló algoritmus:
1. Az együtthatók meghatározása:
2. Az együtthatók mátrixának és az SLAU szabad tagjai vektorának kialakítása
- a fő átlós elemek
- oldalátló elemei
- a szabad kifejezések vektorának komponensei
3. Az SLAU döntése a következőkről:
És egy együtthatós tömb hozzáadása egy elemhez
4. Az együtthatók kiszámítása
5. Az együtthatók kiszámítása
Egydimenziós spline modellek építése:
Ebben a munkában az érzékelő modellező programot alkalmaztuk a kimenő jel hőmérséklettől és nyomástól való függőségének szimulálására (1. ábra):
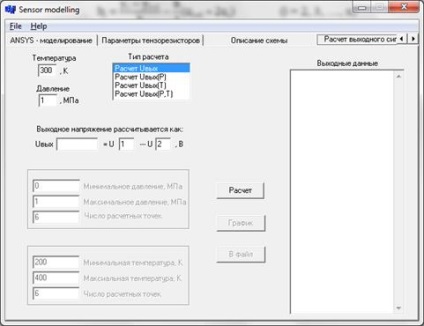
Ábra. 1. A használt program.
A program segítségével kiszámoltuk és rajzoltuk a kimeneti jel hőmérsékletfüggését (2. ábra):

Ábra. 2. A kimeneti jel függése a programban kapott hőmérséklet függvényében Érzékelő modellezés.
Az egydimenziós spline modell megszerzéséhez:
1. Az alprogramokat tartalmazó Spline.cpp modul:
- SplineCoeff - egy táblázatos funkciójú köbös spline együtthatóinak kiszámítása.
- LineProgon - SLAU megoldás sweep módszerrel
- Spline - egy adott függvény függvényének spline interpolációján alapuló értékeinek kiszámítása
- SdxSpline - a táblázat függvény integráljának kiszámítása az adott korlátokban a spline interpoláció alapján.
2. A spline funkció szimuláló SPL1_001.cpp program
3. Graphic2.cpp program a függvénygrafikon kiszámításához.
Ennek eredményeként ezeknek a programoknak a használatát a spline funkcióval lehet elérni:
dupla s (dupla x)