Információs oldal a
Numerológia, pszeudosciáció, matematika, a számok numerikus csökkentésének képletét és számológépeit
AM Belov
Számmisztika - rendszerek, hagyományok és hiedelmek a misztikus vagy ezoterikus kapcsolat a szám és a fizikai tárgyak vagy élőlények és a tudatuk. Ezért is nevezik mágikus számok, de közel van a koncepció az asztrológia és a többi parascience ókorban. Számmisztika és jóslás számmisztikai körében népszerűek voltak a korai matematikusok, mint például a pythagoreusoknál és nem tekinthetők jelenleg matematikai tudás, mint abban az esetben az elválasztás az alkímia, a kémia vagy a csillagászat asztrológia.
Végül pedig egészen egyszerűen azt mondják, hogy a numerológia egy pszeudosciáció a számokról.
Azok számára, akik nem egészen értem, magyarázza - áltudomány, ez egy ál-parascience, kvazinauka, alternatív tudomány, nem akadémiai tudomány, deviáns tudomány - vélt vagy hamis tudomány, az üzleti vagy oktatási, tudatosan vagy öntudatlanul utánozva a tudomány, de valójában azok, nem.
Együtt numerológia áltudomány jellemzően alkímia, asztrológia, szuperkritikus történetírás vagy „új időszámítás” hullám a genetika, a torziós mezők, parapszichológia, telepátia, telekinézis, pszichotronikus fegyverek, telepatikus, Telegonia, grafológia, valeology Dianetika szocionikusoknak, frenológiát, homeopátia és t. p.Samo saját összeállítás egy ilyen lista, hogy szükség van pontosan milyen kell tekinteni az áltudomány, általában rossz jel. Mivel ez azt jelzi, hogy még mindig nincsenek világos és egyértelmű kritériumok az igazi tudomány elválasztására. Ennek eredményeképpen hülye és abszurd állítások vannak. Például meg lehet találni azt a kijelentést, hogy a numerológia megtagadja a következtetéseinek megcáfolását. De a számmisztika nem személy, ami azt jelenti, hogy semmit sem tagadhat, sem megerősíthet. Ez megegyezik azzal, hogy megpróbálja bizonyítani, hogy egy szék az Ön számára, itt ott van valami. Miután egy ilyen igazi tudós, egy harcos ellen áltudomány, és a legtöbb biztonságosan lehet küldeni egy pszichiátriai kórházba.
Ez a rendszer, egy olyan formában, amelyet a modern nyugati és orosz számtani iskolák használnak. Főleg a jövőben fogunk beszélni róla.
A számok bizonyos mértékig tükrözik az objektumok, a jelenségek, a folyamatok egymás közötti viszonyát, kölcsönös befolyását egymásra. A számmisztikai szempontból idő múlásával a végtelenségig ismétlődő ciklusok 1-től 9 Természetesen az a tény, hogy ebben a világban minden mindennel összefügg jól ismert. A természetvédelmi törvények léte egyedül ezt erősen megerősíti. A másik kérdés az, hogy ez mennyire kölcsönös egymásra hatás, amennyire lehet részletes előrejelzést a fejlődés egy folyamat, mennyire megbízható lehet ez az előrejelzés, akkor lehet, hogy felmérjék egy adott objektum összege minden más tárgyak a környező világot.
Elméletileg meg lehet becsülni az egyetlen objektum numerológiai előrejelzésének lehetséges pontosságát a numerikus számok csökkentésének pusztán matematikai függvényével. Természetesen ez csak egy olyan rendszerre érvényes, amely csak két kölcsönösen befolyásoló objektumot tartalmaz. Mivel a rendszerben lévő tárgyak nőnek, az előrejelzés pontossága minden esetben növekedni fog.
Hasonlóképpen, ha a készítmény numerológiai előrejelzése figyelembe kell venni továbbá a például születési dátum, születési hely, születési idő, az életkor a szülők, és így tovább. D. A pontosság és informativitást számmisztikai előrejelzés emelkedik jelentősen.
És mégis, meg kell jegyezni, hogy mind az időjárás-előrejelzések, mind a számszerű előrejelzések esetében a 100% -os megbízhatóság még nem érhető el. A meteorológia azonban nem tekinthető pszeudo-tudománynak.
A számok számszerű csökkentésének matematikai függvényének megteremtése érdekében kívánatos, hogy a numerikus számok csökkentésével egyenlet (képlet) legyen. Mint tudják, még nincsenek ilyen szintek.
Létrehozhat egy olyan egyenletet, amely számos módon számolja a számok numerikus csökkentését. Például ezt teheti meg, ahogy azt mondják, "a homlokán", vagyis írja le a Pythagoras által javasolt számcsökkentés algoritmust egy képlet formájában. Ezután az (1) egyenletet kapjuk.
ahol x - az értéket, hogy csökkentsék a számát (a továbbiakban, az összes képlet ebben a cikkben); m az x számjegyszám; [] - aláírja jelöli egész részét, vagy működése eldobjuk törtrészének a számítás eredménye az expressziós a szögletes zárójelben (a továbbiakban, az összes képlet ebben a cikkben).
A matematika, találtuk az állítás, hogy a numerológiai számának csökkenése megegyezik a csere az eredeti számát a fennmaradó integer osztás 9. Ez azt jelenti, azt feltételezzük, hogy az eljárás számának csökkentése numerológiai leírható számtani módszereket levonás, amelyet gyakran nevezik moduláris aritmetikai vagy moduláris aritmetika. Ha ez így van, akkor a kívánt egyenletet nagyon egyszerű egyenlet formájában (2) írhatjuk.
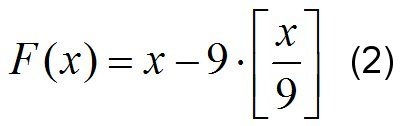
Ugyanaz az egyenlet általánosan írható, ha a 9-es számot az m modullal helyettesítjük (számszerûsítés céljából leggyakrabban az érték 9), amely elméletileg megegyezhet bármely természetes számmal:
A képlet végrehajtja azt az eljárást, hogy az eredeti számot a maradék részével az egész számosztástól az m modul helyettesítse. Meg kell jegyeznünk, hogy a maradékok aritmetikájában ezt az eljárást ismeretlen okokból előnyben részesítjük, hogy ne alakítsunk ki formulát, hanem verbális készítményekben. Talán a képlet alkalmazása lehetővé tenné a maradékanyag számtani alkalmazásának jobb megértését, és elkerülhető lenne számos téves állítás megjelenése.
Azonban örülni, hogy a matematikusok numerológusok számára egy egyszerű és kényelmes képletet számszerűsített számok csökkentése még mindig nem éri meg. Először a matematikai kimutatás kísérleti ellenőrzését végezzük. Egyébként a kísérleti teszt elvégzése az ál-tudomány egyik kritériuma. Következésképpen azonnal igazoljuk ezt a matematikai kijelentést és a pszeudosciát.
És így vesszük a 17-es szám, és vágjuk a szokásos elfogadott modern numerológia eljárás t. E. hozzá a szám 1 és 7 eredmény 8. Most, ossza 17 9, és meglátjuk, mi a további részében az osztás ugyanaz lesz 8-as szám . kiderül, hogy gondolkodunk egy matematikai állítás igaznak tűnik, de nem siet, és végezze el a másik kísérletben.
Most vesszük a szám 18 1 + 8 = 9, R. F. Numerologically száma 18 csökken 9. Most 18/9 = 2, m. E. 18 van osztva 9 maradék nélkül a fennmaradó vagy ezt a felosztást egyenlő 0, és nem 9-et, ahogyan azt a matematikai állítás szerint gondoljuk.
Az a tény, hogy a matematika pontosan az általános tudomány, általános és nagyon régi tévedés. Azt mondani, hogy a matematika pontos tudománya csak a külön szakaszok tekintetében lehetséges.
Annak ellenére, hogy mind a (2) egyenlet, mind a matematikai állítás, amely alapján összeállt, kiderült, hogy hibásak, mégis felhasználhatók a numerológiai szám redukciós egyenlet megszerzésére. Nyilvánvaló, hogy erre a célra a (2) egyenletet egyszerűen ki kell egészíteni olyan kifejezésekkel, amelyek lehetővé teszik, hogy a számítás során 0 legyen helyettesítve 9. Ennek eredményeképpen a numerikus számértékcsökkenés (3) egyenletének változatát kaphatjuk.
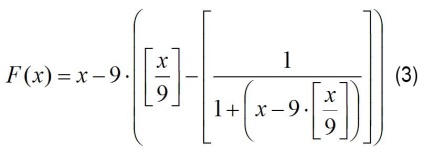
Ugyanez az egyenlet felírható általános formában helyettesítve száma 9 a modul m (numerológiát céljából leggyakrabban jelentése a - 9), amelynél elméletileg egyenlő bármely pozitív egész szám:
A (3) egyenlet segítségével elméletileg lehetséges bármely numerikus szám redukcióját 1-től a végtelenig. Azonban a (3) egyenlet alkalmazása során további verbális magyarázatok nem szükségesek. A szám a (3) egyenlet segítségével folyamatos számítások során csökken.
Ez a számológép természetesen nem képes nagyon nagy számok csökkentésére, hiszen minden számítógépen ismert a képességek korlátai. Gyakorlati használatra azonban nagyon alkalmas, mert az embernek általában nem kell nagyon nagy számokkal foglalkoznia.
A (3) egyenlet meghatározza a szám numerikus csökkentésének értékeinek változását a számváltozások értékeként. Nyilvánvaló, hogy ez a funkcionális függőség bonyolultabb, annál inkább elméletileg részletesebb és pontosabb számszerű előrejelzés érhető el. Az 1. ábrán. Az 1. ábra a számtani redukció függvény grafikonját mutatja, amelyet a (3) egyenlet felhasználásával alakítunk ki.
Ábra. 1 A numerikus számjegyek számának csökkentése 1-9-ig
A számmisztika azonban néha nem csak számokat, hanem számos karaktert is használ. A számszerű számítások egyes változataiban a kétszámjegyű 11-es és 22-es számokat dominánsnak is nevezik, és nem számolnak egyetlen számjegyre. Ismeretes az úgynevezett orosz számtudományi iskola, amely különbözik az összes többi számtani iskolától, mivel meghatározza a több mint 150 szám közvetlen jellemzőit. Ezért itt a 3. ábrán. A 2. ábra a numerikus számbavitel függvényének két számjegyű számsorra vonatkozó gráfja.

Ábra. 2 A számok numerikus csökkentésének funkciója egy kétjegyű számra
A két számjegyű számok számszerű csökkentésének funkcióját ábrázoló gráfot a (3) egyenlet felhasználásával állítottuk elő azáltal, hogy a m = 99 értéket helyettesítettük.
A 3. ábrán látható gráf. A 2. ábra bonyolultabb, mint a 3. ábrán. 1, de ennek ellenére, ha folytatja a formáját, akkor ne támaszkodjon a nagyon részletes és ugyanakkor pontos számszerű előrejelzésekre, valamint a kétszámjegyű számokra csökkentett számok alapján.
Ezért úgy tűnik, hogy a minőségi számszerűsített előrejelzések összeállítását számos befolyásoló tényező figyelembevételével kell elvégezni, amelyek mindegyike számával kifejezhető. Természetesen az ilyen számszerűsített előrejelzések összeállítása nagyon nehéz feladat, és a magasan képzett számológusok bevonását kell összefogniuk. A közeljövőben a több faktoros számszerű előrejelzések készítéséhez ugyanazt az eljárást hivatalosan is alátámasztani nem valószínű, hogy sikerülne.
A számmisztika művészetétől való erős függőség lehetővé fogja tenni számelméleti kritikáját a pszeudoscián elleni harcosoknak, de nem szabad megfeledkeznünk arról, hogy a holnapi logikus, ésszerű és megdönthetetlen holnapi pillanatok alatt nem fog kinézni. Minden a mi világunkban fejlődik és változik, az új hibák és pontatlanságok folyamatosan felmerülnek. Amelyek, nagyon jól tanúskodnak, a példák ebben a cikkben és hivatkozások példák más cikkek.