Mátrix meghatározók
Minden A négyzetes mátrix esetében bemutatjuk a | A | számot, amelyet meghatározónak nevezünk. Néha betűjelet is jelöl.
Ez a koncepció számos gyakorlati probléma megoldásához fontos. Határozza meg a számítási módszeren.
Az első rendű A mátrix esetében meghatározója az egyedüli eleme | A | = 1 = a11.
Egy másodrendű A mátrix esetében annak meghatározója egy olyan szám, amelyet az A | formula számít = 2 = a11 * a22-a21 * a12
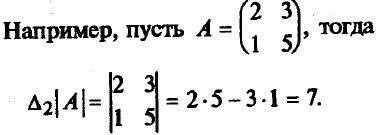
A harmadik rendű A mátrix esetében annak meghatározója egy szám, amelyet képlet alapján számítunk ki
Ez egy 6 algoritmusból álló algebrai összeg, amely mindegyik sorból pontosan egy elemet tartalmaz, és a mátrix minden oszlopát. A meghatározó képlet megjegyzése érdekében szokásos az úgynevezett háromszögek szabályozása vagy a Sarrus szabály (6.1. Ábra).

6.1 ábra - Háromszögek szabályozása
6.1 ábra, a baloldali ábrán látható, hogyan kell tételek kiválasztása szempontjából a „plusz” jel, - ezek a fő diagonális és a csúcsok egyenlő szárú háromszögek alapjai, amelyek párhuzamosan. A baloldali sémát a mínusz jelre használják; rajta a fő átló helyett az úgynevezett fedezet.
A magasabb megbízások meghatározóit rekurzív módon számítják ki, azaz a negyedik rend determinánsát a harmadik rend determinánsán keresztül, az ötödik rend determinánsát a negyedik rend determinánsa révén stb. Ennek a módszernek a leírásához be kell mutatni a mátrix elem kisebb és algebrai komplementjének fogalmát (rögtön megjegyezzük, hogy maga a módszer, amelyet az alábbiakban figyelembe veszünk, szintén alkalmas a harmadik és a második sor meghatározóira).
Az n-sorrendű mátrix aij elemének kisebb Mij az A mátrixból nyert (n-1) -rendű mátrix meghatározója az i-edik sor és a j-os oszlop törlésével.
Minden n-edik rend mátrix n 2 kiskorú (n-1) -rendben van.
Az n-edik rendezési mátrix aij elemének egy algebrai komplementje Aij a kisebb (-1) (i + j) jelű vonallal:
Az Aij = Mij meghatározásból következik. ha a sor- és oszlopszámok összege egyenletes, és Aij = -Mij. ha furcsa.
Például, ha
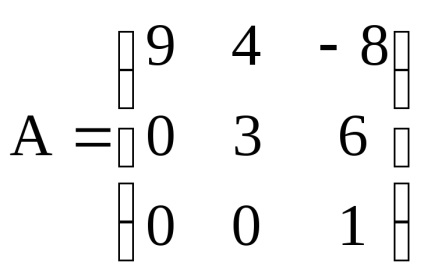
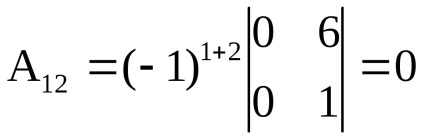
A determináns számítási módja a következő: a négyzetes mátrix meghatározója megegyezik bármelyik sor (oszlop) elemeinek termékeinek összegével az algebrai kiegészítésekkel:
(az i-es vonal elemeinek kitágulása;
(a j. oszlop elemeinek kitágítása;
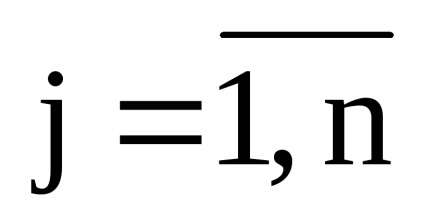

Megjegyezzük, hogy általánosságban a háromszög mátrix meghatározója megegyezik a fő átló elemeinek termékeivel.
Fogalmazzuk meg a determinánsok alapvető tulajdonságait.
1. Ha a mátrix bármely sorában vagy oszlopában csak nullák vannak, akkor a determináns 0 (a számítási módszerből következik).
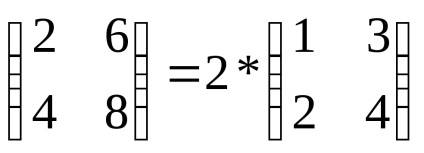
2. Ha minden eleme bármely sor (oszlop) a mátrix megszorozzuk az azonos számú, akkor annak meghatározó szorozni ezt a számot (az alábbiak szerint a számítási módszer - a számítás a kofaktorok közös tényező nem befolyásolja, és az összes többi kifejezéseket szorozni ez a szám).
Megjegyzés: a determináns jele számára lehetséges, hogy csak a sor vagy oszlop közös tényezője legyen (ellentétben a mátrixgal, amelynek jelét az összes elem közös tényezőjének figyelembe vétele). Például, de
3. Amikor a mátrix átültetésre kerül, annak meghatározója nem változik: | A | T | = | A | (nem kell elvégeznünk a bizonyítékot).
4. Ha egy mátrix két sorát (oszlopát) váltják egymással, meghatározó változásai az ellenkezőjére utalnak.
Ezt a tulajdonságot bizonyítva először azt feltételezzük, hogy a mátrix két szomszédos sorát átrendezzük: az i-th és (i + 1) -th. A számítás a meghatározó az eredeti mátrix megvalósítható bomlása i-edik sorának, és a meghatározó az új mátrix (sor-permutált) - a (i + 1) -edik (azaz ez ugyanaz, azaz, elemenként Match). Ezután a számítás a második meghatározó, minden egyes algebrai kívül lesz ellentétes előjelű, mint a (-1) épül nem a mértéke a (i + j), és a mértéke a (i + 1 + j), de egyébként nem fog különbözni képlet. Így a determináns jele az ellenkezőjére változik.
Most feltételezzük, hogy nem szomszédos, hanem két tetszőleges vonal átrendeződik, például az i-th és (i + t) -th. Ezt permutációs ábrázolható például szekvenciális smescheniei natstrok edik sor lefelé, és a (i + t) -edik sor - a (t-1) vonalak fel 1. Ez meg fogja változtatni a jele a meghatározó (t + t-1) = 2t- száma 1 idő, azaz. páratlan számú alkalommal. Következésképpen a végén meg fog fordulni.
Hasonló érvelést lehet megváltoztatni az oszlopokra.
5. Ha a mátrix két azonos sorozatot (oszlopot) tartalmaz, akkor meghatározója 0.
Valójában, ha ugyanazokat a sorokat (oszlopokat) átrendezzük, akkor ugyanazt a mátrixot kapjuk meg, azonos determinánsokkal. Másrészt az előző tulajdonság szerint meg kell változtatnia a jelet, azaz = -at = 0.
6. Ha a mátrix két sorának (oszlopainak) elemei arányosak, akkor a determináns 0.
Ez a tulajdonság alapján az előző tulajdonság és figyelmen kívül hagyva a közös tényező konzolt (eltávolítása után zárójelben arányossági együttható mátrix ugyanaz lesz a sorok és oszlopok, és ennek eredményeként, ez a tényező lesz szorozva nulla).
7. A mátrix minden sorának (oszlopának) elemeinek összege ugyanazon mátrix egy sorának (oszlopa) elemeinek algebrai komplementuma által mindig 0:
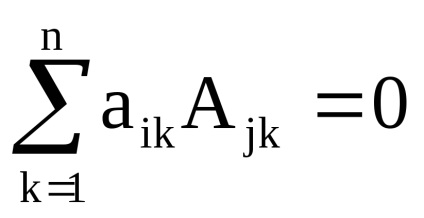
Ennek a tulajdonságnak a bizonyításához elegendő a j-es sor helyettesítése az i-th-vel az A. mátrixban. Az így kapott mátrixban két azonos sor lesz, tehát a meghatározója 0. Másrészt a j-sor elemeinek kibővítésével számítható ki:
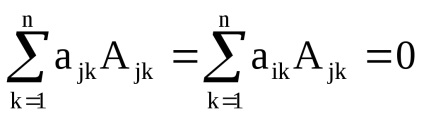
8. A mátrix meghatározója nem változik a mátrix sorának vagy oszlopának elemeihez, ha más sor (oszlop) elemeit hozzá kell adni azonos számhoz.
Tény, hogy az i-edik sor elemeihez hozzá kell adni a j-sor vonalának elemeit, amit meg kell szorozni a приба-val. Ezután az új i-edik sor elemei a forma (aik + ajk, akbank). Az új mátrix meghatározóját kiszámítjuk az i. Sor elemeiben történő bővítéssel (vegyük észre, hogy az elemeinek algebrai kiegészítései ebben az esetben nem változnak):
Megállapítottuk, hogy ez a meghatározó nem különbözik az eredeti mátrix meghatározójától.
9. A mátrixok termékének meghatározója megegyezik determinánsaik termékeivel: | AB | = | A | * | In | | (nem kell elvégeznünk a bizonyítékot).
A fentiekben megfontolt determinánsok tulajdonságait a számítás egyszerűsítésére használják. Általában megpróbálják átalakítani a mátrixot olyan formában, hogy bármelyik oszlop vagy sor tartalmazza a lehető legtöbb nullát. Ezt követően a determináns könnyen megtalálható a sor vagy oszlop bővítésével.


