Előfeszítési együtthatók kijelölése
A fogaskerekek vágásához
Az előfeszítési együtthatók a következőkhöz vannak rendelve:
- növelje a fog hajlítószilárdságát azáltal, hogy növeli veszélyes szakaszát az alap közelében;
- a fogak érintkezési szilárdságának növelése olyan köralakú szakaszok használatával, amelyek távolabb vannak a főkörön;
- a maximális specifikus csúszás igazítása;
- meg kell akadályozni, hogy a kis kerék alul legyenek a sebességváltóban;
- a továbbítás simaságának növelése az aktív vonal meghosszabbításával;
- adott interaxle távolság biztosítása;
- kétpólusú felszerelés biztosítása a póluson és egyéb célokra.
A fogaskerék geometriai méreteinek kiszámítása
A méretek kiszámításához a kezdeti adatok a következők: a kerekek fogainak száma és. kerék modul. az eredeti kontúr profiljának szöge. elmozdulási együtthatók és. a fogfej magasságának együtthatója és a radiális clearance együtthatója.
Az összefonódás szögének meghatározására szolgáló képletet itt a következtetés nélkül adjuk meg, annak tömege miatt
Ebből a képletből különösen látható, hogy a nulla fokozatban az összekapcsolási szög megegyezik a szerszám profilszögével. pozitív transzferben. a negatív átvitel során minden megfordult, azaz és /.
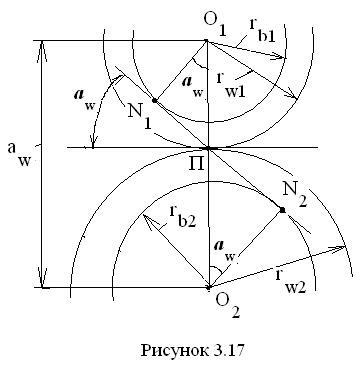
A képletek kivezetése céljából a 3. ábrához fordulunk. 3.17, amely bemutatja az elkötelezettség szükséges elemeit. Az N1 N2 összekötő vonal az összekapcsolási szöget alkotja # 945; w egy közös tangens a kezdeti körök a sugarak és. egymáshoz viszonyítva a póluson # 928;. Az O1 és O2 kerekek középpontjaihoz képest a merőlegesek leeresztése a hálóba, két derékszögű N1 O1 P és N2 O2 П háromszöget kapunk az O1 és O2 csúcsok sarkánál. egyenlő # 945; A háromszögből következik az N1 O1 P. az N2 O2 П- háromszögből. Mivel vannak egyenlők. . és. valamint. . akkor megkapjuk és. A körök eloszlásának és a fenti képleteknek helyett a korábban írt kifejezéseket is beilleszthetjük
Amint az az ábrából látható, az interaxiális távolság megegyezik a kezdeti körök sugarainak összegével, azaz. ezért
Az első két kifejezés terméke ebben a képletben az osztható interaxiális távolságnak nevezhető. Ez akkor fordul elő, ha az átvitel nulla, vagyis amikor a teljes elmozdulási együttható nulla. Ebben az esetben. és a koszinuszok csökken.