A pont és a test kinematikájának fő feladata
A pont kinematikájának fő feladata olyan módszerek kidolgozása, amelyek meghatározzák a mozgáspontot és a mozgás alapvető kinematikai jellemzőinek meghatározására szolgáló módszereket.
A szilárd test kinematikájának fő feladata olyan mozgási módszerek kidolgozása, amelyek lehetővé teszik számunkra, hogy az egyes pontok közös jellemzőinek kis számán alapulva megtaláljuk a test minden egyes pontjának kinematikai jellemzőit.
A pontok mozgásának meghatározása olyan matematikai berendezés kijelzésére, amelynek segítségével bármelyik adott időpontban meghatározható egy pont helyzete a térben.
3. Vektor, koordináta és természetes módon határozza meg a pont mozgását
Egy pont mozgásának meghatározása egy olyan matematikai berendezés meghatározásához, amelynek segítségével az adott időponthoz egy adott pont helyének meghatározása lehetséges.
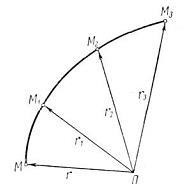
Az idő múlásával a pont megváltoztatja helyzetét a referenciatest térében. Ezért a sugárvektor mind irányában, mind nagyságrendjében változik, és a skaláris argumentum bizonyos vektorfüggvénye. . Ha a függvény meghatározott vagy ismert, akkor vektor módszer egy pont meghatározására.
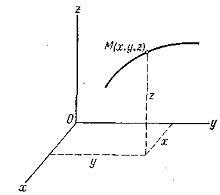
Ha a függvények ismertek vagy meghatározottak, akkor a mozgás meghatározására szolgáló koordináta-módszerről beszélünk.
Tájékoztassa velünk a pont pályáját. Ezen a pályán tetszőleges O pontot választunk. Az M pont helyzetét a pályán lehet megadni az ív koordinátával.
Az idők folyamán az ív koordinátája megváltozik, és egy bizonyos funkciót képvisel. Ha a függvényt megadjuk, egy pont mozgásának természetes meghatározására gondolunk.
4. A sebesség és a gyorsulás meghatározása a vektor mozgás módjában.
A mozgás meghatározására szolgáló vektor módszerrel a mozgási pont helyzetét az idő minden egyes pillanatában az idő függvényében lévő sugárvektor határozza meg, és amikor a pont mozgásban van, a sugárvektor növekményt kap. Az elmozdulásvektor aránya az időintervallumhoz. amely alatt ez a mozgás történik, a pont átlagos sebességének vektorja :.
Egy adott időben egy pont sebességvektora megegyezik a pont sugárvektorának származékával az idő függvényében:
A pont sebességsebessége a pályán a pont mozgásának irányában érintkezik.
Tegyük fel, hogy az első pillanatban a pontnak van egy sebessége. és egy idő után növekszik. A növekményt időintervallummal osztva. ezen időtartam alatt kapjuk meg a pont átlagos gyorsulásának vektorát. A pont gyorsulási vektora megegyezik a sebesség első deriváltjával vagy a pont időbeli sugárvektorának második származékával.
A gyorsító vektor a mozgási pont sebességvektorainak végpontjainak geometriai helyére irányul, amelyet ugyanazon tetszőleges térbeli helyről helyeznek el.
5. A sebesség és a gyorsulás meghatározása a pont mozgásának meghatározására szolgáló koordináta-módszerrel
Adjuk meg a pont mozgásának egyenleteit:
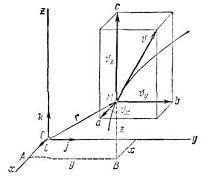
Kiszámítása után a nyúlványok a sebesség tengelyére derékszögű koordináták, lehetséges meghatározni a nagyságát és irányát a sebesség vektor a következő képletekkel:
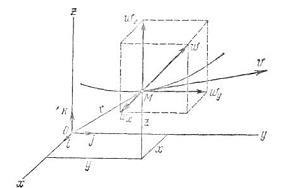
A gyorsulás vetületének kiszámítása a koordináta-tengelyeken meghatározhatjuk a gyorsulás modulusát és irányát a következő képletek szerint:
6. A sebesség és a gyorsulás meghatározása természetes ponton egy pont mozgásának meghatározására
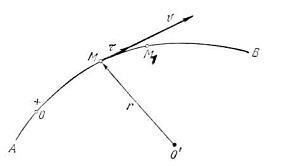
Elfogadjuk, hogy a szimbólummal jelöljük a sebesség algebrai értékét. és a sebességmodul egy betű. majd:
azaz a sebesség modulus megegyezik a pont ív koordináta származékának abszolút értékével az időhöz viszonyítva.
A pont gyorsulásának vetülete az érintőn megegyezik az idő pontjának ív koordináta második deriválásával, vagy a pont sebességének algebrai értékének első deriváltjával az idő függvényében.
A test progresszív mozgása. Állítsa be a mozgást. A testpontok sebességének és gyorsulásának megoszlása
A merev test progresszív mozgása olyan mozgás, amelyben a test két pontját összekötő egyenes vonal párhuzamosan mozog.
Tétel. A merev test transzlációs mozgást végző pontjai ugyanazokat a pályákat írják le (amelyek egybeesnek az átfedéssel), és minden időpontban geometriailag egyenlő sebességek és gyorsulások vannak.
A merev test transzlációs mozgásának egyenletei a test bármelyik pontjának mozgásának egyenletei - általában a súlypont mozgásának egyenletei:
A merev test transzlációs mozgásának gyorsasága és gyorsulása a gyorsulás gyorsaságát jelenti egy szilárd test transzlációs mozgásának minden pontján.
Forgó mozgás. Állítsa be a mozgást
A forgatás egy olyan test mozgása, amelyben minden pontja állandó marad, egyenes vonallal, amely a forgás tengelye.
Ebben a mozgásban a test minden más pontja mozgásban van a forgástengelyre merőleges síkokban, és leírja azokat a köröket, amelyeknek központja ezen a tengelyen fekszik.
Amikor a test forog, a forgásszög idővel változik :.
A forgásszög változásának gyorsaságát jellemzo nagyságrendet a test szögsebességének nevezik.
A szögsebesség változásának sebességét jellemzo nagyságát a test szögsebességének nevezik.
A test egyenletes elfordulási egyenlete. Egy állandó sebességű test forgatását egységesnek nevezzük.
A test egyenletes elfordulási egyenlete. A test forgatását, amelyben a szögsebesség állandó, a váltakozó forgásnak nevezzük.