A kinematikában az elméleti mechanikában egy probléma megoldásának egyik példája a sebesség, a gyorsulás, a szám keresése

állapot:
A szögelfordulás ε = 2 rad / s egyenletes gyorsulással elforgatott testének t1 = 2,5 c szögsebessége ω1 = 40 rad / s.

Határozza meg a következőket: 1) a test pontjának gyorsasága és gyorsulása h = 55 cm-re a t2 = 7 s időtartamú forgástengelytől; 2) a test N fordulatszámának száma t3 = 10 c; a test rotációs mozgásának egyenlete, ha a kezdeti időpontban t0 = 0 a kezdeti forgási szög φ0 = 0.

megoldás:
1. Egyenesen felgyorsított forgatással a test szögsebessége a törvénynek megfelelően változik

Annak tudomásul vételével, hogy a szögsebesség ω1 értéke egy bizonyos időpontban t1 és az α szögsebességgel megegyezik, akkor az ω0 kezdeti szögsebességet t0 = 0:

Ezért a test szögsebessége a t2 = 7 s idő alatt megegyezik

A v sebesség és a test M pontjának a gyorsulása h = 55 cm-re a forgási tengelytől a t2 = 7 s időpontban megegyezik:

v = ω2 · h = 49 · 55 = 2695 cm / s = 26,95 m / s;
αvr = ε · h = 2 · 55 = 110 cm / s 2 = 1,10 m / s 2;
αο = ω 2 · h = 49 2 · 55 = 132055 cm / s 2 = 1320,6 m / s 2;

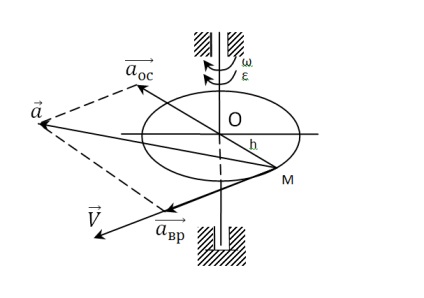
A sebesség és a gyorsulás vektorok irányát az ábrán a feladat jelzi.

A testforgatások számát a t3 = 10 c időtartam alatt a reláció határozza meg

ahol n (t) a testfordulatszám másodpercenként egy adott időpontban.

A probléma, amit mérlegelünk

A φ = φ (t) test rotációs mozgásának egyenletét a (T) = dφ / dt => dφ = ω (t) · dt relációból kapjuk meg. A differenciálegyenletet a kezdeti feltételekhez (t0 = 0, φ0 = 0) integráljuk:

A kinematikai elméleti mechanika problémájának megoldása befejeződött.

Tisztelettel, Site Administrator.