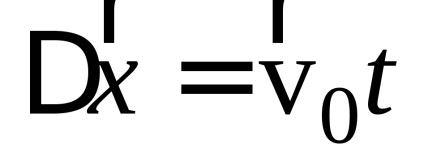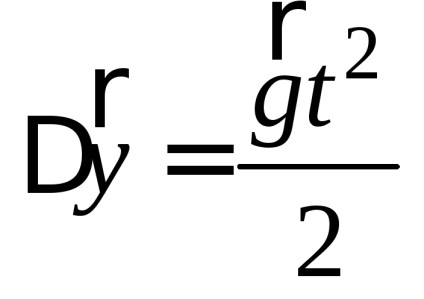A testek szabad mozgása a horizonton szöget bezárva a problémák megoldásának példái
1. A testet a Föld felszínéről egy szögben = 60 ° a látóhatárhoz vetettük, kiindulási sebesség v0 = 20 m / s. Figyelmen kívül hagyva a levegő ellenállását:
a) a test sebességét a mozgás kezdete után t = 2 s után;
b) a t1 időpontot. amelyen keresztül a fordulatszám a horizonton lesz: angle = 30 °;
c) a T test elhagyásának ideje, mielőtt a Földre esne;
d) a H maximális emelési magasság és az L repülési tartomány;
e) az y (x) pályarendszer egyenlete, ahol x és y a test koordinátái.
és
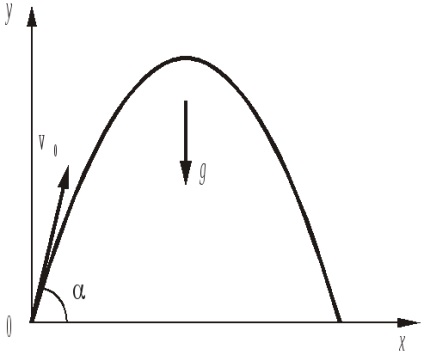
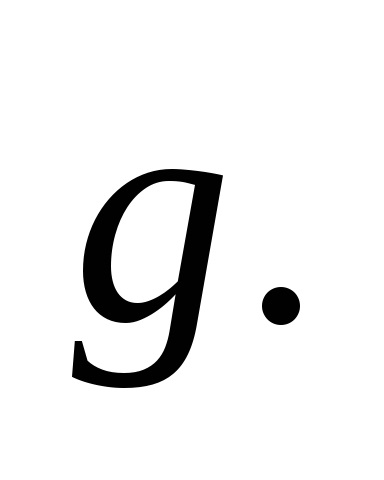
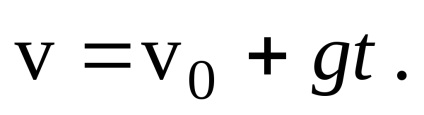
Megtaláljuk a sebességvektor vetületét a koordinátatengelyeken, miután ezt az egyenletet az x és y tengelyekre terveztük:
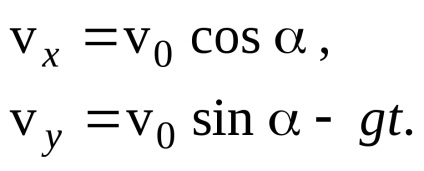
A vektor modulusának és a Descartes-tengelyekre mutató projekciói közötti kapcsolatból a következőket kapjuk:
b) Ha a sebességvektor és a vízszintes tengely közötti szög egy bizonyos időpontban t1. akkor:
c) A test mozgás törvényét vektoros formában jegyezzük meg, figyelembe véve, hogy a kezdeti időpontban a test a koordináták eredőjeként jött létre.
itt
Ezt az egyenletet az y-tengelyre tervezzük:
Megtaláljuk a test T repülési idejét azzal a feltétellel, hogy ebben az időpontban az y = 0 koordinátája:
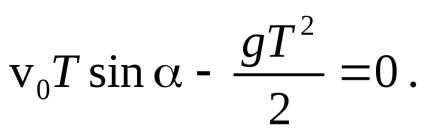
A kapott T1 = 0 egyenlet egyik gyökere megegyezik a test kezdeti pozíciójával, a másik gyökér adja a test repülési idejét:
d) Az (1) egyenletet vetjük az x tengelyre:
Találjuk meg a L testület repülési tartományát az L = x (T) állapotból:
Annak érdekében, hogy meg lehessen határozni a H. maximális emelési magasságot, a test repülési idejét a pálya legmagasabb pontjára találjuk azzal a feltétellel, hogy ebben az időben a sebességvektor

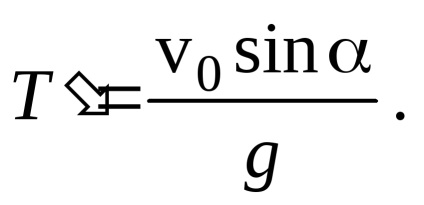
Ne feledje, hogy a Talla felemelkedési idő megegyezik a repülési idő felével. Következésképpen az emelkedési idő megegyezik a süllyedés idejével.
e) A (2) és (3) kapcsolatok által meghatározott koordinátaformában a mozgás törvény lényegében meghatározza a trajektória egyenletét a t paraméteren keresztül. E paraméter kizárásával a pálya egyenletét explicit formában kapjuk meg:
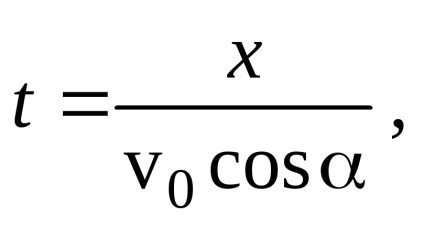
A (4) bekezdésből következik, hogy a horizonton szöget bezáró test pályája egy parabola, amelynek ágai lefelé irányulnak (x 2 koefficiens negatív). A parabola áthalad a származáson (az y (x) = 0 egyenlet egyik gyökere nulla).
2. A repülőgép h = 500 m magasságban repül vízszintes egyenes vonal mentén, v0 = 100 m / s sebességgel. A pilótának le kell dobnia a bombát a célba, ami a repülőgép előtt áll. Mekkora szögben a függőleges, ha látja a célpontot a pillanat alatt a bombát?
P
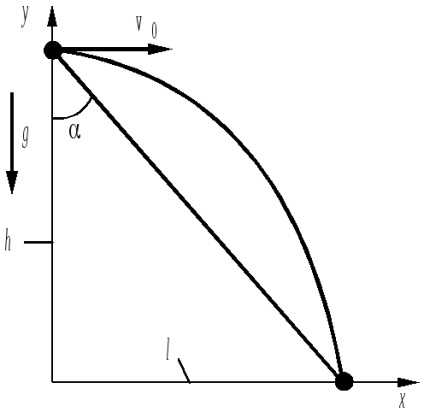
A keresett szöget a nyilvánvaló összefüggés határozza meg:
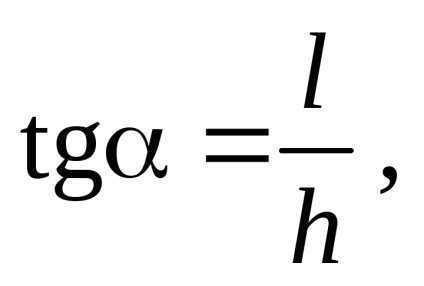
ahol l a vízszintes tartomány. Ez az érték megegyezik a t = v0t értékkel. ahol t a bomba repülési ideje állapota állapota
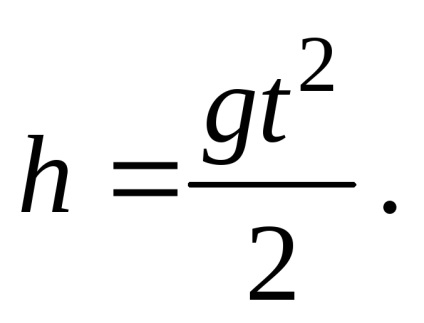
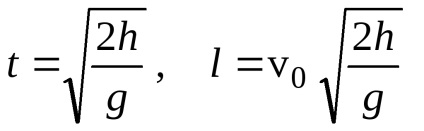
;
3. Milyen szögben kell a kőzetet olyan sebességgel dobni, amely v0 = 20 m / s, mely horizonton vízszintesen kell repülnie, mielőtt a talajba esne
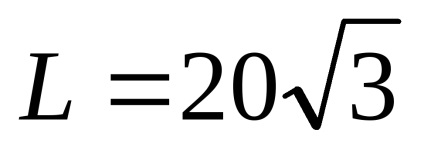
A megoldás. Írd meg a kapcsolatot a repülési tartomány között. a kezdeti sebesség v0. a gravitáció g szöge és gyorsulása (lásd e szakasz 1. feladatának 3. pontját):
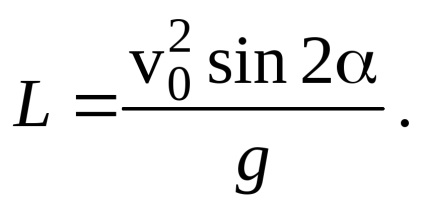
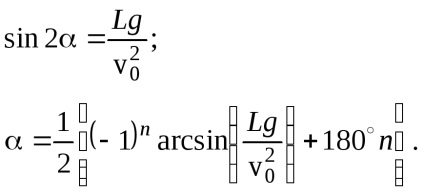
Itt n olyan egész számok, amelyek értékei a nyilvánvaló állapotból származnak:
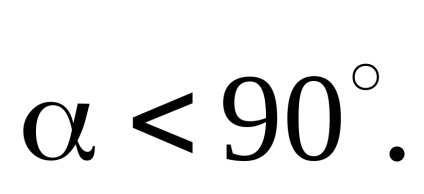
Legyen n = 0. Akkor
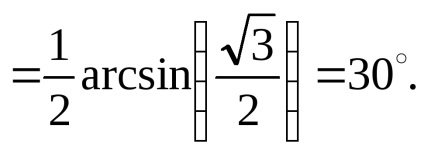
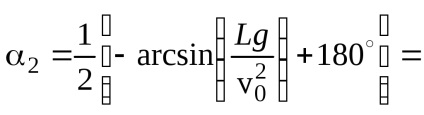
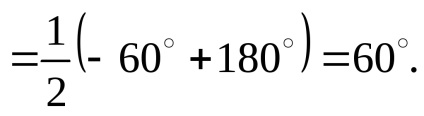
Más n érték esetén a szög> 90 °. Tehát a szükséges szögek:
4. A kőt vízszintesen dobták nagy magasságból egy sebességgel
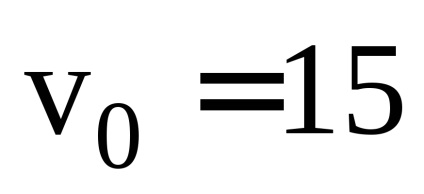
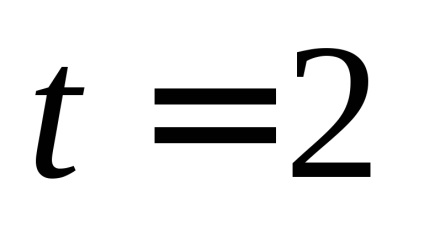
a) sebesség


b) a kő elmozdulási vektorának modulusát.
A megoldás. a) A (1.12) kifejezéssel összhangban a kő sebessége
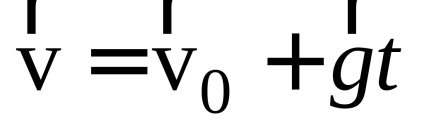
ahol
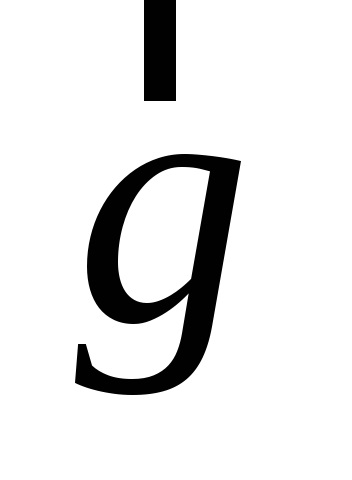
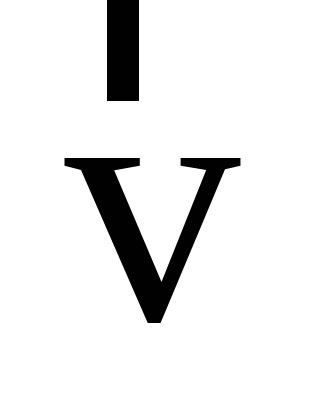
Definíció szerint és
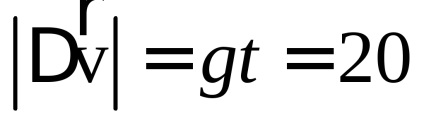
b) Az elmozdulási vektor
,
ahol