Homogén lineáris egyenlet megoldása állandó koefficiensekkel, matematikai problémák megoldásával
Homogén lineáris egyenlet megoldása állandó koefficiensekkel.
Előző Tartalom Következő
A forma egyenlete
egy homogén lineáris egyenlet, állandó koefficiensekkel. A megoldás a jellemző egyenlet gyökerei alapján készült.
Ez a homogén egyenlet megfelel a jellemző egyenletnek:
.
és legyen gyökere. akkor:
1) Ha az 1 sokszorosulás valódi gyökere, akkor a forma általános megoldásának ideje
2) Ha a k multiplicitás igazi gyökere, akkor megfelel a forma általános megoldásának kifejezésnek, ahol az 1-es fokozat polinomiája (az indefinite koefficiensekkel) kisebb, mint a gyökér sokasága; például ha a gyökér. az
3) Ha van egy pár konjugált komplex gyökér, akkor
4) Ha - a k multiplicitású komplex konjugált gyökerei, akkor a koszinusz és a szinusz előtt nem csak állandók, hanem k-1 fokú polinomok íródnak.
példák:
1. példa.
Oldja meg az egyenletet:
Megfogalmazzuk és megoldjuk a jellemző egyenletet
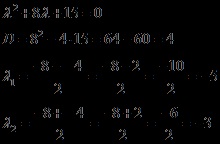
Az 1. többszörös tényleges gyökereket (azaz 1-et) kaptuk, akkor a homogén egyenlet általános megoldása a következőképpen alakul:
válaszolni:
2. példa.
Oldja meg az egyenletet:
Megfogalmazzuk és megoldjuk a jellemző egyenletet
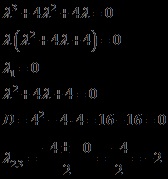
Három valós gyökeret szereztünk.
(multiplicity - 1) és (mivel 2 darabuk ugyanaz, a sokaság 2). akkor a homogén egyenlet általános megoldása a következőképpen alakul:
Megjegyzés, mivel a root -2-nek sokasága 2, akkor a megfelelő összegző tényező nem egyszerűen C, hanem az első fok polinomának általános alakja, fokban, a gyökér 1 kisebb sokaságában.
válaszolni:
3. példa.
Oldja meg az egyenletet:
Megfogalmazzuk és megoldjuk a jellemző egyenletet
Készítettünk egy pár komplex konjugált gyökeret az 1. sokaságból
. akkor a homogén egyenlet általános megoldása a következőképpen alakul:
válaszolni:
4. példa.
Oldja meg az egyenletet:
Megfogalmazzuk és megoldjuk a jellemző egyenletet
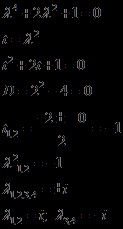
Két azonos páros komplex konjugált gyökeret kaptunk; sokoldalúság 2
. akkor a homogén egyenlet általános megoldása a következőképpen alakul:
válaszolni: