A grafikonokkal kapcsolatos problémák megoldása - matematika, leckék

Lecke kíséretében bemutatása, amely a különböző típusú problémák a használata grafikonok: a probléma megoldódott a végfelhasználás aritmetikai maradékainak problémát érdeke a probléma, amelyen meghatározott sík gráf szükséges ábrázolni felemelése nélkül ceruzát a papír és nem körülveszi kétszer ugyanazon a grafikonon plot . Elméletileg az anyagot a lecke tartalmaz a koncepció a gróf, egy él, páros, páratlan grafikon lecke a következő lépéseket tartalmazza: a szóbeli beszámolót, ellenőrizze otthoni használatra munka-counter játék, házi feladat, lecke összefoglalója. A bemutató történelmi anyagot tartalmaz Eulerről és szép kijelentésekről.
A problémákat az 5. fokozatú grafikonok segítségével oldja meg.
a grafikon fogalmának megszilárdítása és a grafikonok használatának készségeinek fejlesztése a problémák megoldása érdekében;
ellenőrizze a grafikon koncepciójának elsajátításának szintjét a rendelkezésre álló ismeretek új problémák megoldására való képességén keresztül.
a diákok logikus és kreatív gondolkodásának fejlesztése, leleményesség, megfigyelés, intuíció és megfelelőség az osztálytárs munkájának értékelésében;
aktív kognitív érdekeket képviselnek a témában.
A történelmi személyiségek tiszteletének oktatása, az irodalom iránti szeretet a kiválasztott feladatok szövegének példáján.
1. Szervezeti momentum
2. A házi feladat ellenőrzése
"Az élet két kérdéssel van díszítve: a matematika megszállása és tanítása" Poisson S.II.
A matematika tanulmányozása a problémák és a gyakorlatok megoldásának folyamatában történik.
Srácok, ma a leckében fogjuk megoldani a grafikonokkal kapcsolatos problémákat, megoldani a végén, a maradványok aritmetikáját, százalékos feladatokat felhasználva.
Kezdjük az otthoni feladattal érdeklődésre
5 · 0,35 = 1,75 liter zsír 5 liter tejszínben
4 · 0,20 = 0,8 liter zsír 4 literben
1,75 + 0,8 = 2,55 liter zsír a keverékben
5 + 4 + 1 = 10 literes keverék
5. 2.55: 10 = 0.255 liter = a keverék 25,5% zsírtartalma
Mi lesz a játék: "A legjobb számláló" (az értékeléshez).
Válasszon ki minden sorból 2 számlálót.
Pestalozzi azt is elmondta: "A számlák és a számítások a végrendelet alapját képezik"
Ismerjük meg, hogy melyik helyesen válaszoljon több kérdésre. Srácok, segíts - számold ki a gyerekek helyes válaszát.
1) Fizikus, fáradt, 22: 00-kor lefeküdt; elő-riasztás a következő nap 12 órájában. Hány órát aludt, mielőtt az ébresztőóra felébresztené? [2]
4) Mekkora marad a terméknek a 6-os elosztásával?
67 = 1 (Mod 6) (Ez a feladat a maradék aritmetikai feladatoknál)
5) Keresse meg a további részarányt 5 következő összeggel (7 + 56 + 558 + 5558) / 5
6) A yp - e megoldása: (((x + 2) / 4) -2) * 6 = 12 [14]
7) Keresse meg a számot, ha 3% -a 24 [800]
9) 3000% -a 50 [1500]
10) Keresse meg a 48 és 16 közötti számot [300%]
11) Számolja ki a 700 [0.7] érték 0,1%
Mindenki megnyerte, mert mindenki részt vett velük, és ellenőrizte a válaszok helyességét.
4) Kiváló női matematikus Kovalevskaya hangsúlyozta: "Matematikusok
van egy nyelv - ezek a képletek "
Problémák megoldódtak a végén
(Jelenet) "A paraszt és az ördög":
A paraszt megy és sír: "Ehma! Az életem keserű! Zaela-nak feltétlenül szüksége van! Itt a zsebében csak néhány filléres réz sodort, és most el kell adni őket. És hogyan történik másokkal, hogy pénzt kapnak az összes pénzért? Legalább valaki segítene nekem.
Csak ideje volt erre mondani, hogy nézzen, és előtte az ördög áll.
-Nos, - mondja - ha akarsz, segítek neked. És ez egyáltalán nem nehéz. Látod ezt a hidat a folyón?
-Látom! - mondja a paraszt, és ő maga megrémült.
-Nos, ezért érdemes, hogy csak átkeljen a hídon - kétszer annyi pénzt kapsz, mint amilyen van. Visszatér, ismét kétszer annyi lesz, mint volt. És minden alkalommal, amikor áthalad a hídon, kétszer annyi pénzt kapsz, mint az átkelés előtt.
-Ó, ez? - mondja a paraszt.
-A helyes szó! - biztosítja az ördögöt. - Csak bátorság, meggyőzés! Az a tény, hogy kettős pénzem, minden alkalommal, amikor áthalad a hídon, adjon nekem 24 kopeckot. Egyébként nem értek egyet.
-Nos, nem számít! - mondja a paraszt. - Miután egyszer a pénz megduplázódott, akkor miért ne adjon 24 kopecket minden alkalommal? Nos, próbáljuk meg!
Egyszer átjutott a hídon, számolta a pénzt. Valójában kétszer akkora lett. Feladta 24 kopeckát az ördögnek, és átkelt a második alkalommal. Ismét kétszer annyi pénz volt, mint korábban. 24 copecket számolt, megadta a vonalat, és harmadik alkalommal áthaladt a hídon. A pénz ismét kétszer annyi. De csak kiderült, hogy mindössze 24 kopecks voltak, amelyek megállapodás alapján kötelesek voltak megadni a vonalat. Elengedte őket, és penny nélkül maradt.
Mennyibe került először a parasztnak a pénz?
1. ((x 2 - 24) 2 - 24) 2 - 24 = 0 x = 21
Ha az utolsó átmenetet a paraszti fordult 24, hogy mielőtt 12, csatlakozott hozzájuk 24 (adta) megkapjuk az eszközök 36 a második átmenet volt 38 kopecks. Hozzáadtak nekik 24, 42-et kapunk, vagyis 21 zsaruk van.
Elvesztette a parasztot. Látható, hogy valaki más tanácsait mindig saját magának kell meghoznia.
5. Grafikus feladatok.
A grafikonok elmélete nemcsak a matematikában, hanem a geoinformációs rendszerekben (GIS) is megtalálható. .. A meglévő vagy újonnan kialakított lakások, épületek, városrészek, stb minősülnek a tetején, és bekötő utak, közüzemi hálózatok, elektromos vezetékek, stb - .. Mivel a bordák. Alkalmazása különböző számításokat végezni, mint egy grafikon, amely lehetővé teszi például, hogy megtalálják a legrövidebb kitérő vagy a legközelebbi élelmiszerbolt, terv a legjobb útvonalat.
Az első feladattípus
- Ki játszik Lyapkin-Tyapkinnak?
Az iskolai dráma körében úgy döntött, hogy felállítja Gogol "felügyelőjét". Aztán kitört egy fűtött érv. Mindez Lyapkin-Tyapkinnel kezdődött. - Lyapkin-Tyapkin lesz velem! mondta Gene határozottan.
- Nem, én leszek Lyapkin-Tyapkin - tiltakozott Dima.
- Gyermekkorom óta álmodtam, hogy megtestesítsem ezt a képet a színpadon.
- Nos, igen, egyetértek azzal, hogy feladom a szerepet, ha megengedik, hogy Khlestakovot játszhassam - mutatta Gen generálódását.
-. És én - Osip -, nem adtam hozzá Dima nagylelkűségében. - Én vagy Eper vagy kormányzó akarok lenni - mondta Vova.
- Nem, én vagyok a kormányzó - kiáltotta Alik és Bory. "Vagy Khlestakov" - tette hozzá egyszerre.
A szerepeket elosztják, hogy az előadók boldogok legyenek? (Nem kérdezzük meg, hogy elégedett lesz-e a közönség.)
Minden egyes résztvevő közül a szegmenseket húzzuk, azaz A szélei azoknak a szerepeknek, amelyeket ő szeretne játszani. Van egy tíz csúcsa és tíz széle. Tízből kell választani az öt széleket, amelyeknek nincs közös csúcsa.
Gina Dima Vova Boria Alik
Lyachpin-Khlestakov Osip Eper
Könnyűvé tenni. Érdemes megjegyezni, hogy egy csúcs a 3. és 4. csúcshoz vezet, a DiB csúcstól. Ez azt jelenti, hogy az Osip (top 3) Dima-nak (aki másnak) és Strawberry Vova-nak kell játszania. Vertex 1 Lyapkin- Tyapkin-élek kötik össze, hogy a D és E. Rib 1- D szükségtelen, mert Dima már foglalt, a FIN 1 G, Lyapkina- Tyapkina játszani Gene. Továbbra is az A és a B csúcsokat kell összekötni a 2. és 5. csúcsokkal, amelyek megfelelnek Khlestakov és Gorodnichy szerepének. Ezt kétféleképpen lehet elvégezni: válaszd az A-5 és a B-2 széleket, vagy az A-2 és a B-5 éleket. Az első esetben Alik fog játszani a kormányzó, és Boria-Khlestakov, a második esetben, éppen ellenkezőleg. A grafikonunk szerint nincs más megoldás a problémára.
A második típusú feladatok. amelyben egy adott sík gráfot kell húzni, anélkül, hogy a ceruzát a papírból vették volna, és nem görbölte volna kétszer a grafikon két szakaszát. Ha ebben az esetben egy zárt vonal ugyanazon a csúcson kezdődik és végződik, akkor egy ilyen gráfot Euler's neveznek
Ha a gráf összes csúcsa egyenletes, akkor a grafikon egy ciklusban megkerülhető anélkül, hogy egyetlen él kétszer anélkül.
Ha 2 csúcsait páratlan, a zárt nem létezik, de lehet jön egy furcsa csúcsok körül az egész grafikonon, és vissza az első, a második páratlan.
1. Az anekdota jól ismert: Valaki 1000000 rubelt adott mindenkinek, aki felhívja a következő számot.
Követelmény: egy folyamatos löketnél, azaz anélkül, hogy levenné a tollat vagy a ceruzát a papírról, és nem vonná össze a sorokat.
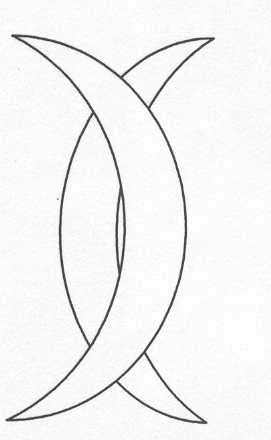
2
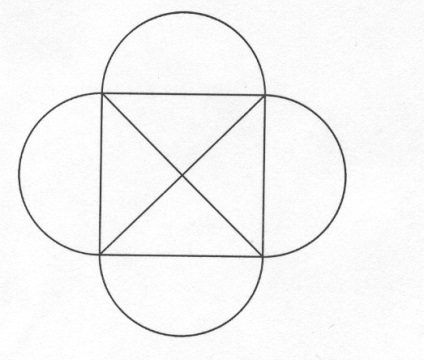
. Mohammed, az aláírás helyett (írástudatlan volt), egy lökettel írva, amely a következőkből áll:
3
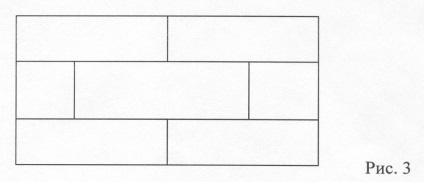
. A 3. ábrán látható ábra egyetlen ütemben nem húzható le. Mutassa be, miért
4. A légy a cukor alá jött a palackba. A bank kocka alakú. Hogy a légy folyamatosan megkerülje a kocka mind a 12 élét, anélkül, hogy kétszer megy az egyik szélén, nem szabad ugrálni és repülni egy helyről a másikra a helyén.
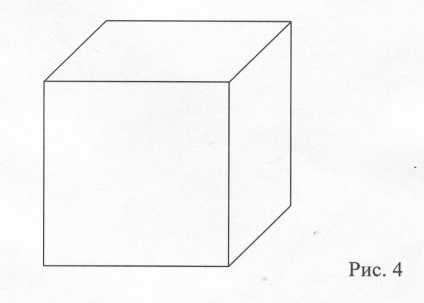
Niven megjegyezte: "A matematikát nem lehet tanulmányozni, ha megfigyeljük, hogyan végzi a szomszéd"
6. Házi feladat: Lehet-e a rajzokon ábrázolt ábrákat egy lökettel festeni? (megoldva a grafikon segítségével)
Ma már találkoztunk egy másik módszerrel a problémák megoldására grafikonok segítségével.
Ezeknek a feladatoknak a tanulságos oldala annak vizsgálata, hogy lehetséges-e megoldani ezt a problémát, mielőtt a megoldásról döntene.
Ismét azt láttuk, hogy a gráfelmélet lehet oldani gyorsan és elegánsan feladatokat, amelyeket nagyon nehéz megoldani más módszereket és lehetővé teszi, hogy ne csak megoldani az egyik probléma külön-külön, hanem meg kell találnia megoldási módjait, egy osztály a problémák.
Végezetül azt szeretném mondani a következő szavakat: "Azoknál a feladatoknál, amelyeket az élet elé állít, az elbíráló maga a természet.