A determinánsok bizonyos tulajdonságai

előző ◈ a következő

Itt leírjuk azokat a tulajdonságokat, amelyeket általában a magasabb matematika standard tanfolyamában meghatározó determinánsok kiszámítására használnak. Ez egy kiegészítő téma, amelyet a fennmaradó részekről szükség szerint hivatkozni fogunk.

Tehát hagyjunk egy négyzetmátrixot $ A _ = \ left (\ begin a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ ldots \\ a_ a_ \ ldots a_ \\ \ end \ right) $. Minden négyzetes mátrixnak van egy meghatározója (vagy meghatározója). Nem fogok belemenni a koncepció lényegébe. Ha magyarázat szükséges, kérjük, iratkozzon le a fórumra. és részletesebben foglalkozom ezzel a kérdéssel.

A $ A $ mátrix meghatározóját $ \ Delta A $, $ | A | $ vagy $ \ det A $ jelöli. A meghatározó sorrendje megegyezik a sorok (oszlopok) számával.

A meghatározó értéke nem változik, ha annak sorai helyébe a megfelelő oszlopok lépnek; $ \ Delta A = \ Delta A ^ T $.

Példa erre a tulajdonságra: mutasd / elrejt

Tekintsük a $ \ left | meghatározót \ begin 2 5 \\ 9 4 \ end \ right | $. Találjuk meg az értékét az 1. képlet segítségével, a második és a harmadik megbízás meghatározóinak számításakor.

$$ \ left | \ begin 2 5 \\ 9 4 \ end \ right | = 2 \ cdot 4-5 \ cdot 9 = -37. $$

A sorokat oszlopokkal helyettesítjük az elvvel: "az első sor az első oszlop volt", "a második sor a második oszlop volt":

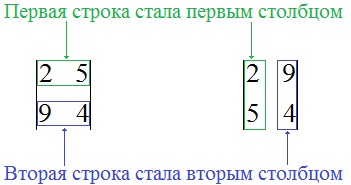
Az eredményül kapott determinantot kiszámítjuk: $ \ left | \ begin 2 9 \\ 5 4 \ end \ right | = 2 \ cdot 4-9 \ cdot 5 = -37 $. Amint láthatja, a meghatározónak a csere helyére vonatkozó értéke nem változott.

Ha a meghatározó két sorát (oszlopokat) váltja fel, akkor a determináns jele az ellenkezőjére változik.

Példa erre a tulajdonságra: mutasd / elrejt

$$ \ left | \ begin 2 5 \\ 9 4 \ end \ right | = 2 \ cdot 4-5 \ cdot 9 = -37. $$

Most kicseréljük az első és a második sorokat. Megkapjuk a $ \ left | meghatározót \ begin 9 4 \\ 2 5 \ end \ right | $. Az eredményül kapott determinantot kiszámítjuk: $ \ left | \ begin 9 4 \\ 2 5 \ end \ right | = 9 \ cdot 5-4 \ cdot 2 = 37 $. Tehát a kezdeti determináns értéke (-37) volt, és a sorrend változó sorrendjével a meghatározó értéke $ - (-37) = 37 $. A determináns jele ellentétes irányban változott.

A meghatározó, amelyre a sor (oszlop) összes eleme nulla, nulla.

Példa erre a tulajdonságra: mutasd / elrejt

Mivel a meghatározó $ \ left | \ begin -7 10 0 \\ -9 21 0 \\ 2 -3 0 \ end \ right | $ a harmadik oszlop összes eleme nulla, akkor a determináns nulla, azaz. $ \ left | \ begin -7 10 0 \\ -9 21 0 \\ 2 -3 0 \ end \ right | = 0 $.

Olyan meghatározó, amelynek egy sor (oszlop) összes eleme egyenlő egy másik sor (oszlop) megfelelő elemével, nulla.

Példa erre a tulajdonságra: mutasd / elrejt

Mivel a determinisztikus $ \ left | \ begin -7 10 0 \\ -7 10 0 \\ 2 -3 18 \ end \ right | $ Az első sor összes eleme megegyezik a második sor megfelelő elemeivel, akkor a determináns nulla, azaz. $ \ left | \ begin -7 10 0 \\ -7 10 0 \\ 2 -3 18 \ end \ right | = 0 $.

Ha a determinánsban egy sor (oszlop) összes eleme arányos egy másik sor (oszlop) megfelelő elemeivel, akkor az ilyen determináns nulla.

Példa erre a tulajdonságra: mutasd / elrejt

Mivel a meghatározó $ \ left | \ begin -7 10 28 \\ 5 -3 0 \\ -15 9 0 \ end \ right | $ a második és a harmadik vonal arányos, azaz. $ III = -3 \ cdot II $, akkor a determináns nulla, azaz. $ \ left | \ begin -7 10 28 \\ 5 -3 0 \\ -15 9 0 \ end \ right | = 0 $.

Ha egy sor (oszlop) minden elemének közös tényezője van, akkor ez a tényező a determináns jelein kívül vehető el.

Példa erre a tulajdonságra: mutasd / elrejt

Tekintsük a $ \ left | meghatározót \ begin -7 10 \\ -9 21 \ end \ right | $. Ne feledje, hogy a második sor összes elemét 3:

$$ \ left | \ begin -7 10 \\ -9 21 \ end \ right | = \ balra \ begin -7 10 \\ 3 \ cdot (-3) 3 \ cdot 7 \ end \ right | $$

A 3. szám a második sor összes elemének közös tényezője. A meghatározó tényező jeleit a következőképpen vesszük:

$$ \ left | \ begin -7 10 \\ -9 21 \ end \ right | = \ balra \ begin -7 10 \\ 3 \ cdot (-3) 3 \ cdot 7 \ end \ right | = 3 \ cdot \ balra \ begin -7 10 \ -3 7 \ end \ right | $$

A meghatározó nem változik, ha a sor minden eleméhez (oszlop) egy másik sor (oszlop) megfelelő elemeit hozzáadja tetszőleges számhoz.

Példa erre a tulajdonságra: mutasd / elrejt

Tekintsük a $ \ left | meghatározót \ begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | $. Adja hozzá a második sor elemeit a harmadik sor megfelelő elemeihez, ezt 5-tel megszorozza. Írja be ezt a következőképpen:

$$ \ left | \ begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | \ begin \ phantom \\ II + 5 \ cdot III \\ \ phantom \ end $$

A második sort megváltoztatják, a többi sor változatlan marad.

$$ \ left | \ begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | \ begin \ phantom \\ II + 5 \ cdot III \\ \ fantom \ end = \ balra \ begin -7 10 0 \\ -9 + 5 \ cdot 2 21 + 5 \ cdot (-3) 4 + 5 \ cdot 1 \\ 2 -3 1 \ end \ right | = \ balra \ begin -7 10 0 \\ 1 6 9 \\ 2 -3 1 \ end \ right |. $$

Ha a determinánsban egy bizonyos sor (oszlop) más sorok (oszlopok) lineáris kombinációja, akkor a determináns nulla.

Példa erre a tulajdonságra: mutasd / elrejt

Azonnal megmagyarázom, hogy mi a "lineáris kombináció" kifejezés. Tegyük fel, hogy vannak sorok (vagy oszlopok): $ A_1 $, $ A_2 $. $ A_s $. kifejezés

$$ k_1 \ cdot A_1 + k_2 \ cdot A_2 + \ ldots + k_s \ cdot A_s, $$

ahol $ k_i \ in R $ a lineáris (lineáris) kombinációnak nevezik $ A_1 $, $ A_2 $ sorokat. $ A_s $.

Például, fontolja meg egy ilyen meghatározó tényezőt:

$$ \ left | \ begin -1 2 3 0 \ -2 -4 -5 1 \ 5 0 7 10 \ -13 -8 -16 -7 \ end \ right | $$

Ebben a meghatározóban a negyedik vonal az első három sor lineáris kombinációjával fejezhető ki:

$$ IV = 2 \ cdot I + 3 \ cdot II-III $$

Következésképpen a vizsgált determináns nullával egyenlő.

Ha minden egyes eleme valamely k-dik sora (k-edik oszlopa) a determinánst összegével egyenlő a két kifejezést, mint determináns megegyezik az összeg a determinánsok az első, amely a k-adik sor (K-edik oszlop) először kifejezések, és a második meghatározó a k-es sorban (k-es oszlop) a második összeg. Ezen determinánsok egyéb elemei ugyanazok.

Példa erre a tulajdonságra: mutasd / elrejt

Tekintsük a $ \ left | meghatározót \ begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | $. A második oszlop elemeit az alábbiak szerint írjuk: $ \ left | \ begin -7 3 + 7 0 \\ -9 21 + 0 4 \\ 2 5 + (-8) 1 \ end \ right | $. Ezután az ilyen determináns megegyezik a két determináns összegével:

$$ \ left | \ begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | = \ balra \ begin -7 3 + 7 0 \\ -9 21 + 0 4 \\ 2 5 + (-8) 1 \ end \ right | = \ balra \ begin -7 3 0 \\ -9 21 4 \\ 2 5 1 \ vég \ jobbra + \ balra \ begin -7 7 0 \\ -9 0 4 \\ 2 -8 1 \ end \ right | $$

Az azonos rendű két négyzetes mátrix termékének meghatározója megegyezik e mátrixok determinánsainak termékeivel, azaz $ \ det (A \ cdot B) = \ det A \ cdot \ det B $. A szabály általánossága: $ \ det \ bal (A ^ n \ jobb) = \ bal (\ det A \ jobb) ^ n $.

Ha a $ A $ mátrix nem degenerált (vagyis annak meghatározója nem egyenlő nulla), akkor $ \ det \ left (A ^ \ right) = \ frac $.

A meghatározó tényezők kiszámítására szolgáló képletek

A második és a harmadik megbízás meghatározó tényezői a következő képleteket igazolják:

A $ A_ $ mátrix meghatározója kibővíthető az i-edik sorban az alábbi képlet segítségével:

Ennek a képletnek analógja létezik az oszlopokra. A meghatározónak a j oszlop feletti kiterjesztésére szolgáló képlet a következő:

Jelöljünk még egy képletet a felső háromszög és alsó háromszög mátrixok determinánsainak kiszámítására (e kifejezések magyarázatát lásd a "Mátrixok: Mátrixfajták: Alapfogalmak" című témakörben). Az ilyen mátrix meghatározója megegyezik a fő átlós elemek termékével. példák:

\ begin \ left | \ begin 2 -2 9 1 \\ 0 9 8 0 \\ 0 0 4 -7 \\ 0 0 0 -6 \ end \ right | = 2 \ cdot 9 \ cdot 4 \ cdot (-6) = - 432. \\ \ left | \ begin -3 0 0 0 \\ -5 0 0 0 \\ 8 2 1 0 \\ 5 4 0 10 \ end \ right | = -3 \ cdot 0 \ cdot 1 \ cdot 10 = 0. \ end

Kapcsolódó cikkek

előző ◈ a következő