Trigonometrikus egyenlőtlenségek tangens, matematika-ismétléssel
A korábbi vizsgálatokban a következő típusú trigonometriai egyenlőtlenségeket oldottuk meg:
Ebben a leckében megoldjuk az egyenlőtlenségeket a tan tan> a.
A következő döntési algoritmust használjuk (mint az előző leckében):
1. Ha az argumentum összetett (különbözik az x-től), akkor cserélje ki t-rel.
3. Keresse meg a t értékének intervallumát. ahol a tangentum az y = a egyenes felett helyezkedik el. Ennek az intervallumnak a bal oldali határa arctg a. és a megfelelő mindig (π / 2)
4. Írja le a kettős egyenlőtlenséget a t argumentumra. figyelembe véve a legrövidebb tangens periódust T = π (t az arctg a és (π / 2) abszcisszák között).
5. Fordított helyettesítést (visszatérünk az eredeti argumentumhoz), és kifejezzük x értékét a kettős egyenlőtlenségből, írjuk a választ numerikus intervallum formájában.
Az egyenlőtlenség mindkét oldalát 3-mal osztjuk meg. Módosítsuk a változót t-re. Ezután egyszerűbb egyenlőtlenséget kapunk.
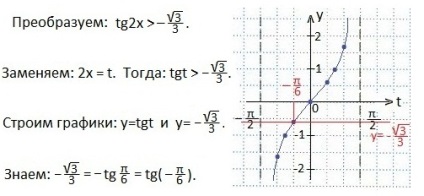
Határozza meg a t változó értéktartományát. amely szerint az egyenlőtlenség igaz. Ezek az y = tan t függvény grafikonjainak abszcisszái. amelyek az egyenes vonal felett helyezkednek el. Ezeket az értékeket keltetéssel ábrázoljuk. A t argumentum értékeit kettős egyenlőtlenségként írjuk le.
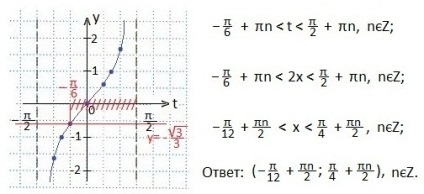
Az egyenlőtlenség bal oldalát a tg (α + β) képlet segítségével transzformáljuk, és egyszerűbb egyenlőtlenséget kapunk. Változást váltunk.

Határozza meg a t változó értékének kívánt tartományát. Ezután írja x-et, és írja meg a választ egy rés formájában. Figyelembe vesszük, hogy az egyenlőtlenség nem szigorú, de nincs tangens (π / 2).

A csökkentési képletekre vonatkozó szabályt alkalmazzuk:
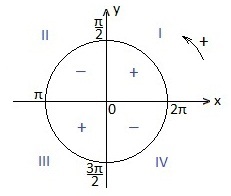
Érvelésünk a harmadik negyedévben van, a cotangent pedig a 3. negyedévben plusz jelzéssel rendelkezik. ezért a csökkentett funkció jele nem változik. Ennek az argumentumnak (π / 2) a rekordját háromszor (páratlan szám) vesszük, tehát a cotangent függvény az együttműködési tangensre változik.
Most az adott egyenlőtlenség a következőképpen alakult: tgt≥1. Az y = tgt és y = 1 függvények grafikonjait hozzuk létre. Határozza meg a t argumentum értékének intervallumát. amely szerint a tgt≥1 egyenlőtlenség igaz. A választ rés formájában írják le. Az egyenlőtlenség nem szigorú, de az intervallum jobb vége nem lép be az egyenlőtlenség megoldásába, mivel nincs tangens (π / 2).
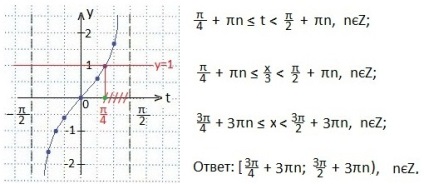
Kedves barátaim! Az egyenlőtlenségeket grafikus módon érintjük érintéssel, de természetesen van egy rövidebb megoldás - képletenként.
Ha tgt
Ha tan> a. akkor arctg a + πn
Ismerje meg ezeket a képleteket, és a trigonometrikus egyenlőtlenségeket a gyorsabb érintővel fogja megoldani!
Oldal 1/1 1