Hatékony határvonal és hatékony portfolió kiválasztása
Ha vesszük az összes eszközök, amelyek jelen vannak a piacon, és az összes lehetséges kombinációt (mappákat), a gépen „nyereségesség - kockázat” kap egy sor, hasonlóan ábrán látható. 7.6. A görbe borítékát hatékony határnak nevezik. Mivel a pozitív hatásai diverzifikáció nem teljesen korrelált eszközök, a lényeg a hatékony felderítő felel nem egyedi eszközök és portfóliók (az esetleges kivételeket - az eszköz maximális várható hozam és az eszköz minimális kockázat). Sőt, ha kombináljuk a portfolió mindegyik pár eszközök Line Plane „nyereségesség - kockázat”, amely megfelel a különböző arányú súlyok lesz a bal és a vonal fölé összekötő megfelelő pontokat kombinálásával pár portfóliók az új portfolió - tovább balra és fent és így tovább. és az effektív határ az összes ilyen vonal halmazának borítéka lesz.
Ábra. 7.6. Hatékony határok, mint kockázatos portfóliók bura
A jövedelmezőség növelése a kockázat növekedését jelenti, de csak akkor, ha hatékony határokon halad. Ha a portfólió a tényleges árrés alatt van, akkor további diverzifikációval növelheti jövedelmezőségét a kockázat növelése nélkül. Az ellentétes kijelentés a "kockázati növekedés a nyereségesség növekedését jelenti" hibás - a piac semmiféle kockázatot nem nyer, és mindig lehetséges egy magas kockázatú és alacsony (vagy akár negatív) hozamú eszköz megtalálása.
A tényleges határ mindegyik pontja egy hatékony portfóliónak felel meg. A portfólió akkor érvényes, ha más portfólió nem nyújt magasabb várt hozamot ugyanolyan szintű várt kockázattal, vagy alacsonyabb kockázattal rendelkezik, ugyanolyan megtérülési rátával.
A hatékony portfolió kiválasztása a befektető kockázati hajlandóságától függ. A kockázati hajlandóságot általában az úgynevezett hasznossági funkció jellemzi. Ez a függvény azon a feltevésen alapul, hogy a kockázat növekedésével a befektető növekvő hozamot igényel (a befektetők magatartását empirikus megfigyelések igazolják). A "hozamkockázat" síkon az egyes befektetők hasznossági funkcióját egy második rendű görbék családja látja el, amelyek mindegyike pontból áll, "hasznos", és a "segédprogram" akkor növekszik, amikor a görbék balról felfelé mozdulnak.
Ábra. 7.7. Az optimális portfolió kiválasztása a hatékony határokon a befektető hasznossági funkciójának felhasználásával.
Hatékony határnál, ahogy a kockázat nő, a lejtő csökken - telítettség következik be. Valójában egy eszköz kockázatossága legalább a végtelenségig nőhet - mivel a befektetők elkerülik a kockázatot, az ilyen eszközöket mindig megtalálják. De a magas nyereségesség érdekében a befektetőket vadászik, és az abszolút magas terméshozamú eszközök a piacon egyszerűen nem érhetők el. Így az 1. ábrán látható helyzet. 7,7, amely bemutatja a hatékony határt és családok hasznossági funkciók két befektető. Az U-görbék személyesítik a befektető preferenciáit, szemben a kockázattal, meredeken emelkednek (a kockázat növekedése miatt a befektető sokkal magasabb hozamot igényel). Az V. görbék egy olyan befektetőre utalnak, amely jobban tolerálja a kockázatot.
Curves index 1 átnyúló hatékony a két pontot, így minden befektető alkothatnak két mappákat, szubjektíve egyenértékű - nagyobb kockázatot jelentenek a második portfolió teljes mértékben kompenzálja a magasabb hozamot. Azonban, a magasabb közüzemi (vagy elégedettség), minden beruházó végezhetjük egy bizonyos átlagos állománya, nevezetesen amikor a segédprogram funkciót érinti hatékony határ (görbék index: 2) - egy pont csak egy befektetőnként (azzal jellemezhetők, hogy közüzemi funkció). Még kielégítő befektetők úgy érzik, a görbék index 3, de sajnos - nem zavarja a hatékony felderítő és portfolió a „hasznosság” nem alkotnak. Következésképpen az optimális portfolió, amelyek esetében a hasznossági függvény a hatékony határ - ez mind a hatékony, és a legtöbb „hasznos” a befektető.
A rij korrelációs koefficiens a két véletlen változó lineáris függősége irányának és fokának statisztikai mérőszáma (-1-től +1-ig változik). A 2. ábrán látható korrelációs együttható különböző értékeire vonatkozóan. 7.8 a megfelelő szórásdiagramokat adjuk meg. Zéró korrelációval az X és Y változók semmilyen módon nem kapcsolódnak egymáshoz - az Y teljesen véletlenszerűen változik, függetlenül az X változásoktól.
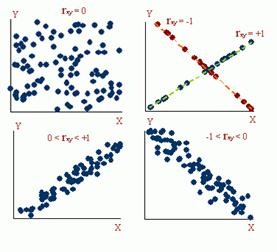
Ábra. 7.8. A korrelációs együttható különböző értékeire vonatkozó szóródási diagramok.
Amikor a korrelációs együttható abszolút értéke közeledik az egységhez, a változók közötti függőség egyre határozottabb lesz, amíg a véletlenszerűség teljesen megszűnik (a jobb felső sarokban lévő diagram). Az ábra a 3. ábra bal alsó sarkában található. 7.8 a korrelációs együttható abszolút értékben kissé nagyobb, mint a jobb alsó sarokban lévő diagram - a pontok a regressziós vonal közelebb vannak csoportosítva.
A korrelációs koefficiens négyzetét (mindig Rij 2-nek nevezzük) az elhatárolási együtthatónak nevezzük. Ez az együttható a regressziós vonalhoz tartozó adatok diszperziójának mértéke, és azt mutatja, hogy az Y függő változó változásának mekkora részét határozzuk meg (meghatározzuk) az X független változó megváltoztatásával.
Eszközértékelési elmélet (CAPM)
Az eszközértékelés elmélete (CAPM - Capital Asset Pricing Model) a hatékony portfolió elméletének folytatása. Pontosabban, ennek az elméletnek a terjedése a kockázatmentes eszköz hatékony portfóliójába való beépítéshez. Supplement kockázata eszközportfólió (az index A) riskless eszköz (index rf - kockázatmentes), amely, definíció szerint, a standard deviáció hozamok nulla (# 963; RF = 0). Nyilvánvaló, hogy a kockázatmentes eszköz bármelyik kockázatos eszközzel való kovarianziója nulla, mint a korrelációs együttható. majd
Így a kombinált portfolió mind a kockázata, mind a hozam lineárisan függ a kockázatos portfólió megfelelő értékétől. Ezért „hozam - kockázat” síkja az egyesített portfolió kockázata ellen függését néz ki, mint egy egyenes vonal a kockázatmentes eszköz bármely kockázatos portfóliók, hogy fekszenek a hatékony határon (lásd 7.9, közvetlen RRF A.). Annak érdekében, hogy növeljük a kitermelést (valamint a veszélye) együttes állománya, szükség van, hogy növelje a részesedése a kockázatos portfolió viszonyítva aránya kockázatmentes eszköz.
A portfólió hozamát meghatározó kifejezés újraírható
Világosan mutatja a portfolió jövedelmezőség és a hozam szórása közötti lineáris kapcsolatot. A vonal lejtése (RA - Rrf) / # 963; A az úgynevezett Sharpe arány.
Az A átváltási pont az effektív határ mentén és jobbra növeli a kombinált portfólió hatékonyságát (maximalizálja a Sharpe arányt) - ugyanazon kockázatok esetében a hozam egyre magasabb lesz. Mindennek azonban van egy határa - a maximális hatékonyság akkor érhető el, ha a kombinált portfóliónak megfelelő egyenes vonal hatékony határt ér el. Az érintkezési pontot általában M (piac) jelöli.
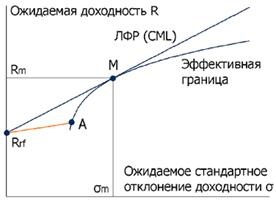
Ábra. 7.9 Tőkepiaci vonal (CML)
Természetesen, mivel a kockázatmentes eszköz az új, hatékony felderítő válik közvetlen RRF M (ábra 7.9.), Amely magasabb, mint a régi hatékony felderítő (portfoliók esetében kockázatos eszközök) kivételével mindenhol érintse a pontot M. Ezt a vonalat nevezzük tőkepiaci egyenes, rövidítve LRC (CML - tőkepiaci vonal). Minden befektetők választhatnak a portfolió a vonalon szerint az egyéni hasznosság függvény (a kapcsolattartási pont a hasznossági függvény és LRC). A különböző befektetőknek (különböző kockázatokkal rendelkező) portfóliói ugyanakkor csak a kockázatmentes eszköz arányában különböznek egymástól.
Így minden befektető ugyanazt a kockázatos portfóliót vásárolja (különböző részvényekbe), amelyek megfelelnek az M pontnak az effektív határon. Ezért az M portfóliónak tartalmaznia kell az összes kockázatos eszközt - mivel ha az eszköz nem szerepel az ilyen portfólióban, akkor azt jelenti, hogy nincs szükség rá, ezért az értéke nulla. Mivel feltételezzük, hogy a piac egyensúlyban van, szükség van arra, hogy az összes kockázatos eszközt az M portfóliójában piaci részesedésük arányában (részvények esetében - az állomány piaci árának terméke a forgalomban lévő részvények száma alapján) tartalmazza. Ha például az eszköz portfólión belüli részesedése magasabb, mint a tőkebefektetés aránya, az ilyen eszköz iránti túlzott kereslet növelni fogja az árát (és a kapitalizáció növekedését).
Az összes befektető számára kockázatos eszközök portfólióját piaci portfóliónak hívják. Mivel kivétel nélkül minden kockázati eszközt tartalmaz, teljesen diverzifikálódik - az eszközök összes egyedi kockázatát teljes mértékben kompenzálják. A piaci portfólióban csak szisztematikus kockázatot jelent, amelynek forrása a makrogazdasági instabilitás (ezért a befektetők ilyen nagy érdeklődést mutatnak a gazdaság állapotára vonatkozó adatok iránt). A legerősebb az ilyen mutatók, mint a GDP, az infláció, a kamatlábak, valamint a vállalati jövedelmezőség átlagos gazdasági szintjének szisztematikus változásának kockázata.
A portfólió diverzifikálásáról (a jellemzők közelítése a piaci portfólió jellemzőivel) az előző bekezdés tárgyalja. Itt megemlíthető, hogy a piaci portfolió rendszeres (nem változatos) kockázatát gyakran piaci kockázatnak nevezik. És a piaci portfóliónak a definícióból következő jó közelítése a tőzsdei súlyozású piaci index (nem töltöttünk annyi helyet az indexek leírásában). Az amerikai részvénypiacra a befektetők az SP 500 indexet célozzák meg, Oroszországot - az RTS indexet.
Ha egy befektető hajlandó a kockázat nagyobb, mint azt a ponton M (# 963; m), meg kell befektetni a kockázatos portfólió M több pénzt, mint ő, azaz a kölcsönt kössön a Rrf. Ebben az esetben a portfólió hozama és kockázata ugyanazokkal a képletekkel fejeződik ki, mint korábban, csak a Wrf negatívvá válik. És a nyereségesség és a szórás továbbra is lineáris függvények a megfelelő mennyiségeket a piaci portfolió, így a tőkepiaci egyenes csak továbbra is a jobb és felfelé. Figyelembe kölcsön megfelel az eltolás a sor a jogot M. Azonban bármilyen távolság nem lesz képes váltani - piaci szabályozók (SEC, az Egyesült Államok és az Orosz Szövetségi Értékpapír Bizottság) mennyiségének korlátozására kölcsön, amit megtehetsz a bróker biztonságára vonatkozó meglévő portfolió (letéti hitelek).
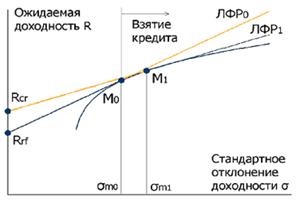
Ábra. 7.10 A tőkepiaci vonal a hitelkamatláb és a kockázatmentes tőke különbségével
A valóságban persze hitelkockázat-mentes arány magasabb (gyakran sokkal magasabb) és LRC válik szaggatott vonal (ábra 7.10.) - ez áll a szegmensek és LRK0 LRK1. LRK1 össze, kiindulva az a pont RCR (hitelezési ráta), és kapcsolódik a hatékony határ nem a „régi” pont M0. és jobbra és felette az M1 ponton. A lényeg M „hasít” - a befektetők számára a hitelek, a piaci portfolió kell egy kicsit kockázatos, de általában figyelmen kívül hagyják a különbségeket. Elhanyagolva a tény, hogy a pontok között az M0 és M1 portfolió kell kiválasztani a „régi” hatékony felderítő kockázatos eszközök, és érthető, hogy miért - érintőleges itt halad el a hatékony felderítő, és általában, ha kölcsön pénzt, sokat.