Simpson absztrakt módszere
1. Az integráció numerikus módszerei
2. A Simpson-képlet származtatása
4. Az integrációs lépés kiválasztása
1. Az integráció numerikus módszerei
A numerikus integráció problémája az integrál kiszámítása
az integrand értékek sorozatával.
A numerikus integráció problémáit olyan táblázatfunkció által meghatározott funkciókra kell megoldani, amelyek integráljait nem az elemi függvényekben, stb. Csak egy változó funkcióit tekintjük.
Az integrálandó funkció helyett integráljuk az interpolációs polinomiát. Alapuló módszerek cseréjét az integrandus polinom-interpoláció segítségével értékeli az eredmény pontossága, vagy egy adott pontossággal lehet választani ezeket a lehetőségeket a paramétereket a polinom.
Numerikus módszerek feltételesen csoportosíthatók az integrand approximációs módszerével.
A Newton-Cotes-módszerek egy függvény polinom általi közelítésén alapulnak. Ennek az osztálynak az algoritmusa csak a polinom mértékében különbözik. A közelítő polinom csomópontjai általában egyenlőtlenek.
A spline-integrációs módszerek a funkció függvényének egy spline-part polinom általi közelítésén alapulnak.
A módszerek a legmagasabb algebrai pontosság (Gauss-módszer) során speciálisan kiválasztott neravnootnosyaschie csomópontok, amelyek minimális hiba integrációt egy adott (kiválasztott) csomópontszám.
A Monte Carlo-módszereket leggyakrabban a több integrál kiszámítása során használják, a csomópontokat véletlenszerűen választják ki, a válasz valószínűségi jellegű.
A választott módszertől függetlenül, a numerikus integráció folyamatában ki kell számítani az integrál hozzávetőleges értékét, és becsülni kell a hibát. A hiba növekvő n-számmal csökken
egy szegmens partíciói. Ez azonban növeli a kerekítési hibát
összeadva a részleges intervallumokra számított integrál értékeket.
A csonkolási hiba az integrand tulajdonságaitól és a részszelet hosszúságától függ.
2. A Simpson képletének származtatása
Ha minden egyes szegmenspárhoz egy második fokú polinomot állítunk elő, majd integráljuk, és az integráns additivitási tulajdonságát használjuk, megkapjuk a Simpson-képletet.
Az integristát az intervallumra tekintjük. Ez az integrandot a második fokú Lagrange interpolációs polinommal helyettesítjük, amely a c pontokkal egyezik meg:
és a Simpson formula.
Az integrálra kapott érték egybeesik a tengely, a vonalak és a pontokon áthaladó parabola által határolt görbületes trapéz területével
Most becsüljük meg az integráció hibáját a Simpson-képlet segítségével. Feltételezzük, hogy y folyamatosan tartalmaz derivatívokat az intervallumon. Tegyük a különbséget
Mindegyik két integrál már lehet alkalmazni a középérték-tétel, mint a folyamatos és nem negatív függvény az első intervallum integráció nem pozitív, és a második (azaz nem változik jel minden egyes ilyen időközönként). ezért:
(az átlagérték tételt alkalmaztuk, mivel folyamatos függvény;).
A kétszeres differenciálást, majd az átlagos érték tételét alkalmazva egy másik kifejezésre jutunk:
Mindkét becslésből következik, hogy a Simpson-képlet pontosan a legfeljebb három fokú polinomokra jellemző. A Simpson-képletet például a következő formában írjuk:
Ha az integráció szegmense túl nagy, akkor egyenlő részekre (feltételezve), majd a szomszédos szegmensek mindegyik párjára oszlik. alkalmazza a Simpson formulát, nevezetesen:
A Simpson-képletet általános formában írjuk:
A Simpson-képlet hibája - a negyedik sorrendű módszer:
Mivel a Simpson módszer lehetővé teszi nagy pontosság elérését, ha nem túl nagy. Ellenkező esetben a másodrendű módszer pontosabb lehet.
Például, egy függvény esetében a trapéz alakú forma megadja a pontos eredményt, míg a Simpson formula általunk kapott
3. Geometriai illusztráció
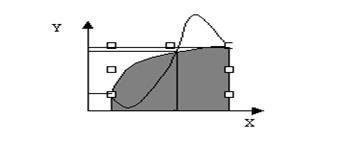
A 2h hosszúságú szegmensen egy parabola épül fel, amely három ponton halad át. Az OX tengely és az egyenes vonal közeiében elhelyezkedő parabola alatti területet az integrálnak kell tekinteni.
A Simpson-képlet alkalmazásának egyik sajátossága az, hogy az integrációs intervallum partícióinak száma egyenletes.
Ha a szegmensek száma a partíció - páratlan, akkor, az első három szegmens képletű kell alkalmazni, amely egy harmadik foka parabola, amely áthalad az első négy pont, hogy közelítse a integrandust.
Ez a Simpson "három-nyolcadik" formula.
Az integráció tetszőleges intervalluma esetén a (4) képlet kiterjeszthető; a részleges szegmensek száma három (többszörös) többszöröse lehet.
Meg lehet szerezni a magasabb rendű Newton-Cotes képleteket.
- a válaszfal szegmenseinek száma;
- az alkalmazott polinom foka;
- az első sorrendet a ponton;
Az 1. táblázat felsorolja az együtthatókat. Minden sor egy halmazcsoportnak felel meg a csomópontok számára a kt-teljesítmény polinom megalkotásához. Ha ezt a sémát több készletre szeretné használni (például k = 2 és n = 6), akkor "folytasd" az együtthatókat, majd hozzáadd őket.
A trapéz és a Simpson-képlet hibáinak becslésére szolgáló algoritmus a következő formában írható: (7),
ahol egy olyan együttható, amely az integráció módjától és az integrandum tulajdonságaitól függ;
h az integrációs lépés;
p a módszer sorrendje.
A Runge szabály a hiba kiszámítására szolgál az integrál kétszeres kiszámításával h és kh lépésekkel.
(8) utólagos becslés. Aztán I + = Ro (9), az integrál finomított értéke.
Ha a módszer sorrendje ismeretlen, akkor I-et kell számolni egy harmadik lépéssel egy lépéssel, azaz:
a három egyenlet rendszeréből:
ismeretlenekkel I, A és p kapunk:
A (10) bekezdésből következik, hogy (11)
Tehát az eljárás a kettős rendering, használt annyiszor, ahányszor szükséges, lehetővé teszi, hogy kiszámolja az integrál egy előre meghatározott pontossággal. A szükséges számú partíció kiválasztása automatikusan történik. A megfelelő integrációs módszerek szubrutinjaihoz többszörös hozzáférést is használhat, anélkül, hogy megváltoztatná ezeknek a módszereknek az algoritmusait. Azonban a módszerek alkalmazásával ravnootnosyaschie csomópontok, lehetséges, hogy módosítsa az algoritmusok és a felére csökkentik a számítások száma integrandus segítségével Riemann összegek felhalmozott az elmúlt integrációs intervallum több partíciót. Két közelítő értéke az integrálási és kiszámítása a trapéz módszerrel, és a lépések kapcsolódnak szerint:
Hasonlóképpen a képlet segítségével számított integrálok lépésekkel, és a következő kapcsolatok tartják:
4. Az integrációs lépés kiválasztása
Az integrációs lépés kiválasztásához használhatja a fennmaradó kifejezés kifejezését. Vegyük például a Simpson képlet hátralevő kifejezését:
Ha a ê ê , akkor ê ê .
Tekintettel az integrációs módszer pontosságára az utolsó egyenlőtlenségből, meghatározzuk a megfelelő lépést.
Ez a módszer azonban értékelést igényel (ami a gyakorlatban nem mindig lehetséges). Ezért a pontosság becslésének más módszereit használjuk, amelyek a számítások során lehetővé teszik a kívánt h lépés kiválasztását.
E módszerek egyikét elemezzük. enged
ahol a lépés lépcsőjének hozzávetőleges értéke. A lépést kétszer csökkentjük, a szegmenst két egyenlő részre osztjuk és ().
Tegyük fel, hogy nem túl gyorsan változik, tehát szinte állandó :. Aztán, és innen, ahonnan.
Ebből levonhatjuk a következő következtetést: ha tehát, ha ,, és a a szükséges pontosság, akkor a lépés alkalmas az integrál megfelelő pontosságú kiszámítására. Ha, akkor a számítás lépésekben, majd összehasonlításban történik, stb. Ezt a szabályt Runge-szabálynak nevezik.
Azonban az Runge politika alkalmazza hibaérték computing: csökkenő abszolút szerves számítási hiba növekszik (fordítottan arányos függőség), és elegendően kicsi nagyobb lehet, mint a hiba a módszer. Ha meghaladja ezt a lépést, a Runge szabály nem használható, és a kívánt pontosság nem érhető el. Ilyen esetekben meg kell növelni az értéket.
A Runge szabálya alapján lényegében azt a feltételezést alkalmazta, hogy. Ha csak egy táblázatot az értékek, akkor ellenőrizze „a állandóság” lehet tenni közvetlenül az asztalon további fejlesztése az algoritmus ugrás az alkalmazkodó algoritmus, amely szerint a választék a különböző integrációs lépést különböző részein a szegmens az integráció tulajdonságaitól függően csökkenti a számítások mennyiségét az integrandus.
Az integrált értékek finomításának másik rendszere az Einstein-folyamat. Az integrál lépésekkel számolható, és. Az értékek kiszámítása. Ezután (14).
A Simpson-módszer pontossága:
Példa 1. Számítsa ki az integráltat a Simpson képlet segítségével, ha egy táblázat adta meg. Becsülje meg a hibát.