A parabolák módszere (simpson módszer), az ingyenes kurzusdokumentumok, esszék és tézisek
A módszer lényege, hogy az integrát az [a, b] intervallumra a második fok interpolációs polinommal közelíti. vagyis egy függvény függvényének egy parabola parancsa.
A Simpson-formula (lásd az 1.5. Ábrát) a második fokú interpolációs polinóma integrálva van az [a, b] intervallumon:
hol. és - a funkció értékei a megfelelő pontokon (a szegmens végein és annak közepén).
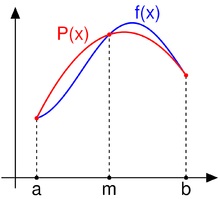
1.5. Ábra - Parabolikus módszer a ...
[a, b] partícionálás nélkül
Ellentétben módszerek téglalapok és trapézok ebben az esetben, az integrandus funkciót közelítjük a polinom másodfokú () nem az egyik, majd a két szomszédos lamella (lásd: Ábra 1.6). Ezért a szegmensek megosztásának szakaszszáma. egyenletesnek kell lennie.
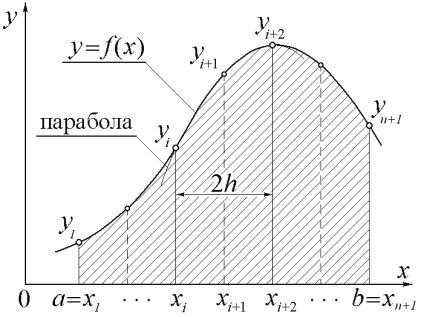
1.6. Ábra - Simpson módszere az integráció intervallumának megosztására egy egységes rács segítségével
A Simpson-módszerrel (a parabola-módszerrel) meghatározott definíciók kiszámításával kapcsolatos hiba a következő képlet alapján becsülhető meg:
hol van a negyedik származékos modul maximális értéke a telken. azaz A Simpson összetett formulája sokkal pontosabb, mint a négyszögek és a trapéz alakjai. Az [a, b] intervallum negyedik negyedpontja (Rn = 0 (h4)).
A hibás kifejezésekből látható, hogy a középső téglalapok és trapézok képletei pontosak az első fokú polinomok esetében, a lineáris függvények esetében, és a Simpson formula pontosan a polinomiákhoz a harmadik teljesítményig (számukra a hiba nulla).
A mérnöki gyakorlatban a hiba-becslési képletet nem használják, mert megköveteli a további probléma megoldását az integrandum magasabb származékainak megtalálásához. Egy kényelmesebb módszer a hiba becsléséhez egy meghatározott integrál kiszámításakor a Runge szabályon alapuló módszer (kettős számolási szabály). A végleges integrált értéket kétszer kell kiszámítani: egyszer egy integrációs lépéssel. és egy másik alkalommal kisebb integrációs lépéssel h2 = h1 / 2. A Runge-szabály relációja, amely az integrál approximált számításának minden módjára érvényes
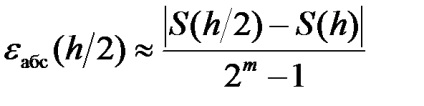
ahol S (h / 2) és S (h) az integrál hozzávetőleges értékei az [a. b], amelyek kétszer különböznek egymástól. A középső téglalapok és trapézek módszerei esetében az m = 2, a Simpson módszer m = 4. Ebből kiindulva, a kiválasztott lépéssel számított érték számításának becsléséhez meg kell ismételni a számításokat, meg kell duplázni a lépés méretét és a fenti összefüggést alkalmazni. Ha a probléma az eredménnyel kevesebb hibát eredményez, mint amennyit kapott, akkor az integrációs lépés értékét felére kell csökkenteni, és meg kell ismételni a számításokat.
Példa 1. A négyszögek, a trapézok és a Simpson módszereinek segítségével az Excel-ben egy integrált értéket kell kiszámítani
egy integrációs lépéssel h = 0,25.
A megoldás. A fenti módszerek egyik lehetséges megvalósítását az 1.7. Ábrán (formula megjelenítési mód) és az 1.8-ban (standard mód az Excel-cellák értékeinek megjelenítésére) /
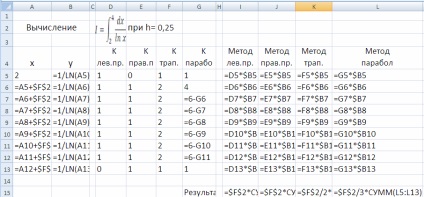
1.7. Ábra - Az integrált számítás Excel munkalapjának töredéke
a képlet megjelenítési módban
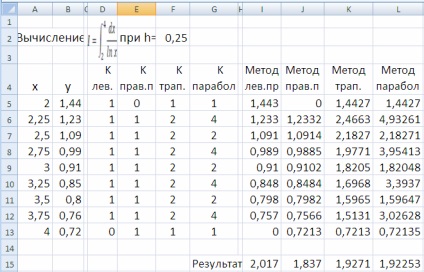
1.8. Ábra - Az Excel táblázatban szereplő töredék, amely az integrált értéket a cellákban megjelenő értékek módjában számítja ki
Az integrálok kiszámításakor a következő képleteket alkalmaztuk:
- a "B2" cellában az "= 1 / LOG (A5)" képletet beírja, és az automatikus kiegészítés segítségével átmásolja a B6-B13 cellákba;
- az "I5" cellába beírja a "= D5 * B5" képletet, amelyet jobbra és lefelé másolunk, hogy kitöltsük az I5: L13 tartományt;
- az "I15" cellába beírja a "= $ F $ 2 * SUM (I5: I13)" képletet, amelyet jobbra az "L15" celláig másolunk;
- a képletben «K15» sejtet adunk a szétválás a integrációs 2. lépés ( «= $ F $ 2/2 * SUM (..."), és a «L15» sejt - Division 3.
Egy példa. Számítsa ki pontosan az integrált értéket # 949; = 0,001.
Az Excel-ben az integrált adatok pontossággal történő kiszámítása a fentiekben ismertetett módszereknél csak a VBA programban végrehajtott kettős számolási módszerrel lehetséges. Egy ilyen program példája az alábbiakban látható.
n = 2 'a partíciók kezdeti száma
Iter = 1-től 100-ig