Optimalizálási probléma
4. fejezet Az optimalizálás matematikai modellei
1. Az f (x) függvény konvexnek mondható, ha legfeljebb a két tetszőleges pontot összekötő szegmensből áll. Egy függvény szigorúan domború, ha teljesen két, tetszőleges, de nem egybeeső pontot összekapcsoló szegmens alatt helyezkedik el.
2. Ha a függvény erősen konvex, akkor egyidejűleg szigorúan konvex és konvex. Ha a függvény szigorúan konvex, akkor egyidejűleg konvex.
3. Egy függvény konvexitása meghatározható a hesseni mátrixból:
· Ha H (x) ³ 0 "x Î R n. akkor a függvény konvex;
· Ha H (x)> 0-x Î R n. akkor a funkció szigorúan konvex;
· Ha H (x) ≥ lE "x Î R n. ahol E az azonosító mátrix, akkor a függvény erős konvex.
Megjegyezzük a konvex funkció fontos tulajdonságát. Ha az f függvény konvex az X halmazon, akkor minden x1 pontnál. x2. xm ÎX és az önkényes nemnegatív számok l1 + l2 +. lm = 1 a következő egyenlőtlenség tartja: Ian Sen
M = 2 esetén ez az egyenlőtlenség egybeesik a konvex függvény definíciójából adódó egyenlőtlenséggel (3.1).
Az optimalizációs probléma önmagában egyszerű és természetes: Az x-re és az x-re definiált x (x) függvényt figyelembe véve meg kell találni az x £ függvény minimális vagy maximális pontját. A minimális feladat a következő:
Ebben az esetben az objektumot objektívnek nevezzük. x egy elfogadható készlet, minden x elem ÎX a probléma elfogadható pontja (4.1.). Ha x egybeesik az egész térrel, a 4.1-es probléma a feltétel nélküli minimalizálás problémájává válik (korlátozás nélkül), egyébként - a feltételes minimalizálás problémájával (korlátokkal).
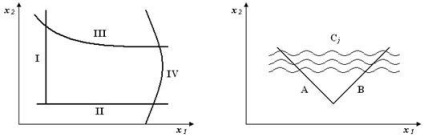
a) lineáris (I, II) és nemlineáris (III, IV) (4.1 ábra);
b) determinisztikus (A.B.) és stasystatic (Cj görbék csoportjai) (4.2.
Ábra. 4.3 Tetszőleges görbe két helyi minima esetén.
Így a globális minimum a legkisebb minden helyi minima. Az 1. ábrán. A 4.3. Ábrán a helyi és a globális minima pontjai láthatóak tetszőleges görbére (x).
Az optimalizálási probléma, amelyben az optimálissági kritérium (x) egyedülálló helyi minimuma az X tartományban, az egy-extremális (unimodális) optimalizációs probléma. A legegyszerűbb unimodális funkciók konvex funkciók (4.4.a ábra).
A 4.4. Ábra egymodális egydimenziós függvényeket mutat be.
Az optimalizációs problémát, amelyben az optimális kritérium f (x) több helyi minima is van, a többszöri optimális probléma.
A legtöbb szélsőséges probléma megoldásának szokásos módszerei biztosítják, hogy csak egy egyedi pontot találjanak, amelyben a részleges származék. Ilyen pont a véletlenszerű körülményektől függően (a kezdeti közelítés választása) lehet bármely helyi minima vagy az inflexiós pont. Ezzel kapcsolatban feltétlenül meg kell vizsgálni azokat a feltételeket, amelyek mellett a megoldás globális minimumot biztosít.
Ha a (4.2) vagy a (4.3) egyenlőtlenség az x # x * -re szigorú, akkor azt mondjuk, hogy x * szigorú minimális (szigorú megoldás) globális vagy helyi értelemben. Nyilvánvaló, hogy a globális megoldás is helyi; a beszélgetés nem igaz.
Annak tükrözése érdekében, hogy az x *ÎX az X. függvény globális minimuma pontjának pontja, a jelölést használjuk:
vagy ezzel egyenértékű rekordot
Azt mondják, hogy az x * pont realizál egy értéket, a £ függvény minimális értéke az X-nél. Az X-re vonatkozó globális minimum | pont összes pontjának halmaza:
Így az Argmin | (x) egyszerűen egy tetszőleges pont a készletből.
Szükség esetén a minimalizálási problémát helyettesítheti a maximalizációs probléma vagy fordítva. Ez azért van így, mert a £ függvény minimális értéke megegyezik a függvény - | függvényével, amelyet az ellenkezőjelgel vettünk, és mindkét szélsőértéket a változók ugyanazon értékeihez érjük el (4.5. Az x * min | (x *) = -max (- | (x *) ponton).
Ábra. Az optimalizálási probléma megfogalmazásához.
Így, ha például a probléma minimalizálása funkció bármilyen korlátozás le akarja cserélni a maximalizációt, elég összerakni a célfüggvény -, hogy megtalálja a maximális ezt a funkciót, és helyette ellentétes előjelű. A kapott érték az eredeti probléma optimális. A (4.1.) Analógiájára feljegyezzük az "X" függvény £ függvényének maximalizálását az alábbi formában:
A problémák (4.1.) És (4.4.), Azaz a Az £ on X függvény minimális és maximális pontját extremum pontoknak is nevezik. és a problémák (4.1.) és (4.4.) szélsőséges problémák.