Grafikonok létrehozása a matlab programozási környezetben
Munkacím: Rajzrajzok a MATLAB programozási környezetben
Terület: Informatika, Cybernetics és Programozás
Leírás: A munka célja: megtanulni a különböző típusú grafikák készítését a MATLAB szoftverkörnyezetben. A programozás alapvető operátorainak tanulmányozása a MATLAB programozási környezetben; elsajátítsák a MATLAB programozási környezet különböző típusú grafikonjainak elveit.
Fájlméret: 354.21 KB
A munkát letöltötték: 31 fő.
Az Orosz Föderáció Oktatási és Tudományügyi Minisztériuma
FGAOU VPO "Belgorod Állami Országos
Kutató Egyetem "(NIU" BelGU ")
SZÁMÍTÓGÉPES TUDOMÁNY ÉS TÁVKÖZLÉSI KAR
INFORMÁCIÓS ÉS TELEKOMMUNIKÁCIÓS RENDSZEREK ÉS TECHNOLÓGIÁK
Jelentés a laboratóriumi munkáról №1
A tudományág számítástechnikájáról
A "Grafikonok létrehozása a MATLAB programozási környezetben"
a 141206-as csoport hallgatója
Petriv Andrey Vladimirovich
Ph.D. Prokhorenko Ekaterina Ivanovna professzor
Cél: megtanulni, hogyan lehet különböző típusú grafikákat készíteni a MATLAB szoftver környezetben.
1) a MATLAB programozási környezetben történő ábrázolás alapvető operátorainak tanulmányozása;
2) elsajátítja a MATLAB programozási környezet különböző típusú grafikonjainak elveit.
Egyéni adatok a munka elvégzéséhez
(opció 17)
1. feladat 1. Hozzon létre egy függvénygrafikont.
Az algoritmus felépítéséhez használt változók:
k 1 - kezdeti x értéke
k 2 az x végső értéke
n az értékek száma
e-lépés (két x érték közötti távolság)
Az 1. feladat diagramja az 1. ábrán látható.
1. ábra.
Az 1. lista az algoritmus végrehajtása a MatLab rendszerben.
k 1 = bemenet ('adja meg a számot');
k 2 = bemenet ('írja be a számot');
n = bemenet ('adja meg a számot');
A szabványos funkciókat itt használjuk
bemenet - adatbevitel
ábra (1), plot (x y) - az 1 grafikus ablakban egy y (x) függvény sima görbéje van, a vektorok dimenzióinak egybe kell esniük
Az algoritmus tesztelése:
Ha k1 = 0; k2 = 1; n = 100 a grafikon a 2. ábrán látható hiperbola ága.
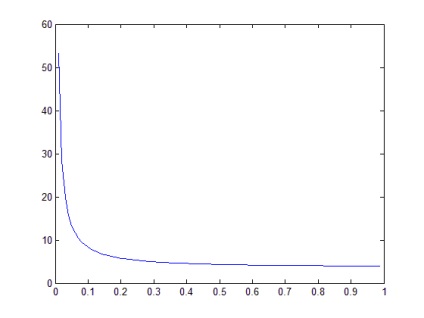
Következtetés: ez az algoritmus lehetővé teszi számunkra, hogy egy adott pontból ábrázoljuk a függvény ábráját.
Hozzárendelés 2. Egy grafikonon 3 görbét hozzon létre: a második kifejezésnek (zöld pont-vonalas vonalnak) megfelelő, első sorban (piros pontozott vonal) felel meg, amely megfelel a hozzáadás eredményének (fekete fázis) (3 periódus).
Az algoritmus felépítéséhez használt változók:
k 1 - kezdeti x értéke
k 2 az x végső értéke
n az értékek száma
e-lépés (két x érték közötti távolság)
y2 (i) # 150; bűn 3 x
y3 (i) # 150; az y1 (i), y2 (i) és az 5. ()
A 2 feladat diagramja a 3. ábrán látható.
3. ábra.
A 2. lista az algoritmus végrehajtása a MatLab rendszerben.
A standard funkciókat itt használjuk:
bemenet - adatbevitel
az (1) ábra; tartsd be; tartsd le # 150; a grafikus ablakban 1, 3 függvénygrafikon készült.
plot (x y 1, '-r') - a grafikus ablakban 1 az y (x) függvény sima görbéje van: egy szaggatott piros vonal jelölő nélkül
(x.y 2, '- .g') - a grafikus ablakban 1 az y (x) függvény sima görbéje: egy zöld dot-dash vonal
plot (x y 3, '- k') - a grafikus ablakban 1 az y (x) függvény sima görbéje van: szilárd fekete vonal jelölő nélkül
Az algoritmus tesztelése:
Ha k1 = 0; k2 = 2 * pi; n = 500 a grafikon a 4. ábrán látható.
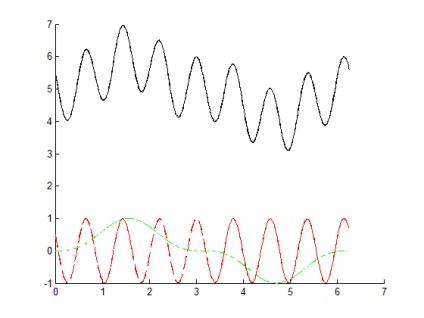
Következtetés: Ez az algoritmus hatékony és lehetővé teszi, hogy egyetlen grafikus ablakban elhelyezni 3 grafikus elszigetelt a maga módján (szaggatott piros vonal nélkül marker zöld vonal pont-kötőjel fekete vonallal nélkül marker ..).
3. feladat: Konstruáljon egy y (x) görbét egy adott reprezentáció alapján.
Epicycloid X = (a + b) cos t - egy cos ((a + b) t / a), y = (a + b) sin t - egy sin ((a + b) t / a). t = [0,2 π) egy> 0 értékre. b> 0, b / a # 150; egy egész szám.
sárga tömör, körtípusjelölővel
Az epicikloid lapos görbe. amelyet a kör állandó pontja alkot. a másik kerület külső oldalán gördülő csúszás nélkül.
Az algoritmus felépítéséhez használt változók:
a kisebb vagy egyenlő b egész szám (egy kisebb kör sugara)
b egy egész szám (egy nagyobb kör sugara)
t 1-kezdeti érték
t 2 végső érték
Az algoritmus folyamatábrája az 5. ábrán látható.
A 2. lista az algoritmus végrehajtása a MatLab rendszerben.
a = bemenet ('adja meg a számot');
b = bemenet ('adja meg a számot');
n = bemenet ('adja meg a számot');
A standard funkciókat itt használjuk:
bemenet - adatbevitel
plot (.. x y „- Oy”) - a grafikus ablakban 1 van kialakítva sima függvény grafikonját y (x): a sárga színű, szilárd összhangban egy markert, például egy kör
Az algoritmus tesztelése:
Ha a = 5; b = 10; n = 500 A grafikon a 6. ábrán látható (lefutás nélküli görbe).
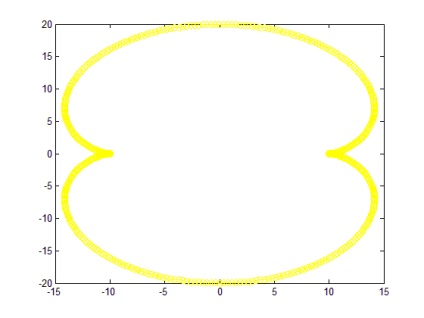
Amikor a és b változik. például a = 2; b = 100 a grafikon módosul, és a 7. ábrán látható.
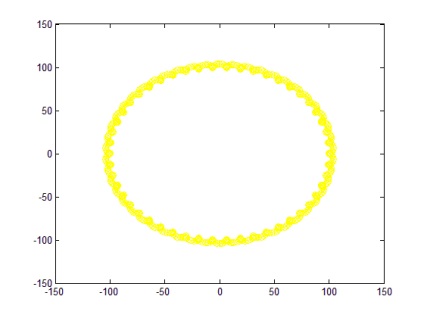
Ha a követelmények nem teljesülnek, akkor a = 5; b = 17; n = 500, a grafikon egy törésformával (8. ábra).
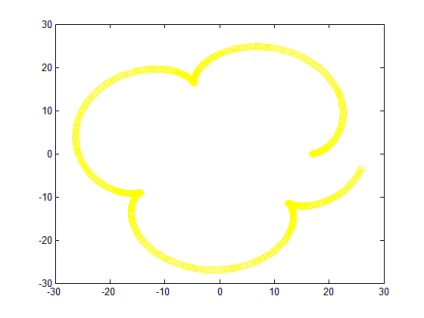
Következtetés: ez az algoritmus lehetővé teszi számunkra, hogy az y (x) görbét egy adott reprezentáció alapján konstruáljuk, a függvény grafikonja elsősorban az a és b értékén alapul. amely megfelel a b / a = egész számnak.
A tanár észrevételei
Közigazgatási bűncselekmény, mint az igazgatási felelősség alapja. A vállalkozói tevékenységet érintő közigazgatási jogsértésekkel kapcsolatos eljárások. Az ügyek anyagi, jogi és eljárási jellemzői a vállalkozói tevékenység területén elkövetett közigazgatási jogsértések esetén.