A mágneses tulajdonságai atomok
ahol # 956; 0 - Bohr magneton, és ez szolgál a mértékegysége atomi vagy molekuláris mágneses pillanatok és számszerűen egyenlő a
Mivel a negatív töltés az elektron, az elektron orbitális mágneses pillanatban van irányítva az ellentétes irányba, hogy a vektor a saját orbitális lendület
Ha az atom van egy külső mágneses mező, például orbitális elektron mágneses pillanat, mágneses momentuma vektorok
l, és a perdület
l fog tekintetében a mágneses mező H meghatározott térbeli helyzetét.
Szerint kvantummechanika, a nyúlvány a vektor
l bármely adott irányban, beleértve az irányt a mágneses mező csak akkor lehet egyenlő
) = H / (2π) · l * · Cos (
Tól (14) és (18) magában foglalja, hogy a kölcsönhatási energia = # 956; l és # 956; S a külső mágneses mező
nagyságrendileg lesz # 916; # 917;
Ezért, H = április 10. E, # 916; # 917;
5 × 10 -5 eV, azaz kölcsönhatási energia # 956; l és # 956; S 4 H
10 Oe kevesebb energiát - kölcsönhatás az alacsony fekvő szinten.
A létezése egy mechanikus (centrifugálás), és a mágneses momentumát az elektron és a magyarázata tulajdonságaik származó relativisztikus kvantummechanika, annak alapegyenletének - Dirac-egyenlet. Különösen, a relativisztikus kvantummechanika a kapcsolatok (15), (16), (17), amelynek érvényessége, mint a létezését centrifugálás megerősítette kísérletek.
A kísérletek megerősítették általában nem önmagában Microsystem mágneses momentuma, és a vetítés. Szerint (17), mint ms =
1/2 néző intrinsic mágneses pillanatban az elektron abszolút értéke egyenlő egy Bohr magneton
Gyakran ez azt jelentette, az érték intrinsic mágneses momentuma az elektron (15), és értékét a nyúlvány (17), és azt mondta, hogy az elektron mágneses momentuma egyenlő nagyságú egy Bohr magneton.
3. §. A teljes mágneses momentuma az egy-elektron atom
Eddig megvizsgáltuk az orbitális viselkedése
S mágneses momentuma az elektron egy külső mágneses mező, feltételezve, hogy nincs kölcsönhatás közöttük. Azonban, annak hiányában a külső mágneses mező ezen pontok között van egy kölcsönhatás, amelyben között kölcsönhatások vannak az orbitális
s pillanatok az elektron (ls - interakció). Ebben az esetben a vektorok
s precessziós mozgást képest vektor teljes lendület
J számszerűen egyenlő
J vannak orientálva egy bizonyos módon viszonyított térben az irányt a mágneses mező, amely az úgynevezett „térbeli kvantálási”.
4.§. Stern-Gerlach kísérlet
A repülő szokásos mágneses mezőt tartalmaz jár nem csak a pillanat erők igyekszik fordítani a mágneses pillanatok tér irányában, hanem cselekedni előfeszítő erő által okozott nem egyenletes mágneses térerősség a pólusok az atomi mágneses dipólus.
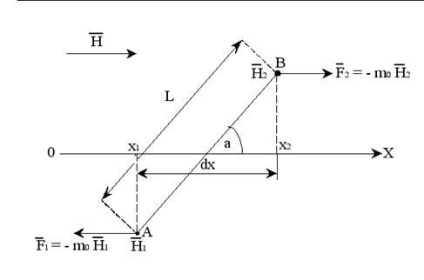
Az m0 - érték „mágneses töltés”, középre az egyes terminálok a atomi mágneses dipólus. H1 és H2 - a mágneses mező intenzitás A és B pontban kifejtett erő a dipól mezőt
az irányba OX, egyenlő FX = F2 - F1 = M0 (H2 - H1) = M0 (dH / dx) dx.
# 956; = M0 L - dipól mágneses momentuma.
Attól függően, hogy a tájékozódás a mágneses momentum (szög # 945;), a dipól elmozdítjuk e mentén az x-tengely (azaz mentén a területen), vagy abba az irányba növekvő mágneses térerősség.
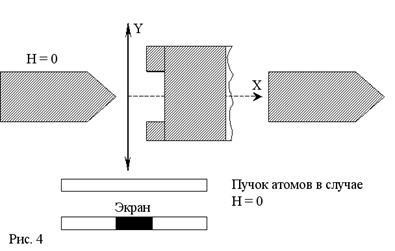
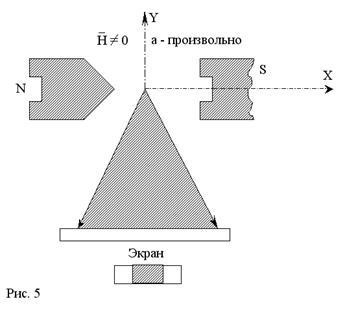
Ha az atomok a mágneses pillanatok, véletlenszerűen orientált a mezőt, akkor a keskeny kezdeti sugár atomok repülő mentén OY tengelye, átkelés az inhomogén mágneses tér mentén OX tengely, feszített egy széles (a villamos tér irányában) csíkot megfelelően tetszőleges értékeket cos # 945; belül
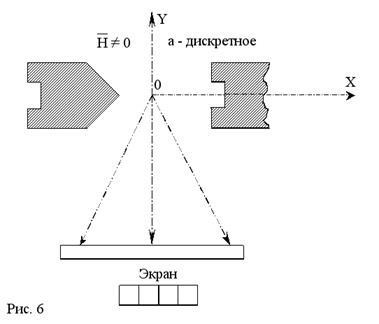
Ha a mágneses pillanatok az atomok is tájolva, a mező irányát az egyetlen meghatározott módon, azaz a cos # 945; csak akkor tud jól meghatározott diszkrét értékeket, összhangban az eredeti gerendát kell bontani a komponensek száma. Mint látható a kimeneti egyenlet (30).
A kísérletek bizonyulhat nemcsak a létezését a mágneses momentum az atom, hanem pontosságát ellenőrizze a következtetéseket az elmélet teret kvantálás.
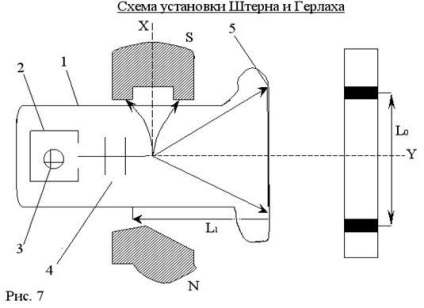
A evakuáljuk nagyvákuumban 1 edényben helyeztük egy kis kemencébe 2, amelyben az ezüst darab 3. Amikor forró sütő elpárologni ezüst, Ag atomok által kibocsátott a kemence minden lehetséges irányban termikus sebességek (
több száz m / sec). Számos rések 4 bocsátanak ki egy keskeny sugár ezüst atomok repülő tengelye mentén Y. A atomi nyaláb repül az régió inhomogén mágneses tér mentén irányul az X tengely A lemezt 5, a gerenda kondenzált rajta. Az atomi sugár oszlik, amely megerősíti a érvényességét térbeli kvantálási elmélet szerint ez létét, atomi mágneses momentuma.
A teljes mágneses momentuma az atom # 956; J = # 956; 0 gj *,
ahol a kvantum száma mJ = j, j - 1, ..., - j.
Minden az ezüst atomok alapállapotú 2 S4. L = 0 orbitális, centrifugálás S = ½, a belső J = ½, Lande faktor
g = 1 + (j (j + 1) + s (k + 1) - l (l + 1)) / 2J (j + 1)) = 2
A mágneses kvantumszám mJ, ha j = ½ mindössze két érték i + ½ és - ½
Következésképpen, csak két lehetséges orientációja mágneses momentuma az ezüst atom az S - mező állapotban van az H.
Oldalról H, a mező szerinti (31) arra kényszeríti, vagy aktus
dx). Ezért néhány atomok irányában mozdul növekvő területen, mások -, hogy csökkentse a feszültséget
, miáltal a gerenda van osztva két komponensek, megerősített kísérletileg.
Ezért, S - állapotban l = 0, akkor # 956; l = 0 (# 956; l = (e / 2MC) Pl), ezért a mágneses momentuma az ezüst atom alapállapotú okozza a belső mágneses momentuma az elektron, és megállapítjuk, 1952 g.
és nem # 956; SH = 2 # 956; MS = 0 # 956; 0. Ez következik a relativisztikus Schrödinger, Dirac-egyenlet. Ez kapott egy különleges nevet - a rendhagyó mágneses elektron. Rendellenes elektron mágneses momentuma miatt kölcsönhatása a saját elektromágneses mezejét.
Ez egy meggyőző kísérleti meglétének igazolása az atomi mágneses momentum és térben kvantálás.
Ha a fényforrás felől nézve merőleges irányban a mágneses mező (az Y tengely mentén), minden egyes sor osztott és három részből áll:
# 957; 0; # 957; 0 + # 916; # 957 ;; # 957; 0 - # 916; # 957 ;; ahol # 957; 0 - vonal jelentése hiányában a mágneses mező;
# 916; # 957; 0 = eH / 4πmC;
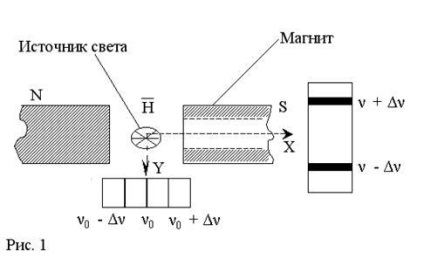
H - intenzitása a külső mágneses mező.
Ha a fény nézett végig az irányt a mágneses mező
(Az X tengely mentén), amelyek mindegyike osztja csak két komponenst
A hiányában a mágneses mező az atom olyan állapotban van, az energia EY. Tedd egy külső erőtérben