típusú grafikonok
Bármely rendszer feltételezi jelenlétében diszkrét állapotok, vagy a jelenléte csomópontok és a közöttük lévő átmenetek leírható egy grafikon. Csomópontok közötti kapcsolatok (V) gráf nevezett élek (E). Ha a gráf pontjai nincsenek számozva, az élek irányítatlan. Egy grafikont csomópontok számozott bordák vannak irányítva, és az úgynevezett ívek
(Ábra. 2).
Pontpár lehet csatlakoztatva két vagy több bordát (ívek), az ilyen éleket (ívek) nevezzük többszörös. Csúcsok összekötve egy él (ív) nevezzük szomszédos. Ha a széle kezdődik és végződik ugyanabban az vertex nevezzük hurok.
Az élek száma áradó vertex vi (hurok kétszer számolja), az úgynevezett vegyérték (fokú csúcsok) jelöljük: d (vi).
Ha V és E véges halmazok, akkor a megfelelő grafikon azt mondják, hogy véges. A grafikon az úgynevezett degenerált. ha nincs élek.
Irányítatlan gráf hívják egyszerű. ha nincs hurkok, és bármely két csúcsot köti össze legfeljebb egy él. A grafikonok jelennek meg a gépen egy sor pontok és az azokat összekötő vonalak vagy vektorokat. Az arcok jelennek meg, és a görbe vonalak, ezek hossza nem számít. Egy gráf sík (lapos). ha meg lehet jeleníteni keresztezése nélkül néz szembe a síkban (5.). Egy gráf van csatlakoztatva. ha bármely két csúcsa van egy sorozat élek őket összekötő (3.), azaz gráf nem izolált fragmenseket (csúcsok, élek). Egy gráf teljes. ha bármely két pont között csak az egyik él (4. ábra). Ha egy teljes gráfnak n csúcsú, az élek számát egyenlő n (n-1) / 2. Speciális típusú gráf egy fa (6.), A gyűrű és a listák, amelyek nem szerepelnek a felülvizsgálat a mi természetesen.
Gróf amelynek minden csúcsa van egyforma mértékben egy reguláris gráf.
ugyanazon sor tárgyak gyakran határozza meg számos különböző bináris kapcsolatok. Képviselni egy ilyen helyzetben vannak multigráfokra. Multigráfokra fogják használni, hogy képviselje a diagramok a véges automaták.
Egy él (arc) és minden csúcsához nevezzük esemény. Azt mondjuk, hogy (arch) (u. V) összeköti csúcsok u és v. Ha a vertex nem esemény bármelyike él (ARC), akkor azt mondják, hogy izoláljuk (d (vi) = 0), ha tartozik, hogy csak az egyik él (ív), majd az úgynevezett lóg (d (vi) = 1).
A főbb rendelkezések az a gráf:
1. A G gráf összege fok minden csúcs - páros kétszeresével egyenlő az élek száma, mivel minden él ezen összeg egy részéből pontosan kétszer. Ez az eredmény az úgynevezett kézfogás lemma: ha több ember kezet, akkor a teljes kézfogások száma sőt szükséges, mert minden kézfogás jár két kéz (mindkét kézzel számít, ahányszor részt vett a kézfogás).
2. A páratlan számú csúcsainak minden gráf páros.
3. minden gráf n csúcsú, ahol n ³2, mindig vannak legalább két csúcsú egyenlő hatalmat.
4. Ha egy gráfot csúcsot n> 2 két csúcsot azonos mértékű, ez a rajzon látható mindig van vagy egyik csúcsa fokú 0, vagy egyik csúcsa mértékben n - 1.
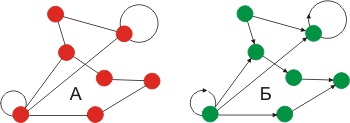
Két grafikonok G1 = (V1, E1) és G2 = (V2, E2) nevezzük izomorfak. ha közötti csúcsok létezik egy az egyhez megfelelés.
izomorfizmus két grafikon algoritmus G1 (X, E) és G2 (Y, E)
1. Ha X ≠ Y, a grafikonok nem izomorfak.
2. levelet ki az összes elemet egyaránt grafikonok, meghatározzuk a pár (xi, xj) és (yi. Yj) minden egyes elem, ahol xi. yi - az esetek száma minden csúcsa a két gráf és xj. yj - a bejegyzések száma.
3. Minden olyan elem x a grafikon G1 keres egy elem y a grafikon G2. hogy az a feltétel: a számos eredmények x egybeesik száma eredmények y, és x bejegyzések száma egyenlő a bejegyzések száma y. Talált elemek x és y összekapcsolják ív, azaz Mi megépíteni a megfelelő grafikon. Ha nincs egyezés, akkor az izomorf gráfok.
4. Mi írjuk a helyettesítés, ami lefordítva grafikon G1 G2 gráf.
Példák hozzárendelések