Az elmélet a gráfizomorfizmus
Count létezhetnek különböző formái, amelyek azonos számú csúcsok, élek, és a szélei ugyanazon vegyület. Az ilyen grafikonok nevezzük izomorf grafikonok. Vegye figyelembe, hogy hívjuk grafikonok ebben a fejezetben elsősorban abból a célból utal rájuk, és felismerte őket egymástól.
izomorf gráfok
Két grafikont G 1 és G 2 izomorfak. ha -
- Ezek mennyisége a komponensek (csomópontok és élek) azonos.
- Kapcsolatuk szélén megmarad.
Megjegyzés - Röviden, a gráfok izomorfak egymással adaptált változata. Jelöletlen grafikon is tekinthető, mint egy izomorf gráf.
A mértékű szekvencia G 1 és G 2 azonosak.
Ha vertex 1, V 2,. V k> ciklust képeznek K hosszú, hogy G 1, akkor a felső 1), F (V 2),. F (V k)> K kell képeznie, egy ciklus hosszúságú G 2.
Az összes fenti feltételek szükségesek G 1 és G 2 izomorfak, de nem elég. bizonyítani. hogy a grafikonok izomorf.
(G 1 ≡ G 2), ha és csak akkor, ha. ha (G 1 - ≡ G 2 -). ahol G 1 és G 2 egyszerű grafikonok.
(G 1 ≡ G 2). Ha a szomszédsági mátrix G 1 és G 2 azonosak.
(G 1 ≡ G 2), ha és csak akkor, ha. adott esetben részgráfok G 1 és G 2 (eltávolításával kapjuk meg néhány, a csúcsok a G 1 és a képeket a G gráf 2) izomorfak.
Az alábbiak közül melyik gráfok izomorfak?
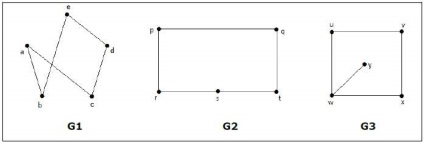
G oszlop 3. csúcs „W” csak egy bizonyos 3, míg az összes többi csúcs foka 2. ezért. 3. G nem izomorf G 1 vagy G 2.
Figyelembe kiegészítők G 1 és G 2, akkor -
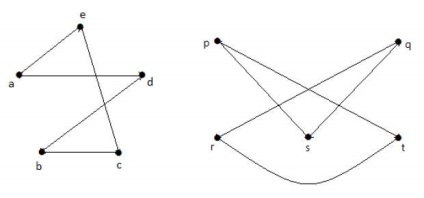
síkgráfok
„G” gráf nevezzük sík, ha lehet levonni egy síkban vagy gömb úgy, hogy nincs két szélét metszik egymást a ponton, nem a tetején.
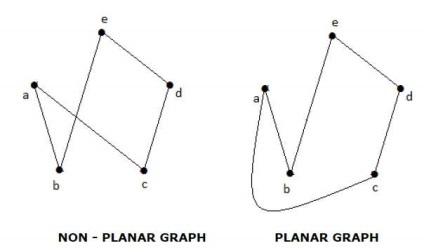
Minden sík grafikon osztja a síkot csatlakoztatott régiók, az úgynevezett régiókban.
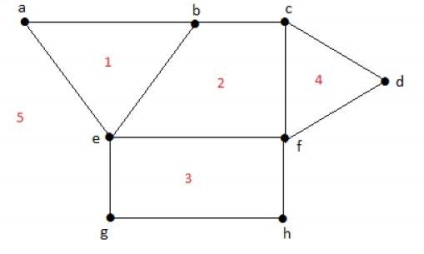
Képzés korlátozott oblastig = deg (r) = élek számát környező régiók
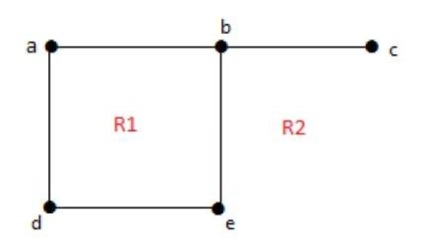
A mértéke korlátlan oblastig = deg (r) = élek számát környező régiók
A síkgráfok a következő tulajdonságokkal rendelkezik egy jó hely -
1. A síkbeli gráf „N” csúcsok, az összege fok minden csúcs
n Σ = 1 ° (V r) = 2 | E |
2. Összhangban az összege fok a régióban a tétel, egy síkban gráf „n” nak, az összeget a hatáskörét a régiók -
n Σ = 1 ° (R g) = 2 | E |
A fentiek alapján tétel, levonhatjuk az alábbi következtetéseket -
A sík gráf,
Ha a mértéke minden terület K, az összeget a fokozatok régiók
Ha a mértéke az egyes régiók, legalább K (≥ K), majd a
Ha a mértéke minden terület kevesebb, mint K (≤ K), az
Közlemény - Tegyük fel. hogy minden régió ugyanolyan mértékben.
3. Összhangban a Euler képlet síkgráfok
Ha a gráf „G” jelentése egy csatlakoztatott lapos, majd
| V | + | R | = | E | + 2
Ha egy sík gráf komponenseinek „K”, a
| V | + | R | = | E | + (K + 1)
Ahol | V | a csúcsok száma, | E | az élek számát, és | R | a régiók számát.
4. Border Vertex egyenlőtlenség
Ha a „G” jelentése egy csatlakoztatott síkbeli gráf a mértéke minden egyes területen legalább, „K”, akkor,
Tudod, | V | plusz; | R | = | E | plusz; 2
K (| E | - | V | plusz; 2) ≤ 2 | E |
(K - 2) | E | ≤ K (| V | - 2)
5. Ha a „G” jelentése egy egyszerű csatlakoztatott sík gráf, akkor
Létezik legalább egy v ∈ G, úgy, hogy a mértéke (V) ≤ 5
6. Ha a „G” jelentése egy egyszerű gráf csatlakoztatott lapos (legalább két él), és anélkül, háromszögek, majd
Tétel 7. Kuratowski-
„G” A gróf nem sima, akkor és csak akkor, ha. amikor a „G” részgráfja homeomorf K 5 vagy K 3.3.
homomorfizmus
Két grafikont G 1 és G 2 nevezzük homomorf, ha minden egyes ilyen grafikonok lehet származhatnak ugyanabból gráf „G”, G elválasztó néhány bordák nagy a csúcsok száma. Tekintsük a következő példát -
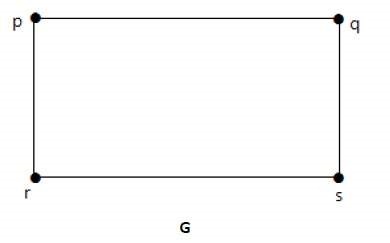
Osszuk a szélén a „RS” a két szélén, hozzátéve, egy csúcsot.
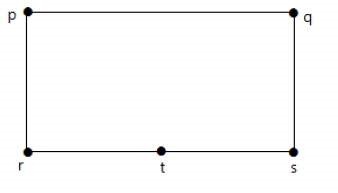
Alábbi grafikonon homomorfikus első grafikon.
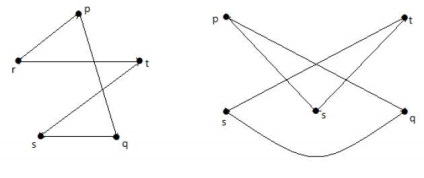
Ha G 1 izomorf G 2 G homeomorf G 2, de a fordított nem szükségszerű.
Bármely gráfot négy csúcsot kevésbé lapos.
Bármely grafikon 8 vagy kevesebb ig lapos.
Komplett gráf K n lapos, ha, és csak akkor, ha. amikor n ≤ 4.
A teljes páros gráf K m, n lapos, ha, és csak akkor, ha. ha m vagy n ≤ 2 ≤ 2.
Egyszerű nem síkbeli gráf minimális csúcsok száma egy teljes gráf K 5.
Egyszerű nem síkbeli gráf a minimális számú élek K 3, 3.
sokrétű menetrend
Egyszerű csatlakoztatott sík gráf nevezzük poliéderes grafikon, ha a minden csúcsa ≥ 3, azaz ° (V) ≥ 3 ∀ V ∈ G.