Gauss-eloszlás
SV Usatikov, PhD a fizika és a matematika, egyetemi docens; SP Hrushevsky, PhD a fizika és a matematika, egyetemi docens; MM Kirichenko, kandidátusa Társadalomtudományok
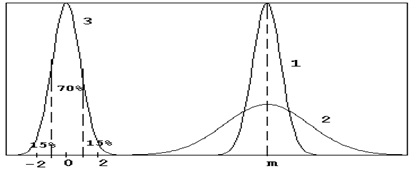
1. ábra sűrűségfüggvénye a szokásos gyakorlat
1.2 - menetrendek egy átlag m, és a standard eltérés a különböző s. ahol s 1
3 - A grafikon és m = 0, s = 1, Z - példakénti eloszlását jog és a görbe alatti terület.
Kevesebb érv x ide kell érteni a különböző számértékek hogy nem lehet előre a kísérlet megkezdése előtt: magasság, súly, a hibák száma a tesztelés során, szellemi fejlődés, a bűnözés és minden más felmerülő eredményeként kívül számos független (vagy gyengén függő) és összehasonlítható az, hogy a befolyása a véletlen hatások. A f (x) az alábbi fontos információkat: egy x számszerű értékkei a valószínűsége, hogy egy nagyobb értékre, mint a szám, és kisebb számú egyenlő a görbe alatti terület f (x), az [a, b] (1. ábra). Természetesen ez vonatkozik minden a és b között egy közeli vagy távoli, bárhol a sorban x. Továbbá, a terület alatt a teljes görbe f (x) jelentése 1, azaz a a valószínűsége, x, hogy a vonal értéke 1, és ez az esemény jelentős (ez a funkció is nevezik a normalizációs feltétel).
Normális törvény két paraméter teljesen meghatározza azt: a számok m és s. Az m szám az átlagos érték összegek érdekes számunkra: az átlagos magasság, átlagos tömeg stb Változtatásával m. t végezhet párhuzamos eltolása a görbe f (x) az x tengely mentén. Az is látható, hogy a legvalószínűbb előfordulási x A kísérletben közel m. alatti terület f (x) bármely szegmens tartalmú m, legnagyobb.
A s számot az átlagos eltérés a numerikus index x az m szám: kisebb, mint s. A „meredekebb” válik a „hegy” f (x) (1. ábra), és a kevésbé valószínű, hogy nagyon különbözik x m. Ezzel szemben, a nagy s „Hill” f (x) terjed át a „sima” és szinte azonos valószínűséggel, úgy tűnhet, mint egy közeli m. és önkényesen messzire m.
Ha a numerikus index x számítani száma Z a következő szabály szerint:
az összes „a hegyek” f (x) pedig egy görbe Z törvény 3. Gauss az 1. ábrán. Ezután az összes pontot ± 1 megfelel rámutat Z m ± s x, egy pontot ± 3 Z - m ± 3s pont x. Az elosztó a görbe alatti területek 3. azt mutatja, hogy a intervallum [-3,3] koncentráljuk körülbelül 99,7% a teljes görbe alatti terület f (x). Ezért az úgynevezett szabály „három s” törvény Z: p valószínűséggel = 0,997 véletlen értéket x eltér az összes „hegyek” f (x) lesz egy görbét 3 törvény Z az 1. ábrán. Ezután az összes pontot az átlag ± 1 m (balra vagy jobbra) nem több, mint 3 mp.
Most elérkezett az idő, hogy miért olyan nagy hangsúlyt a „hegy” f (x) az 1. ábrán. A valószínűségszámítás, a tétel bizonyított joggal nevezik a központi határeloszlás tétel. A durva kifejezéseket, az összeg nagy számú (közel több mint 7-10) független valószínűségi változók, amelyek hasonlóak ahhoz a hatásukat a diszperziós tárgyát képező összeget a szokásos gyakorlat. Például a magassága egy ember, ami számos tényező befolyásolja, melyek közül a tömege nem domináns befolyását.
Ez bebizonyította, hogy nagyon hasznos bevezetés a törvény Pearson c 2 (2. ábra) Mivel az elején a huszadik században a biztosítási üzlet, hogy tisztázza a kereskedelem kereslet és népszerűsége a politikusok, stb
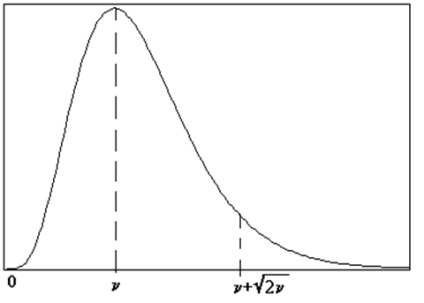
2. ábra. valószínűségi sűrűség zakonac 2, n szabadsági fokkal.
Az érv x definiált itt összegeként n független változók a négyzet, amelyek mindegyike a szokványos Z- törvény m = 0, és s = 1. Egyértelmű, hogy nagy n (gyakorlatilag n> 30) törvény c 2 átalakítjuk egy szokásos törvény m = n és s =
, Úgy viselkedik, mint Ljapunov-tétel. Gyakran azonban a feltételek nem több, mint 10. Az n szám száma szabadsági fokkal. A jelentése az f (x) jelentése ugyanaz, mint a normál törvény: a valószínűsége, hogy egy adott x numerikus értékre = c 2 esik egy előre meghatározott tartományon egyenlő a görbe alatti terület f (x). Így a görbe alatti terület az intervallum 0 és n +
Ez több, mint 90% -a alatti terület a teljes görbe f (x). Ezért kell tartózkodnia szabály „három s” törvény C 2 valószínűséggel 0,9 PI véletlen változó X = C nem haladja meg a 2 n + C 2n (nyilván, c 2 nem lehet negatív).
Végül említést kell tenni törvény Student-féle t nyerünk normál jog és zakonac 2. A valószínűségi változó t kapunk abból a frakcióból, amelyben a számlálóban a Gauss valószínűségi változó Z m = 0, és s = 1, és a nevező - véletlenszerű c 2 érték n fok szabadság. Szerint -prezhnemu nagy n Law Student megy a rendes törvény (majdnem n i 30). De még a kis n típusú valószínűségi eloszlást görbe t nagyon hasonló a 3. görbe 1. ábra. A különbség az, hogy ahelyett, hogy s = 1 Z kell venni s = n / (n -2), t.e.srednee eltérés a t m = 0 nagyobb, mint az átlagos eltérés a Z m = 0. Ennek megfelelően a „hegy” Törvény t laposabb, mint a „hegy” a törvény Z.
Minden anyag a „Matematika”